Coursera ML week1 综述&梯度下降
week 1
What is machine learning?
课程中给出了两个定义:
1:Arthur Samuel (1959). Machine Learning: Field of study that gives computers the ability to learn without being explicitly programmed.
这个是一种更久远的定义,Arthur Samuel将其定义为 “给予计算机能自我学习的能力而不是编程”
2:Tom Mitchell (1998) Well-posed Learning Problem: A computer program is said to learn from experience E with respect to some task T and some performance measure P, if its performance on T, as measured by P, improves with experience E.
这一个更新的定义是Tom Mitchell 提出的,“对于某类任务T和性能度量P,如果一个计算机程序在T上以P衡量的性能随着经验E而自我完善,那么我们称这个计算机程序在从经验E学习。”
Machine learning algorithms
机器学习算法的分类主要是监督学习,无监督学习和其他的一些算法:
1:Supervised learning(监督学习)
2:Unsupervised learning(无监督学习)
3: Others: Reinforcement learning, recommender systems.
Supervised Learning
通过已有的训练样本来训练,得到一个最优的模型,利用这个模型可以将新的数据输出相应的值。
监督学习分为“回归”(regression)和“分类”(classification)。
回归问题:预测一个连续的值。
分类问题:预测一个离散的值。
Unsupervised Learning
在监督学习中,我们明确的知道我们需要的结果是什么,但在无监督学习中,我们是不知道产生的结果是什么的。
在无监督学习中,我们只有一个数据集,聚类算法可以将一个数据集分成多个聚集簇。当然,无监督学习还有其它算法。(具体的实现过程会在后面的课程中讲到)
列如聚类:收集1,000,000个不同的基因,并找到一种方法,将这些基因自动组合成相似或相关的不同变量,如寿命、位置、角色等。

Cost funcion(代价函数)
代价函数在我的理解中是使的目标函数最优

我们需要的是为上面这个模型选择合适的参数θ0和θ1 ,使其误差最小。
而我们需要的是让误差最小,即目标函数最优解。也就是求下面J函数的最小值。

学习算法的优化目的是找到一个最优的θ1,使的J(θ1)最小化。
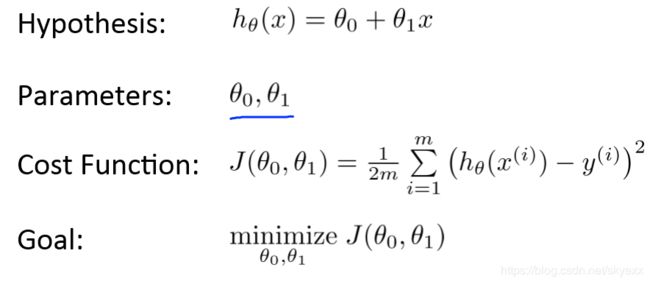
这就是cost function的三维图像: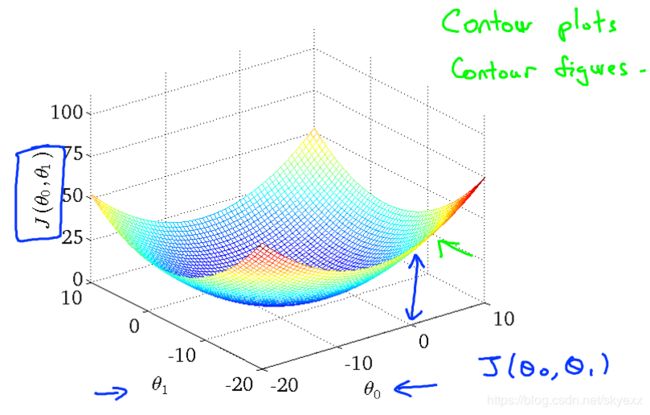 也可以在二维图种用轮廓图代替:
也可以在二维图种用轮廓图代替:


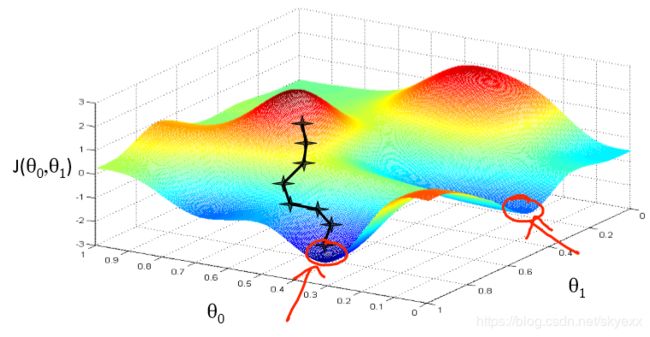
Gradient descent(梯度下降法)
梯度下降法可以让代价函数J得到最优化
 假设只有两个θ,当然多个也是一样的。先初始化θ0=θ1=0,然后每次都往θ0,θ1下降最快的方向移动,不停的改变θ0和θ1的值,最后就可以得到最小值了。当然也可能是局部最小。
假设只有两个θ,当然多个也是一样的。先初始化θ0=θ1=0,然后每次都往θ0,θ1下降最快的方向移动,不停的改变θ0和θ1的值,最后就可以得到最小值了。当然也可能是局部最小。
可以想象成你在山顶,你想以最快的步伐到山地,看到每次都是往斜度最大的方向走,梯度下降法也是类似的。

α表示学习率,它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。θ0,θ1必须同步更新,不然会出错。

如果α大小,结果是它一点一点的挪动,非常的缓慢,需要很多步才能到达全局最低点。
如果α太大,那么梯度下降法可能会越过最低点,甚至可能无法收敛乃至发散。知道你发现实际上离最低点越来越远。

当只有一个参数时我们可以看成,先初始化θ1的值,然后用梯度下降法一步一步往下移,当越接近最低点时,导数就越小,那么幅度也越接近0,直到等于0时θ1的值将不会被改变。
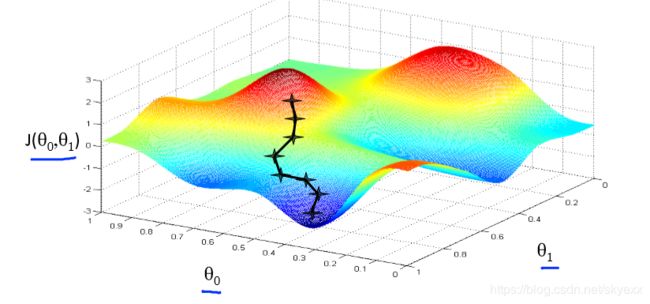
Gradient descent for linear regression
用梯度下降法运用在平方误差代价函数中,下图是梯度下降法和线性回归算法的比较:
 想要最优化J(θ0,θ1),就要不断的改变θ0,θ1的值。直到J(θ0,θ1)收敛。J(θ0,θ1)的导数如下:
想要最优化J(θ0,θ1),就要不断的改变θ0,θ1的值。直到J(θ0,θ1)收敛。J(θ0,θ1)的导数如下:
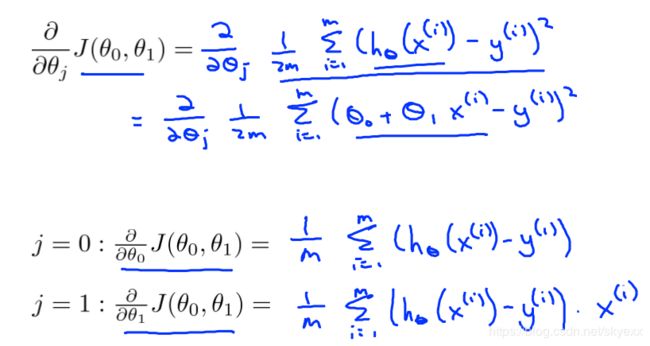
梯度下降就变成了:
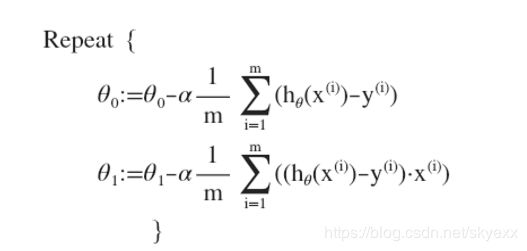
执行梯度下降时,根据你的初始值的不同,可能会得到不同的局部最优解。