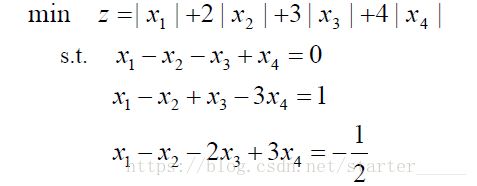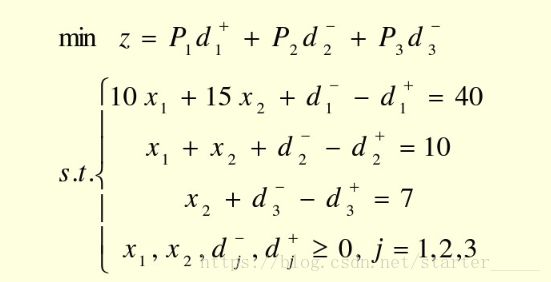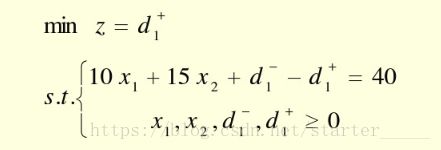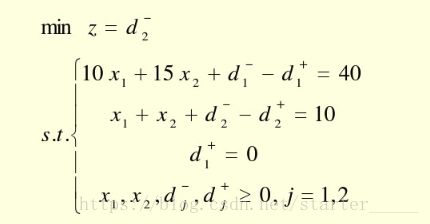Lingo —— 求解规划问题

---

线性规划

（1）定义：线性规划问题是在一组线性约束条件的限制下，求一线性目标函数的最优解的问题。

（2）举例：

model:
    min=@abs(x1)+2*@abs(x2)+3*@abs(x3)+4*@abs(x4);! 目标函数;

    x1-x2-x3+x4=0;
    x1-x2+x3-3*x4=1;
    x1-x2-2*x3+3*x4=-1/2;! 约束条件;
end

---

非线性规划

（1）定义：非线性规划问题是在一组非线性约束条件的限制下，求一非线性目标函数的最优解的问题。

（2）举例：

model:
    min=(x1)^2+(x2)^2+8;! 目标函数;
    x1^2-x2>=0;
    -x1-x2^2+2=0;
    x1>=0;
    x2>=0;! 约束条件;
end

---

整数规划

（1）定义

规划中的变量（部分或全部）限制为整数时，称为整数规划。若在线性规划模型中，变量限制为整数，则称为整数线性规划。

（2）分类

如不加特殊说明，一般指整数线性规划。整数线性规划模型可划分为：

1. 纯整数线性规划：所有变量限制为整数
2. 混合整数线性规划：部分变量限制为整数

（3）举例

model:
    sets:
        row/1..4/:b;!四个不等式;
        col/1..5/:c1,c2,x;!五个未知数x;
        link(row,col):a;!a是x对应的系数;
    endsets
    data:
        c1=1,1,3,4,2;
        c2=-8,-2,-3,-1,-2;
        a=1 1 1 1 1
        1 2 2 1 6
        2 1 6 0 0
        0 0 1 1 5;
        b=400,800,200,200;
    enddata
max=@sum(col:c1*x^2+c2*x);! 目标函数;

@for(row(i):@sum(col(j):a(i,j)*x(j))@for(col:@gin(x));
@for(col:@bnd(0,x,99));! 约束条件;

end

---

动态规划

（1）定义：

动态规划主要用于求解以时间划分阶段的动态过程的优化问题。动态规划是求解某一类问题的一种方法，是考察问题的一种途径，而不是一种特殊的算法（如线性规划是一种算法），因此，它不像线性规划一样有一个标准的数学表达式和明确定义的一组规则，而必须针对具体情况具体分析。

（2）举例：

model:
    sets:
        vertex/A,B1,B2,C1,C2,C3,C4,D1,D2,D3,E1,E2,E3,F1,F2,G/:L;
        road(vertex,vertex)/A B1,A B2,B1 C1,B1 C2,B1 c3,B2 C2,B2 C3,B2 C4,
        C1 D1,C1 D2,C2 D1,C2 D2,C3 D2,C3 D3,C4 D2,C4 D3,
        D1 E1,D1 E2,D2 E2,D2 E3,D3 E2,D3 E3,
        E1 F1,E1 F2,E2 F1,E2 F2,E3 F1,E3 F2,F1 G,F2 G/:D;
    endsets
    data:
        D=5 3 1 3 6 8 7 6
        6 8 3 5 3 3 8 4
        2 2 1 2 3 3
        3 5 5 2 6 6 4 3;
        ! D是每条路的长度;
        L=0,,,,,,,,,,,,,,,;
        ! L是总路径;
    enddata
@for(vertex(i)|i#GT#1:L(i)=@min(road(j,i):L(j)+D(j,i)));
end

---

目标规划

（1）引言

1. 线性规划的局限性：只能解决一组线性约束条件下，某一目标只能是一个目标的最大值或最小值的问题
2. 实际决策中，衡量方案优劣要考虑多个目标

（2）定义

目标规划是一种用来进行含有单目标和多目标的决策分析的数学规划方法。它是在线性规划基础上发展起来的算法。

（3）相关概念

1. 正、负偏差变量：

   设d为决策变量的函数，正偏差变量 d+=maxd−d0,0 d + = m a x d − d 0 , 0 ，表示决策值超过目标值的部分，负偏差变量 d−=−mind−d0,0 d − = − m i n d − d 0 , 0 ，表示决策值未达到目标值的部分，这里 d0 d 0 表示d的目标值。因决策值不可能同时超过目标值又未达到目标值，故恒有 d+∗d−=0 d + ∗ d − = 0

2. 绝对约束和目标约束：

   绝对约束是指必须严格满足的约束，如线性规划中的约束条件；目标约束是目标规划特有的约束，线性规划问题的目标函数，在给定目标值和加入正、负偏差变量后可变换为目标约束。

3. 优先因子（优先等级）与权系数：

   一个规划问题如果有多个目标，可以按照重要性来规定一个优先因子P，越重要的越优先。

4. 目标规划的目标函数

   目标规划的目标函数是按各目标约束的正、负偏差变量和赋予相应的优先因子而构造的。当每一目标值确定后，决策者的要求是尽可能缩小偏离目标值。

   a. 要求恰好达到目标值，即正负偏差都要小： min m i n z=f(d++d−) z = f ( d + + d − )

   b. 要求不超过目标值，正偏差小： min m i n z=f(d+) z = f ( d + )

   c. 要求超过目标值，负偏差小： min m i n z=f(d−) z = f ( d − )

（4）类型：

1. 加权系数法：为每一个目标加一个权系数，把多目标模型转化成单一目标模型。但是困难时确定合理的权系数，以反映不同目标之间的重要程度。

2. 优先等级法： 将各目标按其重要程度分为不同的优先等级，转化为单目标模型。

3. 有效解法：寻求能够照顾到各个目标，并使决策者感到满意的解。由决策者来确定选取哪一个解，即得到满意的解。但是有效解太多，无法挑选

（5）举例（Lingo不能直接求解目标规划问题，但可以通过逐级求解线性规划的方法，求得目标规划问题的解）：

题目：

首先，对应第一优先级建立线性规划问题。（其中，d1_代表 d1− d 1 − ，d1代表 d1+ d 1 + ）

model:
    min=d1;
    10*x1+15*x2+d1_-d1=40;
end

解得 d1+ d 1 + =0，将 d1+ d 1 + =0作为约束条件，对应第二优先级建立线性规划问题

model:
    min=d2_;
    10*x1+15*x2+d1_-d1=40;
    x1+x2+d2_-d2=10;
    d1=0;
end

解得 d2− d 2 − =6，将 d1+ d 1 + =0， d2− d 2 − =6作为约束条件，对应第三优先级建立线性规划问题

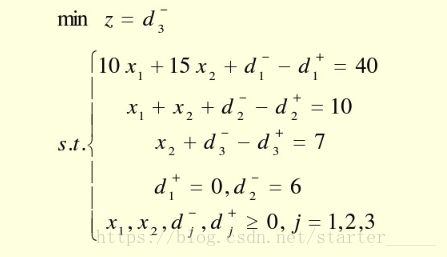
model:
    min=d3_;
    10*x1+15*x2+d1_-d1=40;
    x1+x2+d2_-d2=10;
    x2+d3_-d3=7;
    d1=0;
    d2_=6;
end

最终，得最优解为 x1=4,x2=0,d1+=0,d2−=6,d3−=7 x 1 = 4 , x 2 = 0 , d 1 + = 0 , d 2 − = 6 , d 3 − = 7 ，最优值为7