预测海藻数量(R语言)

1. 问题描述与目标
我希望通过建立预测模型预测河流中有害海藻的数量。本案例的目的是更好地了解影响藻类频率的因素。也就是说，我们要了解藻类的频率和水样的某些化学性质以及其他特征(如季节、河流类型等)是如何相关的。

2. 数据说明
有两个数据集，第一个数据集有200个水样。该数据集的每一条记录是同一条河流在该年的同一个季节的三个月内收集的水样的平均值。
每条记录由11个变量构成。其中3个变量是名义变量，它们分别描述水样收集的季节、收集河流的大小和河水速度。余下的8个变量是所观察水样的不同化学参数，即最大pH值、最小含氧量（O2）、平均氯化物含量(cl)、平均硝酸盐含量(NO3)、平均氨含量(NH4)、平均正磷酸含量(PO4)、平均磷酸盐含量(PO4)、平均叶绿素含量。与这些参数相关的是7种不同有害藻类在相应水样中的频率数目。并未提供所观察藻类的名称的有关信息。

第二个数据集由140个额外观察值构成。它们的基本结构和第一个数据集一样，但是它不包含7种藻类的频率数目。本案例的主要目的是预测140个水样中7种藻类的频率。

在这种问题中，任务是建立预测模型，并预测在给定预测变量的取值时相应的目标变量的值。预测模型也可能会说明哪一个预测变量对目标变量有较大的影响，即模型可能提供影响目标变量因素的一个综合描述。

3. 数据加载到R
两种方法：1)利用提供的R添加包；2)下载相应数据的文本文件，然后把文件读入到R中

第一种方法：安装R添加包，该添加包提供了案例的数据集和函数，代码如下：install.packages(‘DMwR’) 只要载入了R添加包，就直接有了一个名为algae的数据框。这个数据框含有前面提到的200个观测值:

>library(DMwR)
>head(algae)

数据框可以看做一种有列名称的矩阵或者表格。函数head()将显示数据框的前6行。

第二种方法：先从网站http://www.dcc.fc.up.pt/~ltorgo/DataMiningWithR/下载三个文本文件。“Analysis.txt”中包含200个水样，而”Eval.txt”中包含140个测试样本。“Sols.txt”包含140个测试样本的藻类频率。将文本文件读入到R中的代码如下：

>algae <- read.table('Analysis.txt',
          header=F,
          dec='.',
          col.names=c('season','size','speed','mxPH','mnO2','Cl',
          'NO3','NH4','oPO4','PO4','Chla','a1','a2','a3','a4',
          'a5','a6','a7'),
          na.strings=c('XXXXXXX'))

参数header = F表示要读的文件的第一行不包括变量名。dec=’.’指出数值使用’.’字符分隔小数位。这两个参数设置可以省略，因为这里使用了它们的默认值。

4. 数据缺失
当我们处理含有缺失值的数据时，可以有几种处理策略：
1.将含有缺失值的案例剔除
2.根据变量之间的相关关系填补缺失值
3.根据案例之间的相似性填补缺失值
4.使用能够处理缺失值数据的工具

4.1 将缺失部分剔除
剔除含有缺失数据的记录非常容易实现，尤其当这些记录所占的比例在可用数据集中非常小的时候，这个选择就比较合理。

在剔除某些变量中至少含有一个缺失数据的所有观测值时，最好先检查观测值，或者至少得到这些观测值的个数，例如：

>algae[!complete.cases(algae),]

函数complete.cases()产生一个布尔值向量，该向量的元素个数与algae数据框中的行数相同，如果数据库的相应行中不含NA值(即为一个完整的观测值)，函数返回的值就是TURE。

当然我们也可以用如下代码统计不完整数据的个数：

>nrow(algae[!complete.cases(algae),])
[1] 16

除了统计个数之外，我们还可以删除这16条不完整数据的样本:

>algae <- na.omit(algae)

几个处理NA数据很有用的函数：
na.fail 返回不包含缺失值记录的数据
na.omit 返回剔除了缺失值记录的数据
na.pass 返回没有作任何处理的数据

即使我们不适用剔除所有包含缺失值记录的极端方法，我们也可以剔除某些缺失值太多的样本，这些样本几乎是无用样本，如果采用复杂的方法来填补缺失值，就会导致较大偏差。我们观察这16个缺失值记录的数据，可以看到62条和199条记录中的11个解释变量有6个是缺失值。

    season   size  speed mxPH mnO2    Cl   NO3 NH4    oPO4     PO4  Chla   a1   a2  a3   a4  a5  a6  a7

62  summer  small medium 6.40   NA    NA    NA  NA      NA  14.000    NA 19.4  0.0 0.0  2.0 0.0 3.9 1.7

199 winter  large medium 8.00  7.6    NA    NA  NA      NA      NA    NA  0.0 12.5 3.7  1.0 0.0 0.0 4.9

所以我们可以剔除它们：

>algae <-algae[-c(62,199),]

在有些问题中，由于大量记录中含有缺失值，用上面的观察方法来检查数据的缺失值是不可行的，我们需要找出缺失值较多的样本所在的行。下面的代码可以帮助我们找出海藻数据集中每行数据的缺失值的个数：

apply(algae,1,function(x) sum(is.na(x)))

apply()函数，它可以把任何其他函数应用到一个多维对象的各个维度上。这个被应用的函数在apply()函数的第三个参数中给出，对数据框的每一行都分别调用该函数。在这里，临时函数的功能是计算对象x中NA的数量。在R中逻辑值TURE等于数值1，逻辑值FALSE等于数值0，这意味着当加一个布尔值向量时，得到向量中TURE的元素的个数。

根据以上代码，可以找出algae中含有给定数目缺失值的行：

>data(algae)
>manyNAs(algae,0.2)

函数manyNAs()的功能是找出缺失值个数大于列数20%的行。函数第二个参数的默认值为0.2。

用下面的代码就无须知道含有缺失值较多的行的具体数量：

>algae <- algae[-manyNAs(algae),]

4.2 用最高频率值来填补缺失值
填补缺失数据最简便和便捷的方法是使用一些代表中心趋势的值。代表中心趋势的值反映了变量分布的最常见值。有多个代表数据中心趋势的指标，例如平均值、中位数、众数等。最适合的选择由变量的分布决定。
对于接近正态的分布来说，所有的观测值都较好地聚集在平均值周围，平均值数就是最佳选择。然而，对于偏态分布，或者有离群值的变量来说，选择平均值就不好。因此，在对变量分布进行检查之前选择平均值作为中心趋势的代表是不明智的。

1. 使用平均值来填补缺失值，代码如下：

>algae[48,'mxPH'] <- mean(algae$mxPH,na.rm=T)

对样本[48]中变量mxPHd的缺失值用平均值填补，因为该变量分布近似正态分布。这里函数mean()计算数值向量的平均值，参数na.rm = T使计算时忽略缺失数据NA.

1. 大多数时候采用一次填补一列中的所有缺失值而不是像上面那样一行一行地逐个填补。以Chla为例，这个变量在第12行上有缺失值。并且Chla的分布偏向于较低的数值，并且它有几个极端值，这些使得平均值不能代表大多数的变量值。因此我们使用中位数来填补这一类的缺失值：

>algae[is.na(algae$Chla),'Chla'] <- median(algae$Chla,na.rm=T)

添加包中提供的函数centralImputation()可以用数据的中心趋势值来填补数据集的所有缺失值。对于数值型变量，该函数用中位数；对于名义变量，它采用众数，代码如下：

>data(algae)
>algae <- algae[-manyNAs(algae),]
>algae <- centralImputation(algae)

第二行代码先去掉数据缺失严重的样本62和199
第三行用centalImputaion()填补缺失值

由于缺失值的存在会导致某些方法不能使用，所有使用上面的方法填补缺失值通常也认为不是很好的方法。虽然上述的简单方法速度快，特别适用于大数据集，但是它可能导致较大的数据偏差，影响后期的数据分析工作。然而，使用无偏方法来寻找最佳数据填补值复杂，对于大型数据挖掘问题可能并不适用。

4.3 用过变量的相关关系来填补缺失值
另一种获取缺失值较少偏差估计值的方法是探寻变量之间的相关关系。如下命令可以得到变量间的相关值：

>cor(algae[,4:18],use="complete.obs")

函数cor()的功能是产生变量之间的相关值矩阵(前3个变量是名义变量，所以计算相关值时不考虑它们)。设定参数use = “complete.obs”时，R在计算相关值时忽略含有NA的记录。相关值在1(或-1)周围表示相应的两个变量之间有强正(或负)线性相关关系。然后利用其他R函数可以得到变量间线性相关的近似函数形式，它可以让我们通过一个已知变量的值计算出另一个未知变量的值。

            mxPH        mnO2          Cl         NO3         NH4         oPO4         PO4        Chla          a1
mxPH  1.00000000 -0.10269374  0.14709539 -0.17213024 -0.15429757  0.090229085  0.10132957  0.43182377 -0.16262986

函数cor()的输出结果并不是很清晰，但可以通过symnum()来改善结果的输出形式。

>symnum(cor(algae[,4:18],use="complete.obs"))

我们发现：变量NH4和NO3之间，变量PO4和oPO4之间的相关性比较强。

开始查找变量之间的相关性之前，我们要剔除样本62和样本199，因为它们有太多变量含有缺失值。样本中的变量NH4和NO3就没有缺失值了。至于变量PO4和oPO4,它们之间的相关性可以帮助填补这两个变量的缺失值。

我们需要找到这两个变量之间的线性相关关系，代码如下：

>data(algae)
>algae <- algae[-manyNAs(algae),]
>lm(PO4 ~ oPO4,data=algae)

Call:
lm(formula = PO4 ~ oPO4, data = algae)

Coefficients:
(Intercept)         oPO4  
     42.897        1.293  

函数lm()可以用来获取形如 Y=β0+β1x1+...+βnxn 的线性模型。如果这两个变量不是同时有缺失值，那么可以通过这个公式计算这些变量的缺失值。线性模型是： PO4=42.897+1.293∗oPO4 。

样本28在变量PO4上有缺失值，可以使用上面的线性关系计算缺失值：

algae[28,'PO4'] <- 42.897 + 1.293 * algae[28,'oPO4']

假设变量有多个缺失值时，我们可以通过构造函数来解决问题：

>data(algae)
>algae <- algae[-manyNAs(algae),]
>fillPO4 <- function(oP) {
   if (is.na(oP)) return(NA)
   else return(42.897 + 1.293 * oP)
}
>algae[is.na(algae$PO4),'PO4'] <- 
    sapply(algae[is.na(algae$PO4),'oPO4'],fillPO4)

fillPO4()函数有一个参数oP来接收变量oPO4的值。函数sapply()的第一个参数是一个向量，第二个参数是一个函数。结果是另一个向量，该向量和第一个参数有相同的长度，元素为第二个参数中的函数应用到第一个参数中向量的每一个元素后得到的结果。

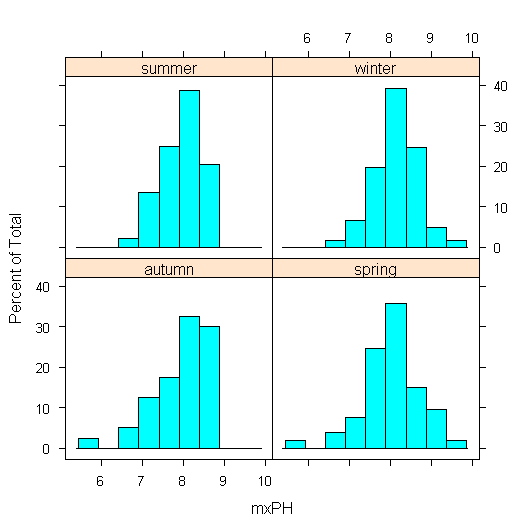
我们还可以试着探索案例数据中含有缺失值的变量和名义变量之间的关系。通过绘制条件直方图来进行：

histogram(~ mxPH | season,data=algae)

我们可以看到上图的季节顺序不是按照自然的时间顺序来的，可以转变数据框中因子季节标签的顺序，这样可以使图形中的季节值为自然时间顺序。代码如下：

>algae$season <- factor(algae$season,levels=c('spring','summer','autumn','winter'))

默认情况下，当把名义变量的值转变为因子时，参数levels假定因子的水平值按照字母字母顺序排列。在本例中，需要因子水平的不同顺序，即季节的时间顺序，所以在因子函数中需要指定因子水平的排序方式。

4.4 通过案列之间的相似性来填补缺失值
不同于探索变量(数据集列)之间的相关性，本节尝试使用案列(数据集行)之间的相似性来填补缺失值。首先我们定义相似性概念。有许多度量相似性的指标，常用的是欧式距离。这个距离可以非正式地定义为任何两个案列的观测值之差的平方和。计算公式如下：

d(x,y)=∑i=0n(xi−yi)2−−−−−−−−−−√

我们考虑两种方法。第一种方法简单地计算这10个最相近的案例的中位数并用这个中位数来填补缺失值。如果缺失值是名义变量，我们采用这10个最相似数据中出现次数最多的值。
第二种方法采用这些最相似数据的加权均值。权重的大小随着距待填补缺失值的个案的距离增大而减少。这里用高斯核函数从距离获得权重。如果相邻个案距待填补缺失值的个案的距离为d，则它的值在加权平均中的权重为： w(d)=e−d 上面的方法可通过函数knnImputation()来实现。

这个函数用一个欧式距离的变种来找到距任何个案最近的k个邻居。这个变种的欧式距离可以应用于同时含有名义变量和数值变量的数据集中。公式如下：

d(x,y)=∑i=1pδi(xi−yi)−−−−−−−−−−−⎷

，其中 δi() 是变量i的两个值之间的距离，即： δi(v1,v2) =

⎧⎩⎨ 1,0,(v1−v2)2,当i是名义变量且v1≠v2时当i是名义变量且v1=v2时当i是数值变量时

使用knnIuputation()函数：

>algae <- knnImputation(algae,k=10)

如果用中位数来填补缺失值，可以使用如下代码：

>algae <- knnImputation(algae,k=10，meth="median")

通过这些简单的操作，数据集中不再含有NA值。为使用R的其他函数进行分析做好充分的准备工作。

5. 获取预测模型
本案例的主要研究目的是预测140个水样中7种海藻的出现频率。假设海藻频率是数值型数据，因此可以考虑进行回归分析(由于我们要预测每种水样的7种频率值，所以我们把这个问题分成7种不同的线性回归)。

简单地说，预测任务是建立一个模型来找到一个数值变量和一组解释变量的关系。预测海藻的两种不同模型：多元线性回归模型和回归树模型。这两个模型以不同的方法处理缺失值问题。R中的线性回归不能使用有缺失值的数据集，而回归树模型可以很自然地处理这些带有缺失值的数据。

5.1 多元线性回归
多元线性回归模型是最常用的统计数据分析方法，该模型给出了一个有关目标变量与一组解释变量关系的线性函数。这里应用根据训练集数据个案的相似性方法来填补缺失值。代码如下：

>data(algae)
>algae <- algae[-manyNAs(algae),]
>clean.algae <- knnImputation(algae,k=10)

得到的数据框clean.algae将不含有缺失值。接下来建立一个用于预测海藻频率的线性回归模型：

>lm.a1 <- lm(a1 ~ .,data=clean.algae[,1:12])

函数lm()建立一个线性回归模型，其中的第一个参数给出了模型的函数形式。函数的形式是用数据中的其他所有变量来预测变量a1，第一个参数中的 点“.”代表数据框中的所有除a1外的变量。函数lm()的结果是一个含有线性模型信息的对象。可以通过如下代码来获取更多线性模型的信息：

>summary(lm.a1)

Call:
lm(formula = a1 ~ ., data = clean.algae[, 1:12])

Residuals:
    Min      1Q  Median      3Q     Max 
-37.679 -11.893  -2.567   7.410  62.190 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)   
(Intercept)  42.942055  24.010879   1.788  0.07537 . 
seasonspring  3.726978   4.137741   0.901  0.36892   
seasonsummer  0.747597   4.020711   0.186  0.85270   
seasonwinter  3.692955   3.865391   0.955  0.34065   
sizemedium    3.263728   3.802051   0.858  0.39179   
sizesmall     9.682140   4.179971   2.316  0.02166 * 
speedlow      3.922084   4.706315   0.833  0.40573   
speedmedium   0.246764   3.241874   0.076  0.93941   
mxPH         -3.589118   2.703528  -1.328  0.18598   
mnO2          1.052636   0.705018   1.493  0.13715   
Cl           -0.040172   0.033661  -1.193  0.23426   
NO3          -1.511235   0.551339  -2.741  0.00674 **
NH4           0.001634   0.001003   1.628  0.10516   
oPO4         -0.005435   0.039884  -0.136  0.89177   
PO4          -0.052241   0.030755  -1.699  0.09109 . 
Chla         -0.088022   0.079998  -1.100  0.27265   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 17.65 on 182 degrees of freedom
Multiple R-squared:  0.3731,    Adjusted R-squared:  0.3215 
F-statistic: 7.223 on 15 and 182 DF,  p-value: 2.444e-12

由R输出的模型诊断信息是 R2 (或者多元 R2 或调整 R2 )。 R2 表明模型与数据的吻合程度，即模型所能解释的数据变差的比例。 R2 接近于1就表明模型拟合得越好。

首先用函数anova()来精简线性模型。当将anova()应用到简单线性模型时，这个函数提供一个模型拟合的方差序贯分析。也就是说，随着公式中项数的增加，模型的残差平方和减少。对前面的模型进行方差分析，代码如下：

>anova(lm.a1)

Analysis of Variance Table

Response: a1
           Df Sum Sq Mean Sq F value    Pr(>F)    
season      3     85    28.2  0.0905 0.9651944    
size        2  11401  5700.7 18.3088  5.69e-08 ***
speed       2   3934  1967.2  6.3179 0.0022244 ** 
mxPH        1   1329  1328.8  4.2677 0.0402613 *  
mnO2        1   2287  2286.8  7.3444 0.0073705 ** 
Cl          1   4304  4304.3 13.8239 0.0002671 ***
NO3         1   3418  3418.5 10.9789 0.0011118 ** 
NH4         1    404   403.6  1.2963 0.2563847    
oPO4        1   4788  4788.0 15.3774 0.0001246 ***
PO4         1   1406  1405.6  4.5142 0.0349635 *  
Chla        1    377   377.0  1.2107 0.2726544    
Residuals 182  56668   311.4                      
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

上面的结果表明变量season对减少模型拟合误差的贡献最小。可以将它从模型中剔除：

>lm2.a1 <- update(lm.a1,.~.-season)

函数update()用于对已知的线性模型进行微小调整，从模型lm.a1中移除变量season以得到一个新的模型。

为了简化向后消元过程，R有一个函数来执行上面所有的过程，下面的代码对初始模型(lm.a1)用向后消元方法得到一个新的线性模型：

>final.lm <- step(lm.a1)

Start:  AIC=1152.03
a1 ~ season + size + speed + mxPH + mnO2 + Cl + NO3 + NH4 + oPO4 + 
    PO4 + Chla

         Df Sum of Sq   RSS    AIC
- season  3    447.62 57116 1147.6
- speed   2    269.60 56938 1149.0
- oPO4    1      5.78 56674 1150.0
- Chla    1    376.96 57045 1151.3
- Cl      1    443.46 57112 1151.6
- mxPH    1    548.76 57217 1151.9
                56668 1152.0
- mnO2    1    694.11 57363 1152.4
- NH4     1    825.67 57494 1152.9
- PO4     1    898.42 57567 1153.1
- size    2   1857.16 58526 1154.4
- NO3     1   2339.36 59008 1158.0

Step:  AIC=1147.59
a1 ~ size + speed + mxPH + mnO2 + Cl + NO3 + NH4 + oPO4 + PO4 + 
    Chla

        Df Sum of Sq   RSS    AIC
- speed  2    210.64 57327 1144.3
- oPO4   1      7.70 57124 1145.6
- Chla   1    346.27 57462 1146.8
- Cl     1    404.10 57520 1147.0
- mnO2   1    456.37 57572 1147.2
- mxPH   1    466.95 57583 1147.2
               57116 1147.6
- NH4    1    776.11 57892 1148.3
- PO4    1    860.62 57977 1148.5
- size   2   2175.59 59292 1151.0
- NO3    1   2420.47 59537 1153.8

Step:  AIC=1144.31
a1 ~ size + mxPH + mnO2 + Cl + NO3 + NH4 + oPO4 + PO4 + Chla

       Df Sum of Sq   RSS    AIC
- oPO4  1     16.29 57343 1142.4
- Chla  1    223.29 57550 1143.1
- mnO2  1    413.77 57740 1143.7
- Cl    1    472.70 57799 1143.9
- mxPH  1    483.56 57810 1144.0
              57327 1144.3
- NH4   1    720.19 58047 1144.8
- PO4   1    809.30 58136 1145.1
- size  2   2060.95 59388 1147.3
- NO3   1   2379.75 59706 1150.4

Step:  AIC=1142.37
a1 ~ size + mxPH + mnO2 + Cl + NO3 + NH4 + PO4 + Chla

       Df Sum of Sq   RSS    AIC
- Chla  1     207.7 57551 1141.1
- mnO2  1     402.6 57746 1141.8
- Cl    1     470.7 57814 1142.0
- mxPH  1     519.7 57863 1142.2
              57343 1142.4
- NH4   1     704.4 58047 1142.8
- size  2    2050.3 59393 1145.3
- NO3   1    2370.4 59713 1148.4
- PO4   1    5818.4 63161 1159.5

Step:  AIC=1141.09
a1 ~ size + mxPH + mnO2 + Cl + NO3 + NH4 + PO4

       Df Sum of Sq   RSS    AIC
- mnO2  1     435.3 57986 1140.6
- Cl    1     438.1 57989 1140.6
              57551 1141.1
- NH4   1     746.9 58298 1141.6
- mxPH  1     833.1 58384 1141.9
- size  2    2217.5 59768 1144.6
- NO3   1    2667.1 60218 1148.1
- PO4   1    6309.7 63860 1159.7

Step:  AIC=1140.58
a1 ~ size + mxPH + Cl + NO3 + NH4 + PO4

       Df Sum of Sq   RSS    AIC
- NH4   1     531.0 58517 1140.4
- Cl    1     584.9 58571 1140.6
              57986 1140.6
- mxPH  1     819.1 58805 1141.4
- size  2    2478.2 60464 1144.9
- NO3   1    2251.4 60237 1146.1
- PO4   1    9097.9 67084 1167.4

Step:  AIC=1140.38
a1 ~ size + mxPH + Cl + NO3 + PO4

       Df Sum of Sq   RSS    AIC
              58517 1140.4
- mxPH  1     784.1 59301 1141.0
- Cl    1     835.6 59353 1141.2
- NO3   1    1987.9 60505 1145.0
- size  2    2664.3 61181 1145.2
- PO4   1    8575.8 67093 1165.5

函数step()使用Akaike信息标准进行模型搜索。默认情况下，搜索使用向后消元法，但通过设置参数direction，可以采用其他的方法。

可以通过下面的代码来获得最后模型的信息：

>summary(final.lm)

Call:
lm(formula = a1 ~ size + mxPH + Cl + NO3 + PO4, data = clean.algae[, 
    1:12])

Residuals:
    Min      1Q  Median      3Q     Max 
-28.874 -12.732  -3.741   8.424  62.926 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 57.28555   20.96132   2.733  0.00687 ** 
sizemedium   2.80050    3.40190   0.823  0.41141    
sizesmall   10.40636    3.82243   2.722  0.00708 ** 
mxPH        -3.97076    2.48204  -1.600  0.11130    
Cl          -0.05227    0.03165  -1.651  0.10028    
NO3         -0.89529    0.35148  -2.547  0.01165 *  
PO4         -0.05911    0.01117  -5.291 3.32e-07 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 17.5 on 191 degrees of freedom
Multiple R-squared:  0.3527,    Adjusted R-squared:  0.3324 
F-statistic: 17.35 on 6 and 191 DF,  p-value: 5.554e-16

这个模型所解释的方差比例( R2 )仍然不是很可观，这样表明对海藻案例应用假定的线性模型是不适合的。

5.2 回归树
本节描述了如何通过建立回归树来预测海藻a1出现的频率。由于这类模型能够处理缺失值，所以这里只需要移除62号和199号水样即可。建立回归树模型的代码如下：

>library(rpart)
>data(algae)
>algae <- algae[-manyNAs(algae), ]
>rt.a1 <- rpart(a1 ~ .,data=algae[,1:12])

第一条指令用于加载R中的rpart添加包，该包中有回归树的实现。最后一条指令用于获取回归树。这里的函数应用的参数形式与lm()函数的参数形式相同。函数rpart()的第二个参数给出用于建立回归树的数据集。

对象rt.a1的内容如下：

>rt.a1

n= 198 

node), split, n, deviance, yval
      * denotes terminal node

 1) root 198 90401.290 16.996460  
   2) PO4>=43.818 147 31279.120  8.979592  
     4) Cl>=7.8065 140 21622.830  7.492857  
       8) oPO4>=51.118 84  3441.149  3.846429 *
       9) oPO4< 51.118 56 15389.430 12.962500  
        18) mnO2>=10.05 24  1248.673  6.716667 *
        19) mnO2< 10.05 32 12502.320 17.646870  
          38) NO3>=3.1875 9   257.080  7.866667 *
          39) NO3< 3.1875 23 11047.500 21.473910  
            78) mnO2< 8 13  2919.549 13.807690 *
            79) mnO2>=8 10  6370.704 31.440000 *
     5) Cl< 7.8065 7  3157.769 38.714290 *
   3) PO4< 43.818 51 22442.760 40.103920  
     6) mxPH< 7.87 28 11452.770 33.450000  
      12) mxPH>=7.045 18  5146.169 26.394440 *
      13) mxPH< 7.045 10  3797.645 46.150000 *
     7) mxPH>=7.87 23  8241.110 48.204350  
      14) PO4>=15.177 12  3047.517 38.183330 *
      15) PO4< 15.177 11  2673.945 59.136360 *

树从R标为1的根节点开始读。在该节点中看到一共有198个水样，海藻a1出现的平均频率为16。99，相对平均值的偏差为90401.29。树的叶子节点在R中由星号标记出来。如果我们想建立一个回归树来预测某个水样的频率，只要从根节点开始根据对该水样检验的结果，追踪某个分支，直到叶节点。叶节点目标变量的平均值就是树的预测值。

我们也可以得到回归树的图形表示。可以用函数plot()和函数text()对树对象绘图即可。也可以使用R添加包中提供了的函数prettyTree()。得到如下图所示：

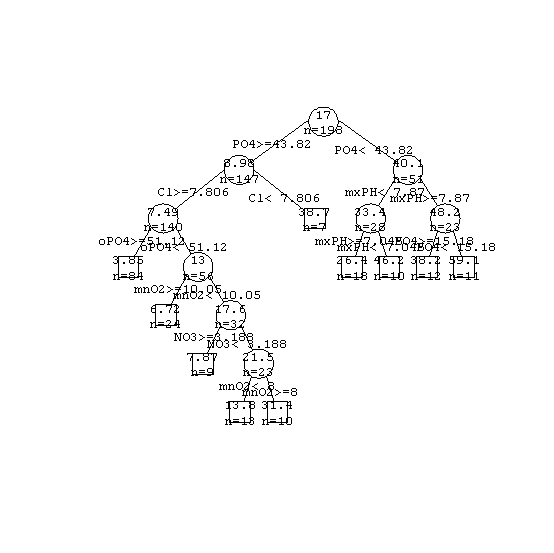
最初生成一颗较大的树，然后通过统计估计删除底部的一些结点来对树进行修剪。这个过程的目的是防止过度拟合。一个过度大的树一般会很好地对训练集数据进行拟合，但是它会拟合给定数据集中的一些虚假的关系，因此当该模型用于新数据的预测时，预测性能很差。所以我们需要一个事后统计估计步骤来避免过度拟合问题(这里没有详细介绍)。

6. 模型的评价和选择
有多种评价模型的标准。其中最流行的标准是计算模型的预测性能，还有其他衡量模型的标准，如模型的可解释性，还有对大型数据挖掘特别重要的标准，即模型的计算效率。

回归模型的预测性能是通过将目标变量的预测值与实际值进行比较得到。一种度量方法是平均绝对误差(MAE)。第一步，获取需要评价模型预测性能的测试集个案的预测值。在R中，要获得任何模型的预测，就要使用函数predict()进行预测。它的第一个参数为需要应用的模型，另一个参数为数据的测试集，输出结果为相应的模型预测值。

>lm.predictions.a1 <- predict(final.lm,clean.algae)
>rt.predictions.a1 <- predict(rt.a1,algae)

得到预测海藻a1的两个模型的预测值。然后可以计算出其平均绝对误差：

>(mae.a1.lm <- mean(abs(lm.predictions.a1-algae[,'a1'])))
>(mae.a1.rt <- mean(abs(rt.predictions.a1-algae[,'a1'])))

另一种流行的误差度量是均方误差(MSE)。代码如下：

>(mse.a1.lm <- mean((lm.predictions.a1-algae[,'a1'])^2))
>(mse.a1.rt <- mean((rt.predictions.a1-algae[,'a1'])^2))

虽然有两种度量方法，问题是如何判断模型的得分是好还是差。能够解决这一问题的误差度量是标准化后的平均绝对误差(NMSE)。这一统计量是计算模型预测性能和基准模型的预测性能之间的比率。通常采用目标变量的平均值来作为基准模型，代码如下：

>(nmse.a1.lm <- mean((lm.predictions.a1-algae[,'a1'])^2)/
                mean((mean(algae[,'a1'])-algae[,'a1'])^2))
>(nmse.a1.rt <- mean((rt.predictions.a1-algae[,'a1'])^2)/
                mean((mean(algae[,'a1'])-algae[,'a1'])^2))

NMSE的取值通常为0-1。如果模型表现优于这个非常简单基准模型预测，那么NMSE应明显小于1。NMSE的值越小，模型的性能就越好。NMSE的值大于1，意味着模型预测还不如简单地把所有个案的平均值作为预测值。

K折交叉验证是获得模型性能可靠估计的一种常用方法，它适用于像本案例这样的小数据集。首先获取K个同样大小的随机训练数据子集。对于这K个子集的每一个子集，用除去它之外的其余K-1个子集建立模型，然后用第K个子集来评估这个模型，最后存储模型的性能指标。对其余的每个子集重复以上的过程，最后有K个性能指标的测量值，这些性能指标是通过在没有用于建模的数据上计算得到的。k折交叉验证估计是这k个性能指标的平均值。

7. 预测7类海藻的频率

（待续…….）