Golang以OO的方式实现二叉查找树
二叉查找树是一种满足如下性质的二叉树:
(1) 某个节点的左子树中的所有节点的值都比这个节点的值小
(2) 某个节点的右子树中的所有节点的值都比这个节点的值大
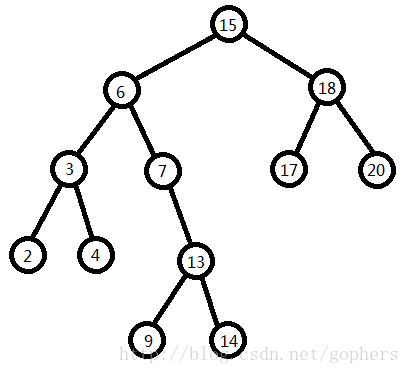
下面有Go实现的非常详尽的代码,采用了Go风格的OO进行了封装。代码中主函数的例子的参照图如下:
这是我的二叉查找树的使用手册:
type BiSearchTree struct
func (bst *BiSearchTree) Add(data float64) //插入节点
func (bst *BiSearchTree) Delete(data float64) //删除节点
func (bst BiSearchTree) GetRoot() *TreeNode //获取根节点
func (bst BiSearchTree) IsEmpty() bool //检查树是否为空
func (bst BiSearchTree) InOrderTravel() //中序遍历(也就是从小到大输出)
func (bst BiSearchTree) Search(data float64) *TreeNode //查找节点
func (bst BiSearchTree) GetDeepth() int //获取树的深度
func (bst BiSearchTree) GetMin() float64 //获取值最小的节点
func (bst BiSearchTree) GetMax() float64 //获取值最大的节点
func (bst BiSearchTree) GetPredecessor(data float64) *TreeNode //获取直接前驱
func (bst BiSearchTree) GetSuccessor(data float64) *TreeNode //获取直接后继
func (bst *BiSearchTree) Clear() //清空树实现代码:
package main
import (
"fmt"
)
type TreeNode struct {
data float64
lchild *TreeNode
rchild *TreeNode
parent *TreeNode
}
type BiSearchTree struct {
root *TreeNode
cur *TreeNode
create *TreeNode
}
func (bst *BiSearchTree) Add(data float64) {
bst.create = new(TreeNode)
bst.create.data = data
if !bst.IsEmpty() {
bst.cur = bst.root
for {
if data < bst.cur.data {
//如果要插入的值比当前节点的值小,则当前节点指向当前节点的左孩子,如果
//左孩子为空,就在这个左孩子上插入新值
if bst.cur.lchild == nil {
bst.cur.lchild = bst.create
bst.create.parent = bst.cur
break
} else {
bst.cur = bst.cur.lchild
}
} else if data > bst.cur.data {
//如果要插入的值比当前节点的值大,则当前节点指向当前节点的右孩子,如果
//右孩子为空,就在这个右孩子上插入新值
if bst.cur.rchild == nil {
bst.cur.rchild = bst.create
bst.create.parent = bst.cur
break
} else {
bst.cur = bst.cur.rchild
}
} else {
//如果要插入的值在树中已经存在,则退出
return
}
}
} else {
bst.root = bst.create
bst.root.parent = nil
}
}
func (bst *BiSearchTree) Delete(data float64) {
var (
deleteNode func(node *TreeNode)
node *TreeNode = bst.Search(data)
)
deleteNode = func(node *TreeNode) {
if node == nil {
return
}
if node.lchild == nil && node.rchild == nil {
//如果要删除的节点没有孩子,直接删掉它就可以(毫无挂念~.~!)
if node == bst.root {
bst.root = nil
} else {
if node.parent.lchild == node {
node.parent.lchild = nil
} else {
node.parent.rchild = nil
}
}
} else if node.lchild != nil && node.rchild == nil {
//如果要删除的节点只有左孩子或右孩子,让这个节点的父节点指向它的指针指向它的
//孩子即可
if node == bst.root {
node.lchild.parent = nil
bst.root = node.lchild
} else {
node.lchild.parent = node.parent
if node.parent.lchild == node {
node.parent.lchild = node.lchild
} else {
node.parent.rchild = node.lchild
}
}
} else if node.lchild == nil && node.rchild != nil {
if node == bst.root {
node.rchild.parent = nil
bst.root = node.rchild
} else {
node.rchild.parent = node.parent
if node.parent.lchild == node {
node.parent.lchild = node.rchild
} else {
node.parent.rchild = node.rchild
}
}
} else {
//如果要删除的节点既有左孩子又有右孩子,就把这个节点的直接后继的值赋给这个节
//点,然后删除直接后继节点即可
successor := bst.GetSuccessor(node.data)
node.data = successor.data
deleteNode(successor)
}
}
deleteNode(node)
}
func (bst BiSearchTree) GetRoot() *TreeNode {
if bst.root != nil {
return bst.root
}
return nil
}
func (bst BiSearchTree) IsEmpty() bool {
if bst.root == nil {
return true
}
return false
}
func (bst BiSearchTree) InOrderTravel() {
var inOrderTravel func(node *TreeNode)
inOrderTravel = func(node *TreeNode) {
if node != nil {
inOrderTravel(node.lchild)
fmt.Printf("%g ", node.data)
inOrderTravel(node.rchild)
}
}
inOrderTravel(bst.root)
}
func (bst BiSearchTree) Search(data float64) *TreeNode {
//和Add操作类似,只要按照比当前节点小就往左孩子上拐,比当前节点大就往右孩子上拐的思路
//一路找下去,知道找到要查找的值返回即可
bst.cur = bst.root
for {
if bst.cur == nil {
return nil
}
if data < bst.cur.data {
bst.cur = bst.cur.lchild
} else if data > bst.cur.data {
bst.cur = bst.cur.rchild
} else {
return bst.cur
}
}
}
func (bst BiSearchTree) GetDeepth() int {
var getDeepth func(node *TreeNode) int
getDeepth = func(node *TreeNode) int {
if node == nil {
return 0
}
if node.lchild == nil && node.rchild == nil {
return 1
}
var (
ldeepth int = getDeepth(node.lchild)
rdeepth int = getDeepth(node.rchild)
)
if ldeepth > rdeepth {
return ldeepth + 1
} else {
return rdeepth + 1
}
}
return getDeepth(bst.root)
}
func (bst BiSearchTree) GetMin() float64 {
//根据二叉查找树的性质,树中最左边的节点就是值最小的节点
if bst.root == nil {
return -1
}
bst.cur = bst.root
for {
if bst.cur.lchild != nil {
bst.cur = bst.cur.lchild
} else {
return bst.cur.data
}
}
}
func (bst BiSearchTree) GetMax() float64 {
//根据二叉查找树的性质,树中最右边的节点就是值最大的节点
if bst.root == nil {
return -1
}
bst.cur = bst.root
for {
if bst.cur.rchild != nil {
bst.cur = bst.cur.rchild
} else {
return bst.cur.data
}
}
}
func (bst BiSearchTree) GetPredecessor(data float64) *TreeNode {
getMax := func(node *TreeNode) *TreeNode {
if node == nil {
return nil
}
for {
if node.rchild != nil {
node = node.rchild
} else {
return node
}
}
}
node := bst.Search(data)
if node != nil {
if node.lchild != nil {
//如果这个节点有左孩子,那么它的直接前驱就是它左子树的最右边的节点,因为比这
//个节点值小的节点都在左子树,而这些节点中值最大的就是这个最右边的节点
return getMax(node.lchild)
} else {
//如果这个节点没有左孩子,那么就沿着它的父节点找,知道某个父节点的父节点的右
//孩子就是这个父节点,那么这个父节点的父节点就是直接前驱
for {
if node == nil || node.parent == nil {
break
}
if node == node.parent.rchild {
return node.parent
}
node = node.parent
}
}
}
return nil
}
func (bst BiSearchTree) GetSuccessor(data float64) *TreeNode {
getMin := func(node *TreeNode) *TreeNode {
if node == nil {
return nil
}
for {
if node.lchild != nil {
node = node.lchild
} else {
return node
}
}
}
//参照寻找直接前驱的函数对比着看
node := bst.Search(data)
if node != nil {
if node.rchild != nil {
return getMin(node.rchild)
} else {
for {
if node == nil || node.parent == nil {
break
}
if node == node.parent.lchild {
return node.parent
}
node = node.parent
}
}
}
return nil
}
func (bst *BiSearchTree) Clear() {
bst.root = nil
bst.cur = nil
bst.create = nil
}
func main() {
var bst BiSearchTree
bst.Add(15)
bst.Add(6)
bst.Add(18)
bst.Add(3)
bst.Add(7)
bst.Add(17)
bst.Add(20)
bst.Add(2)
bst.Add(4)
bst.Add(13)
bst.Add(9)
bst.Add(14)
fmt.Printf("The nodes of the BiSearchTree is: ")
bst.InOrderTravel()
fmt.Printf("\n")
fmt.Printf("The deepth of the tree is: %d\n", bst.GetDeepth())
fmt.Printf("The min is: %g\n", bst.GetMin())
fmt.Printf("The max is: %g\n", bst.GetMax())
if bst.Search(17) != nil {
fmt.Printf("The 17 exists.\n")
}
fmt.Printf("root node's predecessor is: %g\n", bst.GetPredecessor(bst.GetRoot().data).data)
fmt.Printf("root node's successor is: %g\n", bst.GetSuccessor(bst.GetRoot().data).data)
bst.Delete(13)
fmt.Printf("Nodes after delete the 13: ")
bst.InOrderTravel()
fmt.Printf("\n")
}
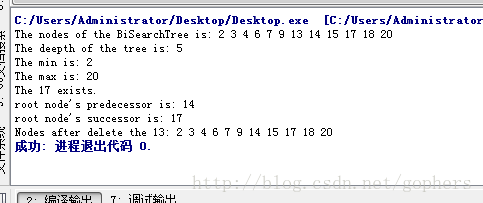
输出结果:
如果转载请注明出处:http://blog.csdn.net/gophers/article/details/23552925