[机器学习] Coursera ML笔记 - 监督学习(Supervised Learning) - Representation
引言
机器学习栏目记录我在学习Machine Learning过程的一些心得笔记,涵盖线性回归、逻辑回归、Softmax回归、神经网络和SVM等等,主要学习资料来自UFLDL Tutorial、Coursera ML和CS231n等在线课程和Tutorial,同时也参考了大量网上的相关资料(在后面列出)。
本文共分为两个部分:
监督学习(Supervised Learning) - Representation
监督学习(Supervised Learning) - Learning
前言
Supervised Learning(监督学习)是指我们来教计算机如何“学习”,其中两个核心问题是:回归 (regression)和分类(classification),都是利用大量的标注数据进行训练,学习得到一个model或者说一个函数,从而对未知数据进行预测。该领域研究的绝大多数课题,都可以归结到这两个问题上。
本文是博主在学习Supervised Learning过程中的一些笔记和心得,重点介绍Supervised Learning领域的基本概念和核心问题,并通过最简单的线性回归和线性分类,介绍监督学习问题的基本求解思路(包括数学描述和求解过程等)。在下一篇博文,会给出相应的代码实现。
文章小节安排如下:
1)有监督学习的概念
2)线性回归
3)线性分类
4)结语
5)参考资料
有监督学习的概念
有监督学习的基本概念,可以参考Andrew Ng老师在讲义中给出的描述:
实验证明大脑利用同一个学习算法实现了听觉、视觉等等所有的功能,这也是神经网络算法美好的愿景。
In supervised learning, we are given a data set and already know what our correct output should look like, having the idea that there is a relationship between the input and the output.
Supervised learning problems are categorized into “regression” and “classification” problems. In a regression problem, we are trying to predict results within a continuous output, meaning that we are trying to map input variables to some continuous function. In a classification problem, we are instead trying to predict results in a discrete output. In other words, we are trying to map input variables into discrete categories.
同时也可以参考wikipedia上的定义:
Supervised learning is the machine learning task of inferring a function from labeled training data.[1] The training data consist of a set of training examples. In supervised learning, each example is a pair consisting of an input object (typically a vector) and a desired output value (also called the supervisory signal). A supervised learning algorithm analyzes the training data and produces an inferred function, which can be used for mapping new examples. An optimal scenario will allow for the algorithm to correctly determine the class labels for unseen instances. This requires the learning algorithm to generalize from the training data to unseen situations in a “reasonable” way.
参考:https://en.wikipedia.org/wiki/Supervised_learning
总结来说,监督学习就是对具有标签(label)的训练样本(train data)进行学习,找到data和label之间的映射关系(mapping,更确切的说是一个function),从而利用该映射关系对无标签的样本进行预测(predict),得到其标签。
在监督学习领域,两大研究分支是:
· Regression(回归)
· Classification(分类)
分类和回归,本质上都是对样本数据的一种预测,区别在于输出变量的类型。
定量输出称为回归,或者说是连续变量预测;
定性输出称为分类,或者说是离散变量预测。
举个例子:
预测明天的气温是多少度,或者预测房价未来的走势,这是一个回归任务;
预测明天是阴、晴还是雨,或者预测房价未来的涨跌,就是一个分类任务。
从数学的角度来说,
分类问题和回归问题都要根据训练样本找到一个实值函数g(x)。
回归问题是:
给定一个新的样本x,根据训练集推断它所对应的输出y(实数)是多少,也就是使用y=g(x)来推断任一输入x所对应的输出值。
分类问题是:
给定一个新的样本x,根据训练集推断它所对应的类别(如:+1,-1),也就是使用y=sign(g(x))来推断任一输入x所对应的类别。
综上,回归问题和分类问题的本质一样,不同仅在于他们的输出的取值范围不同。
分类问题中,输出只允许取两个值;而在回归问题中,输出可取任意实数。分类一般针对离散型结果而言的,回归是针对连续型结果的,本质上是一样的。
补充资料:sign函数(符号函数)
sign(x)或者Sign(x)叫做符号函数,在数学和计算机运算中,其功能是取某个数的符号(正或负):
当x>0,sign(x)=1;
当x=0,sign(x)=0;
当x<0,sign(x)=-1;
补充资料:函数与映射的区别
函数是一种特殊的映射,它要求两个集合中的元素必须是数,而映射中两个集合的元素是任意的数学对象。
在Regression和Classification两个方向再细分下去,又会有无数个值得研究的问题。
在Regression问题上,读者也许接触过回归分析(Regression Analysis)这个概念,也就是一种统计学上分析数据的方法,目的在于了解两个或多个变量间是否相关、相关方向与强度,并对这种相关关系建立数学模型。
机器学习领域的大多数方法来自于统计学,所以这里介绍的Regression问题其实也就是统计学里的Regression Analysis。
回归分析按照涉及的自变量的多少,可分为一元回归分析和多元回归分析;按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。这些问题在Andrew Ng老师的课程上都会有所涉及。
在Classification问题上,名词术语就更多了,也许读者就听过Logistic Regression、Softmax Regression、SVM、决策树(Decision Tree)和神经网络(Neural Network)等等,名字琳琅满目,算法各有不同,但如果深入研究,又会发现这些算法之间似乎又有着紧密的联系。
在学习和应用的过程中,我也是不断经历着迷茫-顿悟-迷茫-顿悟这样的折磨,后面有机会我都会把这些心得体会写出来与大家分享。
另外,关于模式识别和机器学习的关系,我是这样觉得,
Classification问题可以看作是模式识别(Pattern recognition)的核心问题,因此如果梳理模式识别和机器学习的关系,似乎模式识别应该算是机器学习的子领域,如有不对,也请大家指正。
笔者主要的研究方向是图像视频的分析理解,因此在分类算法上接触的也就更多。
Tips:
一些读者会注意到Logistic Regression和Softmax Regression这两个术语都带着Regression,但事实上它们都是分类算法,至于为什么会带Regression这个词,据说是历史原因,等我有空去考证一下再来告诉大家。
对问题的研究一般都是由浅入深,因此下面通过最简单的线性回归和线性分类,来介绍这两种监督学习问题。
线性回归(Linear Regression)
Regression Analysis在需要连续值预测的领域应用十分广泛,比如气温,房价以及股票价格等等。对于笔者这样主要搞图像/视频分析理解的人来说, 回归分析目前用的并不多O(∩_∩)O~,所以这里只做一个粗浅的介绍,同时也引出机器学习领域的一些重要概念,主要参考了Andrew Ng老师的课程以及网上的一些资料。
首先,看一些什么是线性回归:
如果在回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析(Univariate Linear Regression)。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析(Multivariate Linear Regression)。
下面从最简单的一元线性回归入手,逐步了解机器学习中的一些重要概念和方法。
一元线性回归(Univariate Linear Regression)
假设函数(Hypothesis Function)
一元线性回归只有两个变量:自变量x,因变量y
例如面对如下的数据:
x (input) y (output)
0 4
1 7
2 7
3 8
我们希望可以通过这些数据,找到自变量x与因变量y之间的映射函数h(该过程称为拟合(fit)),从而可以对新的x进行预测,得到y。
那么如何找到两个变量之间的映射关系呢?或者说如何对两个变量进行拟合呢?一般来说,我们可以首先对这种映射关系提出一种假设,如下:
![]()
然后利用已知的数据对其中的参数进行求解,再将该函数用于新数据的预测。参数求解的方法有多种,后续会一一提到。
这个线性函数在机器学习领域称为“假设函数(Hypothesis Function)”。参数的求解过程称为“训练(Training) or 学习(Learning)”。
事实上,在机器学习的学习和应用中,我们所要研究和解决的问题,都是提出假设函数,然后求解出其中的参数θ,从简单到复杂的学习型算法,基本都是这个套路。
在一元线性回归中,我们需要求解的就是θ0 and θ1。
代价函数(Cost Function)
求解参数(参数学习)其实就是一个“最优化问题”,因此我们需要定义出目标函数(Objective Function)和优化目标(Optimization Objective)。
在机器学习里,目标函数称为代价函数(Cost Function),用于评判假设函数的优劣,或者说用于评判参数的优劣。
参数优化或者说学习的过程,其实就是朝着某个目标不断调整参数的过程,直到达到某种终结条件。
在回归问题中,常用的代价函数之一是平方误差函数(Squared error function),对于一元线性回归,其定义如下:
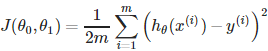
如果将假设函数代入,得到代价函数完整形式:
![]()
其中,
θ0 ,θ1:待拟合的系数
m:样本数量
优化目标(Optimization Objective)
上述代价函数的本质就是计算估计值与实际值的差的累加和,算法的求解目标(优化目标)就是使该代价函数最小化,即:
![]()
这就是算法的优化目标。
算法根据该目标不断调整参数,最终达到某种终结条件,此时得到的参数,被认为是一组较好的可以拟合训练样本数据的参数。
一元线性回归的标准描述
综合上述所提到的假设函数、代价函数和优化目标,我们可以发现一元线性回归问题涉及到4个部分:
假设函数、待优化参数、代价函数、优化目标
其标准化描述如下:
![[机器学习] Coursera ML笔记 - 监督学习(Supervised Learning) - Representation_第1张图片](http://img.e-com-net.com/image/info8/531bd98dde774687b0f3d4b706566382.png)
至此,我们引出了线性回归问题中的几个核心概念。更进一步说,“假设函数、待优化参数、代价函数、优化目标”也就是监督学习问题中的最核心的几个部分,更更进一步说,这也就是机器学习问题中的最核心的几个部分。
无论后面遇到什么机器学习算法,首先要搞清楚的,就是这四个部分。
补充资料:函数与映射的区别
本质是一样的,只是在不同的问题不同的领域里,叫法不一样。例如在这里(机器学习)叫代价函数,也可以叫损失函数;在最优化方法里,叫目标函数。
补充资料:Mean squared error(均方误差,(MSE))
In statistics, the mean squared error (MSE) of an estimator measures the average of the squares of the “errors”, that is, the difference between the estimator and what is estimated.
参考:https://en.wikipedia.org/wiki/Mean_squared_error
多元线性回归(Multivariate Linear Regression)
多元线性回归其实就是回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系。前面我们已经给出了假设函数、代价函数等概念,这里不再赘述,下面直接给出相关定义。
假设函数(Hypothesis Function)
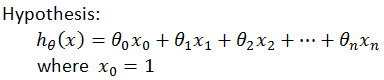
矩阵化定义:
![[机器学习] Coursera ML笔记 - 监督学习(Supervised Learning) - Representation_第2张图片](http://img.e-com-net.com/image/info8/ccbbc4f933d947bba599f951e2e92b4b.jpg)
其中,x0=1
看吧,其实也没什么,无非是变量多了一点而已。在学习Machine Learning过程中,要不断理解模型是什么,例如上面,一个数学函数就是一个机器学习模型。
在回归问题中,包括这里所介绍的线性回归和以后会介绍的非线性回归,hθ(x)就是我们针对回归问题(连续值预测)建立的数学模型,其中θ是我们待求解的模型参数。该模型可以对已知数据进行描述(训练样本),并对未知数据进行预测。
代价函数(Cost Function)
多元线性回归的代价函数形式如下:
![[机器学习] Coursera ML笔记 - 监督学习(Supervised Learning) - Representation_第3张图片](http://img.e-com-net.com/image/info8/36362cc76d8b4e9784becdedd9a45795.png)
线性分类(Linear Classification)
分类问题是监督学习的另一大分支,用于对离散变量预测。例如判断一幅图片是不是狗,或者未来房价是否会涨。
分类算法是Andrew Ng课程中的重要部分,也是我工作学习的重点。分类算法的本质是将一个输入数据映射为一个标签,同样分为两个阶段:
训练,即利用已有的带标签数据,找到数据和标签之间的映射关系(函数);
预测,即利用学习出的函数/模型,对新的数据进行预测,得到其标签。
下面还是从最简单的线性分类器介绍,别看它简单,它可是很多高级算法的基础。同时,也通过线性分类器的介绍,引出分类问题中的一些术语和概念。
那么什么是线性分类器呢?
线性分类器是最简单也很有效的分类器形式,即在样本空间用一个超平面将正负样本分离开,表达式为 y=wx+b。
以二维平面为例,
![[机器学习] Coursera ML笔记 - 监督学习(Supervised Learning) - Representation_第5张图片](http://img.e-com-net.com/image/info8/4c8d82debf3b4e1da95593399c8e9b2b.png)
C1和C2是二维平面的两个类别。可以利用中间的直线将两类样本完全分开,该直线就是一个分类函数。
在线性分类问题中,分类函数是一个线性函数。在一维空间里该函数就是一个点,在二维空间里就是一条直线,三维空间里就是一个平面,可以如此想象下去,如果不关注空间的维数,这种线性函数还有一个统一的名称——超平面(Hyper Plane)!
实际上,线性函数是一个实值函数(即 函数的值是连续的实数),而分类问题需要离散的输出值,例如用 1 表示某个样本属于类别C1,而用 0 表示不属于C1,也就意味着属于C2,这时候只需要在实值函数的基础上附加一个阈值即可,即通过判断分类函数的输出是否大于这个阈值来确定类别归属。
例如有一个线性函数 g(x)=wx+b,我们可以取阈值为0,这样当有一个样本xi 需要判别的时候,就可以通过g(xi) 的值与0比较,确定样本的类别归属。即,若g(xi)>= 0,则判别为类别C1,若g(xi)<0,则判别为类别C2。此时也等价于给函数g(x)附加一个符号函数 sgn(),即f(x)=sgn [g(x)]是我们真正的判别函数。
在已知大量有标签数据的情况下,如果找到这样一个线性函数,就是线性分类器所研究的问题。回想一下在线性回归中的思路,其实这里也是一样的,我们需要针对数据和标签之间的对应关系提出一种假设,并设计一个代价函数用于评判假设函数的优劣,然后利用某种优化方法来求解最优的参数。
下面给出线性分类的假设函数、代价函数和优化目标:
代价函数(Cost Function)
cost of single sample:
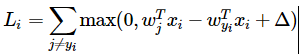
cost of train dataset:
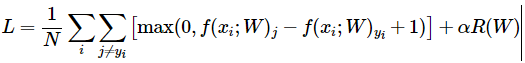
Tips:
如果样本形式如下:
data: (x1, x2), label: 1 or -1
我们构造一个假设函数如下:
f(x)=θ0 + θ1x1 + θ2x2
请问这是几维空间里的函数?
答案:
三维!因为其实这里有一个变量没有写出来,其完整形式应该是:
y=f(x)=θ0 + θ1x1 + θ2x2
Tips:
分类和回归并不是完全独立的两种任务,如果深入思考,会发现分类从某种角度理解,也是一种回归。
关于线性分类器,给大家推荐一份非常好的讲义:
Linear Classifier
http://cs231n.github.io/linear-classify/
Optimization
http://cs231n.github.io/optimization-1/
这是Stanford Fei-Fei Li教授所开设的CS231n的课程讲义,对线性分类器有非常好的介绍,浅显易懂,强烈推荐大家阅读学习。
另外推荐大家阅读一份博客,对线性分类器以及由线性分类器引出SVM的思想有很好的介绍:
SVM入门系列
http://www.blogjava.net/zhenandaci/archive/2015/11/11/212964.html
结语
以上是对有监督学习,以及其中核心的Regression和Classification问题的入门级介绍。其实任何监督学习问题,无论是Regression还是Classification,总结一下都无外乎四个部分:
假设函数、待优化参数、代价函数、优化目标
无论遇到多么复杂的问题,只要把握好这四个部分,就基本都是可以理解的。
本文中,线性分类器并没有展开,因为CS231n讲义中已经写的非常好了,感兴趣的朋友直接学习即可。
下一篇会撰写关于监督式算法的训练/学习方面的内容,并给出实现代码。
本文的文字、公式和图形都是笔者根据所学所看的资料经过思考后认真整理和撰写编制的,如有朋友转载,希望可以注明出处:
[机器学习] Coursera ML笔记 - 监督学习(Supervised Learning) - Representation
http://blog.csdn.net/walilk/article/details/50922854
参考资料
Coursera - Machine learning( Andrew Ng)
https://www.coursera.org/learn/machine-learning
CS231n
http://cs231n.github.io/linear-classify/
http://cs231n.github.io/optimization-1/
SVM入门系列
http://www.blogjava.net/zhenandaci/archive/2015/11/11/212964.html
·
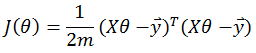
![[机器学习] Coursera ML笔记 - 监督学习(Supervised Learning) - Representation_第4张图片](http://img.e-com-net.com/image/info8/48479b8ba0e04edeb40901da0b2d2bb0.png)