机器学习21：Ensemble

这部分主要介绍Ensemble的方法

为什么我们需要Ensemble的方法

在机器学习的有监督学习算法中，我们的目标是学习出一个稳定的且在各个方面表现都较好的模型，但实际情况往往不这么理想，有时我们只能得到多个有偏好的模型（弱监督模型，在某些方面表现的比较好）。集成学习就是组合这里的多个弱监督模型以期得到一个更好更全面的强监督模型，集成学习潜在的思想是即便某一个弱分类器得到了错误的预测，其他的弱分类器也可以将错误纠正回来。

常见的Ensemble方法

Ensemble一般有下面的bagging、boosting，stacking的方法

Bagging

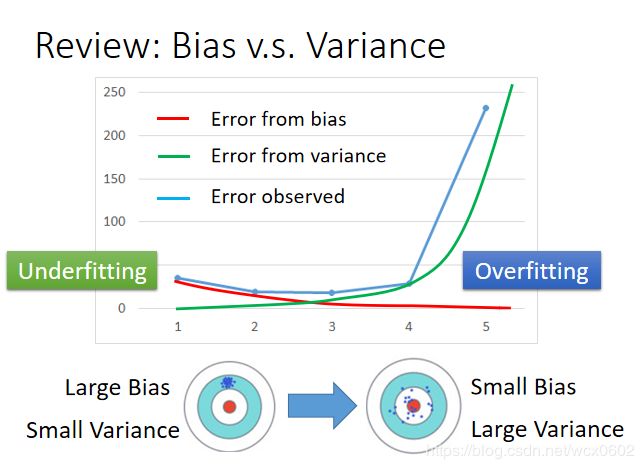
这张图横坐标代表模型的阶次，也可以看做模型的复杂度。红线是模型预测与真实值之间的bias，绿线是模型预测与真实值之间的variance，蓝线是观测误差。我们可以看到随着模型逐渐复杂，训练的结果从underfitting到overfitting。我们使用bagging主要是解决数据充足下的overfiting的问题。

Bagging的原理

使用多组数据，通过训练来得到若干个预测的训练模型，我们可以通过对复杂模型取平均来降低variance。

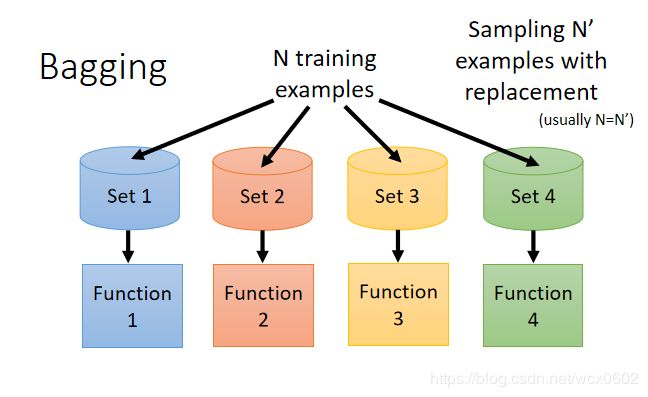
Bagging即套袋法，使用一种有放回的抽样方法，目的为了得到统计量的分布以及置信区间，其算法过程如下：

A）从原始样本集中抽取训练集。每轮从原始样本集中使用Bootstraping的方法抽取n个训练样本（在训练集中，有些样本可能被多次抽取到，而有些样本可能一次都没有被抽中）。共进行k轮抽取，得到k个训练集。（k个训练集之间是相互独立的）

B）每次使用一个训练集得到一个模型，k个训练集共得到k个模型。（注：这里并没有具体的分类算法或回归方法，我们可以根据具体问题采用不同的分类或回归方法，如决策树、感知器等）

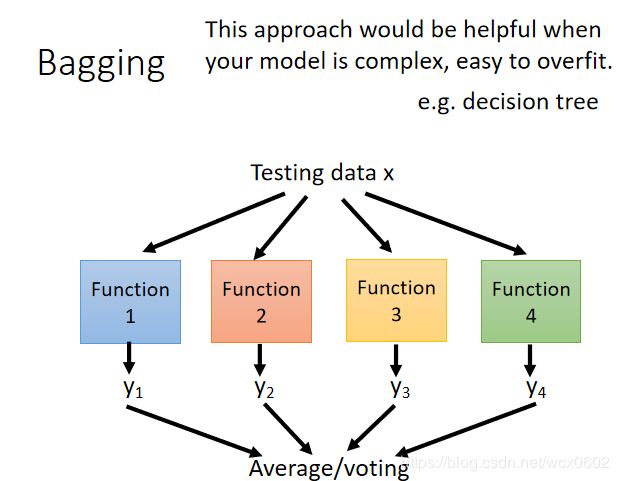C）对分类问题：将上步得到的k个模型采用投票的方式得到分类结果；对回归问题，计算上述模型的均值作为最后的结果。（所有模型的重要性相同

下面介绍一种Bagging的方法

随机森林——random forest，在随机森林中，集成中的每棵树都是由从训练集中抽取的样本（即 bootstrap 样本）构建的。另外，与使用所有特征不同，这里随机选择特征子集，从而进一步达到对树的随机化目的。

因此，随机森林产生的偏差略有增加，但是由于对相关性较小的树计算平均值，估计方差减小了，导致模型的整体效果更好。

下图是一个例子：

我们给出一张图，这张图的人物处的像素值设置为类别1，其余为类别0
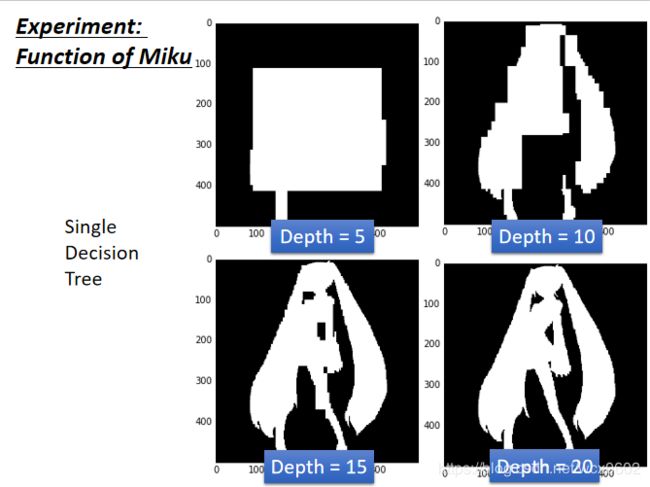我们使用一棵决策树做决策的结果如上图所示，当深度越深效果越好，能够完好的表现出结果，需要大概深度为20.

上面是我们使用Random forest: Bagging of decision tree的方法对数据进行训练。但是仅仅只是随机采样训练数据是不够的。因为相似的数据可能会导致训练出的决策树很相似，从而影响结果。我们需要在每次决策树产生分支时，随机规定了在分支中可使用的分类特征，例如在这一层只能使用横坐标进行分类，或者下一层仅对纵坐标的范围进行分类。

最后使用Out-of-bag的方法进行测试，这个也叫oob方法。例如我们使用x1和x2训练f1，x1和x3训练f3，f2和f4没用使用x1，因此我们使用随机森林f2+f4来评估x1中数据的预测结果。

Boosting的方法

上面说完了Bagging的方法，下面介绍一种Boosting的方法。其主要思想是将弱分类器组装成一个强分类器。
对于这个模型，如果你的错误率可以达到0.5以下，那么就可以使用这种Boosting的方法使得错误率降低到0（理想状态下）。

运行框架是：

1、获得第一个分类器
2、重新选择训练数据集，使得分类器失效，错误率为0.5
3、使用新的训练集训练第二个分类器，循环2和3
4、最后将所有的分类器集合在一起

如何获得不同的训练数据集

1、直接对训练集采样，得到一个新的数据集
2、给训练数据不同的权重值，相当于改变数据分布的占比，来得到新的数据集
3、也可以只改变训练模型的损失函数

Idea of Adaboost

boost的方法有很多，这里介绍一种最经典Adaboost的算法。
其训练集的重现选择是上面的第二种方法：
首先给出错误率的计算公式：

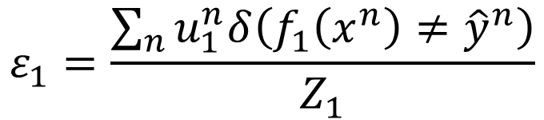
可以简单验证得到上式小于0.5，
改变权重，使得误差到0.5，也就是对于f1，其结果是随机的。之后用这组权重来训练新的模型。

改变权重的方法

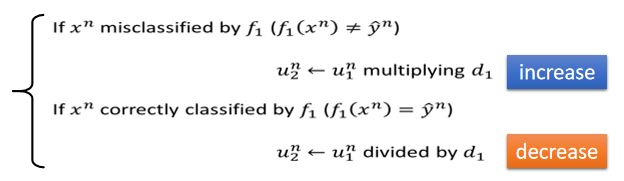
如果x会分类错误，倍乘一个系数d，如果不出错，则会除以系数d
利用错误率0.5，我们可以得到下面的等式

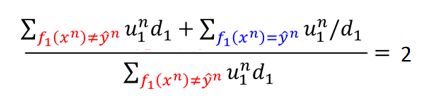
数学推导

对于训练误差有上面的不等式成立

我们先计算Zt是训练数据的权重之和，我们不妨先推导Zt+1的结果。
假设Z的初始值是1，之后每次都是原本的值数乘上一个参数。我们有每个样本的权重递推公式ut，因此我们可以得到Zt+1的表达式，进一步化简合并成后面的形式。

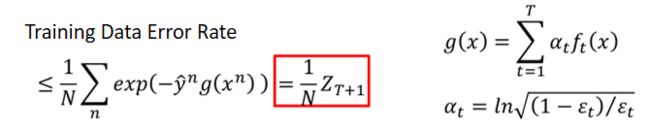
再利用右侧的条件，我们可以写出上面的公式的化简结果，用红框表示的结果

最后我们可以使用Zt的递推公式得到最后的结论，训练误差是无数小于1的值的乘积，随着T增加，逐渐减少

例子

使用Adaboost+Desicion Tree的方法，最后得到的判别结果。

总结通常的Boosting方法

每次寻找一个function f 和一个参数 a 去提高已有的预测模型function g，其输出是function g的结果的符号。

我们的总模型function g的学习目标是是损失函数最小化，也就是下面这个式子

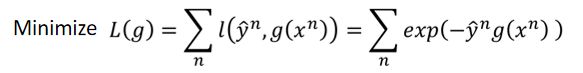
这个式子要求标签 y 和预测值 g 尽可能同号，且乘机结果尽可能大

梯度提升Gradient Boosting

我们从梯度下降的角度看和从boosting的方法来看优化问题

在上面我们得到方向要尽可能一致
这样可以视作最大化下面的式子

极大化的式子前面部分，就是每一个example的adaboost weight

之后是a的值的确定，Gradient Boosting做法是已经确定了f，之后尝试a的值，来找出最好的a。这是因为在前面迭代 f 的过程比较费时间，在这里使用最优的参数a，可以加快整体的收敛时间。使用下面的损失函数，最后找到的结果。

我们可以得到其参数 a 的选择正好的 adaboost 的结果

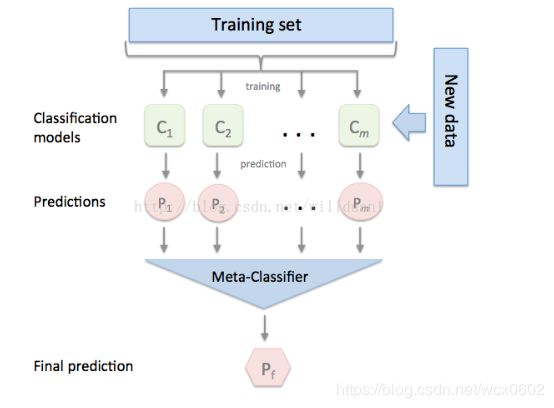
Stacking

这是用来将不同的model的训练结果结合在一起的方法。
Stacking方法是指训练一个模型用于组合其他各个模型。
首先我们先训练多个不同的模型，然后把之前训练的各个模型的输出为输入来训练一个模型，以得到一个最终的输出。
理论上，Stacking可以表示上面提到的两种Ensemble方法，只要我们采用合适的模型组合策略即可。但在实际中，我们通常使用logistic回归作为组合策略。