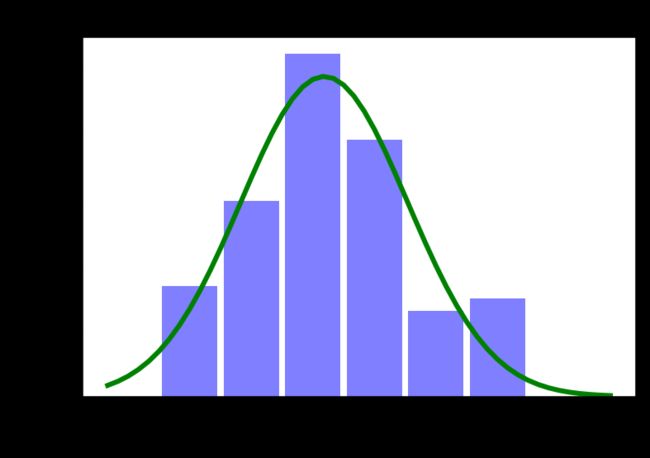
利用python制作正态分布图
1.制作IQ数据图
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt #使用%matplotlib命令可以将matplotlib的图表直接嵌入到Notebook之中,或者使用指定的界面库显示图表,它有一个参数指定matplotlib图表的显示方式
*#inline表示将图表嵌入到Notebook中。
%matplotlib inline
#为了使画出来的图支持 retina格式
%config InlineBackend.figure_format = 'retina'iq_data = pd.read_csv('IQscore.csv')len(iq_data)70
iq = iq_data['IQ']mean = iq.mean()mean100.82857142857142
std = iq.std()
std15.015905990389498
#normfun正态分布函数,mu: 均值,sigma:标准差,pdf:概率密度函数,np.exp():概率密度函数公式
def normfun(x,mu, sigma):
pdf = np.exp(-((x - mu)**2) / (2* sigma**2)) / (sigma * np.sqrt(2*np.pi))
return pdf# x的范围为60-150,以1为单位,需x根据范围调试
x = np.arange(60, 150,1)
# x数对应的概率密度
y = normfun(x, mean, std)
# 参数,颜色,线宽
plt.plot(x,y, color='g',linewidth = 3)
#数据,数组,颜色,颜色深浅,组宽,显示频率
plt.hist(iq, bins =7, color = 'r',alpha=0.5,rwidth= 0.9, normed=True)
plt.title('IQ distribution')
plt.xlabel('IQ score')
plt.ylabel('Probability')
plt.show()2. 制作赛马数据图
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt%matplotlib inline
%config InlineBackend.figure_format = 'retina'stakes_data = pd.read_csv('stakes.csv')len(stakes_data)89
stakes = stakes_data['time']mean = stakes.mean()
mean149.22101123595513
std = stakes.std()std1.6278164717748154
def normfun(x,mu, sigma):
pdf = np.exp(-((x - mu)**2) / (2* sigma**2)) / (sigma * np.sqrt(2*np.pi))
return pdfstakes.max()153.19999999999999
stakes.min()146.0
x = np.arange(145, 155,0.2)
y = normfun(x, mean, std)
plt.plot(x,y,'g',linewidth = 3)
plt.hist(stakes, bins = 6,color = 'b',alpha=0.5, rwidth= 0.9, normed=True)
plt.title('stakes distribution')
plt.xlabel('stakes time')
plt.ylabel('Probability')
plt.show()结论:
1.概率密度函数是图形中的一条线,而概率则是这条线下方一定数值内的面积。
2.求某一个精确数值的概率为0.因为对应的面积趋近于0
3.直方图与正态分布图不完全对应,只有当n充分大,才能更接近于正态分布。
参考资料:
1.使用ipython %matplotlib inline
2.python中求分布函数相关的包
3.python 数学绘图工具 matplotlib 的优化配置
4.【python】matplotlib.pyplot介绍
5.正态分布