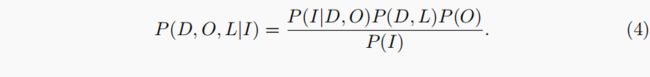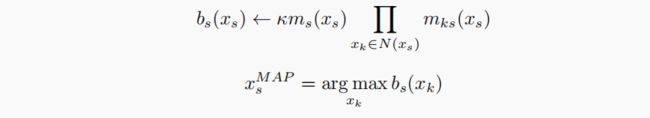Stereo Matching Using Belief Propagation 论文翻译 使用信念传播的立体匹配

Stereo Matching Using Belief Propagation
使用信念传播的立体匹配 （一些数学符号不标准，需要对照原论文阅读）

摘要：本文将立体匹配问题表述为由三个耦合马尔可夫随机场（MRF）组成的马尔可夫网络。这三个MRF模型分别是深度或视差的平滑场、深度不连续的线过程和遮挡的二元过程。在通过引入两个鲁棒函数来消除线过程和二元过程后，应用贝叶斯信念传播（BP）算法得到马尔可夫网络的最大后验概率（MAP）估计。此外，我们扩展了我们的基本立体模型，将未在三个MRF中建模的其他视觉线索（如图像分割）合并，并再次获得最大后验概率解。实验结果表明，在大多数测试用例中，我们的方法都优于最新的立体算法。

1 引言

立体视觉从具有不同视点的两个图像推断场景几何。经典的密集双帧立体匹配从一对已知相机配置下的图像计算密集视差或深度图。一般来说，场景是假设朗伯或不同的角度亮度一致，没有镜面，反射或透明。

由于以下原因，立体匹配很困难。

–噪声：在图像形成过程中，始终存在不可避免的光线变化、图像模糊和传感器噪声。

–无纹理区域：来自高纹理区域的信息需要传播到无纹理区域进行立体匹配。

–深度不连续：信息传播应在对象边界停止。

–遮挡：参考视图中被遮挡的像素无法与其他视图匹配。

因此，立体匹配是一个具有内在模糊性的不适定问题。显然，需要一些约束条件才能对场景结构进行良好的“猜测”。已经提出了许多方法来编码各种约束，例如，亮度一致性、局部平滑约束、广义序约束和唯一性约束。研究表明，在贝叶斯立体匹配方法中，这些约束可以很好地建模。
本文在回顾了第二节关于立体匹配，特别是贝叶斯方法的相关工作后，在第三节中提出了一种贝叶斯立体匹配方法，用于在贝叶斯框架中显式地建模不连续、遮挡和视差场。在第四节中，我们使用贝叶斯信念传播来推断立体匹配。然后在第5节中扩展基本立体模型，以集成多个线索，例如区域相似性。第6节中的实验结果表明，我们的模型是有效且高效的。最后，我们在第7节讨论了为什么我们的基于信念传播的立体匹配算法优于最新的立体算法。

2 相关工作

在本节中，我们将回顾相关的立体算法，尤其是那些使用贝叶斯方法的立体算法。我们向读者提及scharstein和szeliski[21]对密集的两帧立体对应算法的详细和更新分类。它也为立体算法的定量评价提供了实验台。

如果有全局目标函数需要优化，该立体算法称为全局方法。否则称为局部方法。基于局部或窗口的立体匹配方法的核心问题是确定每个像素的最佳支持窗口。理想的支持区域应在无纹理区域较大，并应在深度不连续处停止。固定窗口在深度不连续处明显无效。一些改进的基于窗口的方法，如自适应窗口[16]、可移动窗口[5]和紧凑窗口[23]试图避免窗口跨越深度不连续。

贝叶斯方法（例如，[11,1,5,8,15]）是对不连续和遮挡进行建模的全局方法。盖革等人[11]从匹配过程导出遮挡过程和视差场。假设存在“序约束”和“唯一性约束”，匹配过程就成为一个“寻径”问题，即通过动态规划得到全局最优解。Belhumur[1]定义了从简单场景到复杂场景的一组先验。采用简化的视差与遮挡关系，通过动态规划求解扫描线匹配问题。不同于盖革和贝尔休谟，他们强制实施逐段平滑约束，考克斯等人。[8]和Bobick[5]不需要平滑先验。假设相应的特征是正态分布的，且遮挡代价是固定的，cox还提出了一种仅使用遮挡约束和排序约束的动态规划方法。Bobick结合了基本控制点约束，以降低对遮挡代价的敏感性和Cox动态规划的复杂性。这些方法使用动态规划并假设每个扫描线中的遮挡代价相同。忽略扫描线之间的依赖性会导致视差图中的特征“条纹”。

一般情况下，贝叶斯立体匹配可以表示为一个最大后验概率MRF（MAP-MRF）问题。求解MAP-MRF问题有几种方法：模拟退火[12]、平均场退火[10]、梯度非凸算法（GNC）[4]和变分逼近[14]。虽然理论上实现了全局优化，但通过模拟退火找到一个解通常需要很长的时间。平均场退火是模拟退火的一种确定性近似，它试图对退火过程的统计数据进行平均。它以牺牲解决方案质量为代价减少了执行时间。GNC只能应用于一些特殊的能量函数。变分逼近会收敛到局部极小值。图割（GC）[6]是求解能量函数为Potts或广义Potts的MAP-MRF的一种快速有效的算法。

3 基本立体模型

在我们的工作中，为了显式地处理遮挡和深度不连续性，我们用三个耦合的MRF来模拟立体视觉：D是参考视图的平滑视差场，L是位于双格上的空间线过程，并且显式地表示深度不连续性的存在与否，O是一个表示参考视图中遮挡区域的空间二元过程。图1演示了一维情况下的这些过程。通过使用Bayes规则，给定一对立体图像（I=（IL，IR），其中IL是左图像和参考图像），D，L和O上的联合后验概率为：

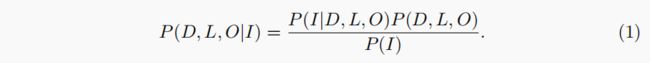
在没有遮挡的情况下，{D，L}是耦合的MRF，它用两个随机场来模拟分段平滑曲面：一个表示估计所需的变量，另一个表示其不连续性。该模型由[12]提出。然而，立体视觉中的遮挡问题并没有明确地包含在这种模型中。在图像形成中，分段平滑场景被投影到一对立体图像上。某些区域仅在一个图像中可见。对于遮挡区域中的每个像素，其他视图中没有匹配的像素。我们假设概率P（I D，O，L）与L无关，因为观测是基于像素的，并且忽略了O与{D，L}之间的统计相关性。

基本立体模型现在变成

3.1 可能性

假设观测噪声遵循独立同分布（i.i.d），我们可以将可能性P（I D，O）定义为：

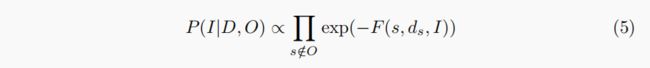
其中F（s，ds，I）是给定观测 I 视差为ds的像素s的匹配代价函数.我们的概率只考虑非遮挡区域的像素，因为遮挡区域像素的概率不能很好地定义。我们使用可证明为对采样不敏感的像素差异性[2]：

其中

s是右视图中视差为ds的s的匹配像素，I-R（s）是s和其左侧相邻像素之间的线性插值亮度，
I+R（s）右侧的，d（s，s，i）是d（s，s，i）的对称版本,σf为要估计的方差。

3.2 先验

直接导出适当的先验来编码约束不仅困难，而且也可能导致过多烦人的超参数而无法容易地找到解决方案
。马尔可夫性质断言场中一个点的概率只取决于它的邻近点。通过指定s点的一阶邻域
g（s）和n（s）={t t>s，t∈g（s）}，先验3可展开为：

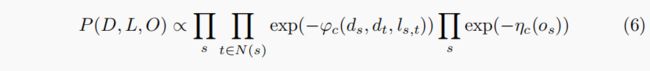
式中，Ψc（ds，dt，ls，t）是ds，dt和ls，t的联合团势函数，ηc（os）是os的团势函数。üc（ds，dt，ls，t）和ηc（os）是用户自定义函数，用于强制立体匹配的约束。_c（ds，dt，ls，t）和ηc（os）也决定了{D，L，O}的分布。为了加强ds和ls之间的空间相互作用，我们定义了_c（ds，ls）如下：

其中（ds，dt）惩罚相邻点s之间不存在间断时的不同分配值，而c（ls，t）惩罚点s和t之间出现间断。
结合（5）、（6）和（7），我们的基本立体模型变成：

4 信念传播的近似推理

在最后一节中，我们用三个耦合的MRF来建模立体匹配。将MRFs转换成相应的马尔可夫网络后，利用近似推理算法循环信念传播来逼近立体匹配的后验概率。

4.1 从线过程到离群过程

在连续MRF和两个二元MRF中，不仅很难指定适当的形式，而且很难进行推理。幸运的是，线过程和鲁棒统计的统一[3]为我们从最大后验概率问题中消除二元随机变量提供了一种方法。如果我们通过忽略遮挡位置的空间相互作用来简化ηc（os）
（ηc（os）的完整形式应为：

其中，η（os）是惩罚遮挡发生的单点团势函数，而η（os，ot）是惩罚os和ot的不同分配值的双点团势函数。）

我们可以将最大后验概率问题改写为：

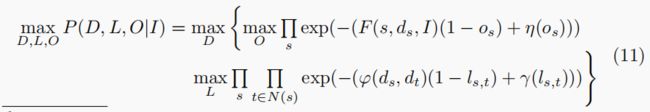
现在，我们将二元过程lst和os升级为模拟进程last和oas（“异常值过程”[3]），通过允许0≤laST≤1且0≤OAS≤1。对于第一项，

其中

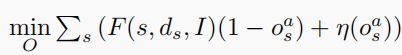
是鲁棒估计量的目标函数。这个鲁棒估计量的鲁棒函数是

对于第二项，我们也有一个鲁棒函数rp（ds，dt）：

我们得到了由两个鲁棒函数定义的D上的后验概率：

因此，我们不仅通过一个异常值过程消除了两个模拟线过程，而且还对测量中的异常值进行了建模。我们将遮挡过程和深度不连续过程的先验模型显式地转换为定义两个鲁棒函数来隐式地建模遮挡和不连续。
本文从总方差（TV）模型[18]出发，利用势函数ρ（x）=x的不连续性，导出了我们的鲁棒函数。我们将此势函数截断为鲁棒函数：

图2显示了我们的鲁棒函数的不同形状。通过改变参数e和σ，我们控制了鲁棒函数的形状，从而控制了后验概率。

4.2 信念传播

与我们的后验概率（15）最相似的模型是s&s的[20]。与使用非线性扩散算法的s&s不同，我们通过信念传播来解决这个最大后验概率问题。信念传播是Pearl[19]在无环信念网络中提出的一种精确推理方法。循环信念传播就是忽略网络中环的存在的信念传播。尽管存在网络环路，但它已成功地应用于一些视觉[9]和通信[24]问题。

在概率图模型的文献中，D上的后验概率（15）正是一个马尔可夫网络，如图3所示。在马尔可夫网络中，立体模型中的随机变量ds由一个隐藏结点xs表示。“私有”观测结点ys连接到每个xs。每个ys是一个向量，其中每个元素是给定结点xs的不同分配的匹配代价。通过表示x={xs}和y={ys}，（15）可以用xs和ys表示：

其中

Ψst（xs，xt）称为结点xs与xt之间的相容矩阵，Ψs（xs，yt）称为结点xs的局部证据。如果视差等级为L，则Ψst（xs，xt）为L×L矩阵和Ψs（xs，ys）是L维向量。

信念传播是一种在网络中传播信息的迭代推理算法。设mst（xs，xt）为结点xs发送给xt的消息，ms（xs，ys）为观察到的结点ys发送给结点xs的消息，bs（xs）为在结点xs的信念。注意mst（xs，xt）、ms（xs，ys）和bs（xs）都是一维向量。我们将MST（xs，xt）简化为MST（xt），将MS（xs，ys）简化为MS（xs）。有两种不同消息更新规则的BP算法：“最大乘积”和“和积”，分别最大化网络的联合后验概率和每个结点的边缘后验概率。标准的“最大积”算法如下所示。

1. 将所有消息初始化为均匀分布
2. 迭代更新 i=1:T的消息
   
3. 计算信念
   
   例如，在图3中，从结点x1发送到x2的新消息被更新为：
   
   结点x1处的信念计算为：
   
   （两条消息的乘积为按分量的乘积）。k是归一化常数。

5 整合多个线索

可以结合更多的约束和先验（例如，边、角、连接、分割、可见性）来改进立体匹配。例如，最近提出了一种基于分割的立体算法[22]，该算法基于在分割区域的边界上出现深度不连续的假设。在[22]中，分割结果被用作硬约束。在我们的工作中，我们使用图像分割，但是在概率框架下，我们将分割结果作为软约束（先验）合并到我们的基本立体模型中。
通过附加线索，我们扩展了基本立体模型（15）：

其中，ρpcue（ds，dt）编码点之间的一些约束。为了整合图像分割中的区域相似性，我们将ρpcue（ds，dt）定义为：

其中seg（s）是点s处的分割结果的标签。λseg越大，在相邻点之间传递消息的难度越大。换句话说，随着λseg的增加，来自邻域的影响变小。在我们的实验中，分割标签是由Mean-Shift算法产生的[7]。在我们实验中使用的所有图像中，执行时间通常只有几秒。
根据（15），相容矩阵Ψst（xs，xt）可以重写为：

图4显示了当xs和xt位于同一区域和不同区域时，Ψst（xs，xt）的第一行。

6 实验结果

在本文中，我们使用[21]中提出的质量度量和基于表1中列出的已知基本真实数据的度量来评估我们的立体算法的性能。尤其是，BO表示立体算法的总体性能。

测试数据集由四对图像组成：“地图”、“筑波”、“锯齿”和“金星”[21]。“筑波”是一个复杂的室内环境，具有倾斜的表面，包含许多整数值的视差。其他对主要由倾斜的平面组成。

表2显示了将我们的bp算法应用于所有四对图像的结果。它还列出了其他立体算法的结果。此表由Scharstein和Szeliski提供（详细信息请参见http://www.middlebury.edu/stereo/results.html）。我们在第一行和第二行分别显示了将图像分割与立体匹配相结合和不结合的结果。

对于像“筑波”这样复杂的环境，结合图像分割可以显著地提高立体匹配效果，BO误差减少40%。事实上，我们的算法是“筑波”的最佳算法，并且优于被广泛认为是最先进的立体匹配算法图割（带遮挡）[17]。我们的算法在其他三个数据集“锯齿”、“维纳斯”和“地图”上与其他立体算法很好地竞争。有趣的是，对于这三个具有简单倾斜曲面的数据集，如从第一行和第二行所看到的那样，合并图像分割并不一定改善立体匹配。

图5和图6显示了我们的算法得到的结果。利用mean-shift算法得到分割图，默认参数由[7]给出。注意，在我们的BP算法中，对所有图像对使用了一组固定的参数{ed=0.05，σd=0.6，ep=0.01，σp=8}。显然，这组参数不是“地图”数据的最佳参数，因为该数据的视差范围几乎是“筑波”数据视差范围的两倍。

我们的BP算法的复杂度是O（L2NT），其中N是像素数，L是视差数，T是迭代次数。对于“筑波”数据，在奔腾III 500兆赫PC上花费了288秒，与[21]中的图形切割算法相当或略好。

实验中还发现了BP算法的局部振荡现象。在固定次数的迭代之后执行时间平均操作：

这种启发式方法在我们的实验中很有效。

7 讨论

为什么BP有效？BP算法的魔力在于它强大的消息传递能力。根据当前迭代发送结点发出的所有信息，消息表示接收结点处于某视差的概率。消息传递有两个重要属性。首先，它是不对称的。高置信度结点到低置信度结点的消息熵小于低置信度结点到高置信度结点的消息熵。其次，它是自适应的。差异较大的一对结点之间的消息影响将进一步减弱。

因此，BP的消息传递为立体匹配提供了一种时变自适应平滑机制，可以自然地处理无纹理区域和深度不连续性。例如，在没有纹理的区域，消息的影响可以传递很远。另一方面，不连续区域的影响会迅速减弱。图7显示了一个例子中的自适应平滑过程。在图7中，从[16]和[20]中使用的图像对修改图像对。基线方向的线性渐变用作基本亮度模式。背景和前景的视差分别为2和5。与[16]或[20]不同的是，在ramp1对的前景中心重叠有一个更小的纯无纹理正方形。

我们使用熵H（b）=-i bilogbi来测量信念的置信度，使用对称形式的kullback-leiber（kl）散度kls（b1 b2）=i（b1i）-b2i）log（b1i b2i）来测量信念b1和b2之间的差异。熵越小，信念的可信度越高。较大的散度代表信念之间的较大差异。如图所示，信念的熵图表示每个结点的视差估计的置信度。显然，每个结点的置信度随着每次迭代而增加。请注意，遮挡区域和角点的置信度低于其他区域。这说明概率方法不仅输出一个解，而且输出它的确定性。信念的散度图显示了消息传递的停止位置。收敛后的散度图说明了理想的支持区域。

假设和未来的工作。

与能量最小化技术相比，贝叶斯方法具有所有假设都需要明确作出的优势。事实上，为了应用BP，我们在模型中做了三个重要的假设（2,3,10）。虽然我们的模型得到了很好的实验结果，但是当这些假设被打破时的情况值得研究。还可以寻求许多其他未来的方向。自然地，我们计划将我们的工作扩展到多基线立体。我们也在研究如何改进立体匹配与其他基于马尔可夫网络的贝叶斯推理技术，如广义BP。