线性回归模型-岭回归Ridge Regression

1. 岭回归Ridge Regression

岭回归用于解决最小二乘法存在的一些问题, 通过引入一个对参数大小的惩罚项, 减小参数值(接近0). 岭回归的最佳参数是使残差的平方和最小.
$\underset{w}{\min }{\Vert Xw-y\Vert }_2^2+\alpha {\Vert w\Vert }_2^2$
这里的$\alpha$是一个控制参数收缩量的参数, $\alpha$的值越大, 参数收缩的幅度越大, 那么参数就越平滑, 共线性表现越鲁棒.
与其他线性模型一样, 岭回归也要通过fit方法输入X和y来进行训练, 训练好的参数w存在coef_中.

2. 岭回归参数正则化的效果

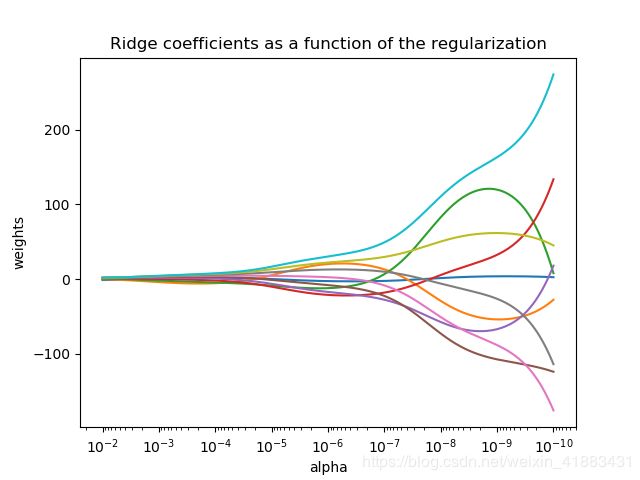
下图中用岭回归作为estimator,每个不同的颜色代表参数向量中的不同的特征, 并且作为一个正则化参数$\alpha$的函数展示出来.
这个例子也说明了应用岭回归处理高度的敏感的矩阵, 有一些矩阵, 轻微的改变目标变量能引起参数的剧烈变化, 这种情况下, 设定一个合理的$\alpha$值来减少这种变化往往是非常有用的.
当$\alpha$非常大的时候, 正则效果主导了方差损失, 并且参数会十分接近0.当$\alpha$趋近于0时, 参数的值会趋近于最小二乘法的参数, 参数的变化幅度很大. 实际应用过程中, 平衡这两个方面的影响找到一个理想的alpha是很重要的.

2.1 代码

  1 print(__doc__)
  2 
  3 import numpy as np
  4 import matplotlib.pyplot as plt
  5 from sklearn import linear_model
  6 
  7 # X is the 10*10 Hilbert matrix
  8 X = 1. / (np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis])
  9 y = np.ones(10)
 10 # print(np.arange(1, 11))
 11 # print('+++++++++++++++++++++')
 12 # print(np.arange(0, 10))
 13 # print('+++++++++++++++++++++')
 14 # print(np.arange(0, 10)[:, np.newaxis])
 15 # print('+++++++++++++++++++++')
 16 # print(np.arange(1, 11) + np.arange(0, 10))
 17 # print('+++++++++++++++++++++')
 18 # print(np.arange(1, 11) + np.arange(0, 10)[:, np.newaxis])
 19 # print('+++++++++++++++++++++')
 20 # print(X)
 21 # print('+++++++++++++++++++++')
 22 
 23 # compute paths
 24 n_alphas = 200
 25 alphas = np.logspace(-10, -2, n_alphas)
 26 
 27 coefs = []
 28 for a in alphas:
 29     ridge = linear_model.Ridge(alpha = a, fit_intercept = False)
 30     ridge.fit(X, y)
 31     coefs.append(ridge.coef_)
 32 # print(coefs)
 33 
 34 # Display results
 35 ax = plt.gca()
 36 
 37 ax.plot(alphas, coefs)
 38 ax.set_xscale('log')
 39 ax.set_xlim(ax.get_xlim()[::-1]) # reverse axis
 40 plt.xlabel('alpha')
 41 plt.ylabel('weights')
 42 plt.title('Ridge coefficients as a function of the regularization')
 43 plt.axis('tight')
 44 plt.show()

运行结果

3. 设置正则参数:广义交叉验证

可以使用sklearn内置的RidgeCV方法来设置岭回归$\alpha$参数. 该方法的工作方式与GridSearchCV相同，只是它默认为广义交叉验证Generalized Cross-Validation（GCV）, 是一种高效的leave-one-out交叉验证.

3.1 示例

3.1.1 代码

  1 from sklearn import linear_model
  2 
  3 reg = linear_model.RidgeCV(alphas = [0.1, 1.0, 10.0], cv = 3)
  4 reg.fit([[0, 0], [0, 0], [1, 1]], [0, 0.1, 1])
  5 # RidgeCV(alphas=[0.1, 1.0, 10.0], cv=3, fit_intercept=True, scoring=None, normalize=False)
  6 print(reg.alpha_)

Reference

• numpy.logspace用法
• sklearn官方文档