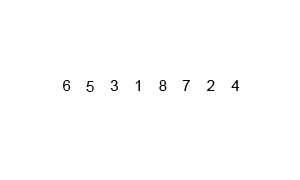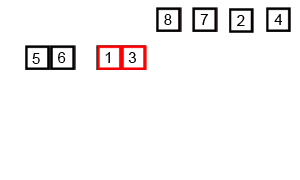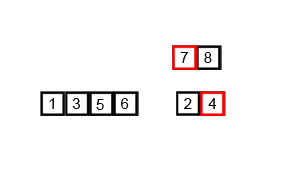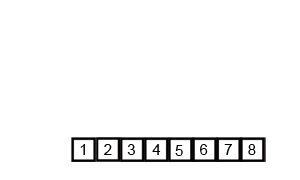【算法导论1】插入排序和归并排序

插入排序

设想有一数组：int [] a = {1,3,4,6,2}
那么插入排序，就是每次取出一个元素，把他重新插入到正确的位置
a = {1,3,4,6,2}
a = {1,3,4,6,2}
a = {1,3,4,6,2}
a = {1,2,3,4,6}
但是，会发现，这样运行的效率并不高。

此处，引入一个数学符号θ：
比如：2n³-5n²+2n+1，去除低阶项，去除常系数，就是θ。此处2n³-5n²+2n+1=θ(n³)
θ(n³)能描述一个函数式的图形走势，因为当n越大，对于图形影响最大的，就是n³项。

同理，在插入排序中，可以用 T(n) 来表示用时的预期值，时间复杂度。
此时，T(n) = ∑θ(n)，其中n∈(1,n)，其实就是一个算术级数（1+2+3+···+n）=((1+n)n)/2=θ(n²)；那么T(n)=θ(n²)。
所以，插入排序的时间复杂度为θ(n²)。

归并排序

设一数组为A[n]，那么首先将其分成两份，分别为A[1~n/2]和A[(n/2)+1~n]。然后对两个子数组进行排序。
比如：
子数组11,3,5,11
子数组22,4,8,9

• 1和2相比，1较小，1被拿到新的数组中→tmp={1}
• 3和2相比，2较小，2被拿到新的数组中→tmp={1,2}
• 如此循环，总共需要n次对比才能排序完成，所以此次排序的时间复杂度为θ(n)

那么，T(n) = 2T(n/2) + θ(n)，此时，可以引入递归树的概念解决。
像这种公式，第一个2说明是二叉树，一分为2；第二个n/2，说明他的儿子们所占用的数据只有一半，也就是说：
T（n/2）=2T（n/4）+cn/2；


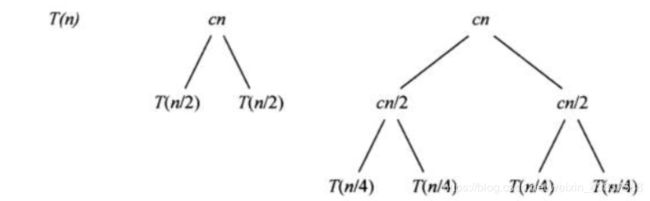
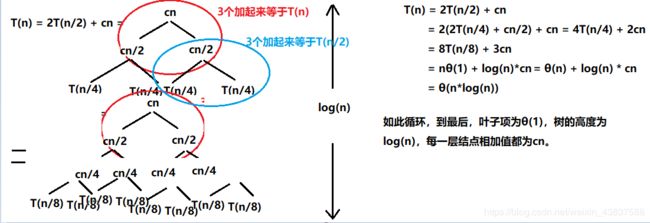
所以，归并排序的时间复杂度为θ(n*log(n))，那么归并排序在n越大的情况下，速度就比插入排序快。

代码段

1. 插入排序

public static int[] InsertionSort(int[] input){
        int tmp = 0;
        int j;
        for (int i = 1; i < input.length; i++){
            tmp = input[i];
            //  1 3 4 2这种，利用j>0 且 tmp 0 && tmp < input[j-1]; j--){
                input[j] = input[j-1];
            }
            input[j] = tmp;// 把2插入到腾出的空间
        }
        return input;
    }

2. 归并排序
   

    public static void mergeSort(int[] input, int start, int end) {
        if (start < end) { // 当子序列剩下一个元素时，结束递归拆分
            int mid = (start + end) / 2;
//            System.out.print(mid+","); // 输出3,1,0,2,5,4前面310是递归拆左边的数组，254是右边的
            mergeSort(input, start, mid);
            mergeSort(input, mid + 1, end);
            merge(input, start, mid, end); // 合并
            System.out.println(start+","+mid+","+end);
        }
    }

    private static void merge(int[] input, int left, int mid, int right) {
        int[] tmp = new int[a.length];//辅助数组
        int p1 = left, p2 = mid + 1, k = left;//p1、p2是检测指针，k是存放指针
        while (p1 <= mid && p2 <= right) {
            if (a[p1] <= a[p2])
                tmp[k++] = a[p1++];
            else
                tmp[k++] = a[p2++];
        }

        while (p1 <= mid) tmp[k++] = a[p1++];//如果第一个序列未检测完，直接将后面所有元素加到合并的序列中
        while (p2 <= right) tmp[k++] = a[p2++];//同上

        //复制回原素组
        for (int i = left; i <= right; i++)
            a[i] = tmp[i];

    }