十大经典排序算法——归并排序 (Java、JavaScript、PHP、Python、Go语言实现
十大经典排序算法之——归并排序
本文主要介绍十大经典排序算法中的“归并排序”,并附上归并排序算法的Java、JavaScript、PHP、Python、Go语言实现。
1、十大经典排序算法介绍
排序算法可以分为内部排序和外部排序,内部排序是数据记录在内存中进行排序,而外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。常见的内部排序算法有:插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。
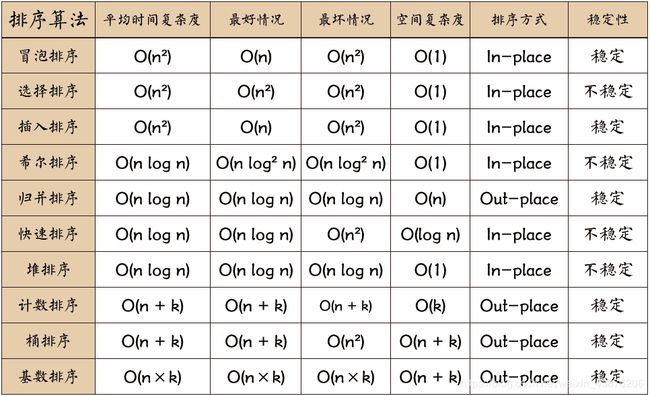
2、十大经典排序算法比较
注:关于时间复杂度
1.平方阶 (O(n2)) 排序 各类简单排序:直接插入、直接选择和冒泡排序。
2.线性对数阶 (O(nlog2n)) 排序 快速排序、堆排序和归并排序。
3.O(n1+§)) 排序,§ 是介于 0 和 1 之间的常数。希尔排序。
4.线性阶 (O(n)) 排序 基数排序,此外还有桶、箱排序。
注:关于稳定性
稳定性:排序后 2 个相等键值的顺序和排序之前它们的顺序相同
稳定的排序算法:冒泡排序、插入排序、归并排序和基数排序。
不是稳定的排序算法:选择排序、快速排序、希尔排序、堆排序。
相关名词解释:n:数据规模,k:“桶”的个数,In-place:占用常数内存,不占用额外内存,Out-place:占用额外内存。
3、细说归并排序
3.1 归并排序介绍
归并排序(Merge sort)是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
作为一种典型的分而治之思想的算法应用,归并排序的实现由两种方法:
•自上而下的递归(所有递归的方法都可以用迭代重写,所以就有了第 2 种方法);
•自下而上的迭代;
和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是 O(nlogn) 的时间复杂度。代价是需要额外的内存空间。
3.2 归并排序算法步骤
1.申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
2.设定两个指针,最初位置分别为两个已经排序序列的起始位置;
3.比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
4.重复步骤 3 直到某一指针达到序列尾;
5.将另一序列剩下的所有元素直接复制到合并序列尾。
3.3 归并排序动画演示
从这张动图我们可以清晰、形象得看出“归并排序”的“归并”意义所在,可以看出在归并排序中指针的作用。
3.4 归并排序算法的代码实现
3.4.1 Java实现
public class MergeSort implements IArraySort {
@Override
public int[] sort(int[] sourceArray) throws Exception {
// 对 arr 进行拷贝,不改变参数内容
int[] arr = Arrays.copyOf(sourceArray, sourceArray.length);
if (arr.length < 2) {
return arr;
}
int middle = (int) Math.floor(arr.length / 2);
int[] left = Arrays.copyOfRange(arr, 0, middle);
int[] right = Arrays.copyOfRange(arr, middle, arr.length);
return merge(sort(left), sort(right));
}
protected int[] merge(int[] left, int[] right) {
int[] result = new int[left.length + right.length];
int i = 0;
while (left.length > 0 && right.length > 0) {
if (left[0] <= right[0]) {
result[i++] = left[0];
left = Arrays.copyOfRange(left, 1, left.length);
} else {
result[i++] = right[0];
right = Arrays.copyOfRange(right, 1, right.length);
}
}
while (left.length > 0) {
result[i++] = left[0];
left = Arrays.copyOfRange(left, 1, left.length);
}
while (right.length > 0) {
result[i++] = right[0];
right = Arrays.copyOfRange(right, 1, right.length);
}
return result;
}
}
3.4.2 JavaScript实现
function mergeSort(arr) { // 采用自上而下的递归方法
var len = arr.length;
if(len < 2) {
return arr;
}
var middle = Math.floor(len / 2),
left = arr.slice(0, middle),
right = arr.slice(middle);
return merge(mergeSort(left), mergeSort(right));
}
function merge(left, right)
{
var result = [];
while (left.length && right.length) {
if (left[0] <= right[0]) {
result.push(left.shift());
} else {
result.push(right.shift());
}
}
while (left.length)
result.push(left.shift());
while (right.length)
result.push(right.shift());
return result;
}
3.4.3 PHP实现
function mergeSort($arr)
{
$len = count($arr);
if ($len < 2) {
return $arr;
}
$middle = floor($len / 2);
$left = array_slice($arr, 0, $middle);
$right = array_slice($arr, $middle);
return merge(mergeSort($left), mergeSort($right));
}
function merge($left, $right)
{
$result = [];
while (count($left) > 0 && count($right) > 0) {
if ($left[0] <= $right[0]) {
$result[] = array_shift($left);
} else {
$result[] = array_shift($right);
}
}
while (count($left))
$result[] = array_shift($left);
while (count($right))
$result[] = array_shift($right);
return $result;
}
3.4.4 Python实现
def mergeSort(arr):
import math
if(len(arr)<2):
return arr
middle = math.floor(len(arr)/2)
left, right = arr[0:middle], arr[middle:]
return merge(mergeSort(left), mergeSort(right))
def merge(left,right):
result = []
while left and right:
if left[0] <= right[0]:
result.append(left.pop(0));
else:
result.append(right.pop(0));
while left:
result.append(left.pop(0));
while right:
result.append(right.pop(0));
return result
3.4.5 Go语言实现
func mergeSort(arr []int) []int {
length := len(arr)
if length < 2 {
return arr
}
middle := length / 2
left := arr[0:middle]
right := arr[middle:]
return merge(mergeSort(left), mergeSort(right))
}
func merge(left []int, right []int) []int {
var result []int
for len(left) != 0 && len(right) != 0 {
if left[0] <= right[0] {
result = append(result, left[0])
left = left[1:]
} else {
result = append(result, right[0])
right = right[1:]
}
}
for len(left) != 0 {
result = append(result, left[0])
left = left[1:]
}
for len(right) != 0 {
result = append(result, right[0])
right = right[1:]
}
return result
}
4、归并排序总结
归并排序:申请已排好序列的大小的空间,两个指针,最初位置分别为两个已经排序序列的起始位置,比较,移动数据,指针移动下一位置,重复直到某一指针到序列尾。归并排序是稳定的排序算法。
5、其他排序算法
这里给出十大经典排序算法中的其他排序算法文章链接供参考、学习
冒泡排序:https://blog.csdn.net/weixin_43876206/article/details/89488568
选择排序:https://blog.csdn.net/weixin_43876206/article/details/89488999
插入排序:https://blog.csdn.net/weixin_43876206/article/details/89489021
希尔排序:https://blog.csdn.net/weixin_43876206/article/details/89490445
快速排序:https://blog.csdn.net/weixin_43876206/article/details/89501766
如有问题、想法,欢迎在此文章下面留言讨论。