使用遗传算法求解TSP(旅行商)问题
目录
- 题目要求
- 算法流程图
- 步骤描述
- 代码实现(MATLAB)
- 主文件
- 种群初始化函数(initmatrixpop.m)
- 距离m*m矩阵初始化函数(initdistance.m)
- 计算适应度函数(fitness.m)
- 交叉函数(cross.m)
- 选择函数(choose.m)
- 变异函数(variate.m)
- 运行结果
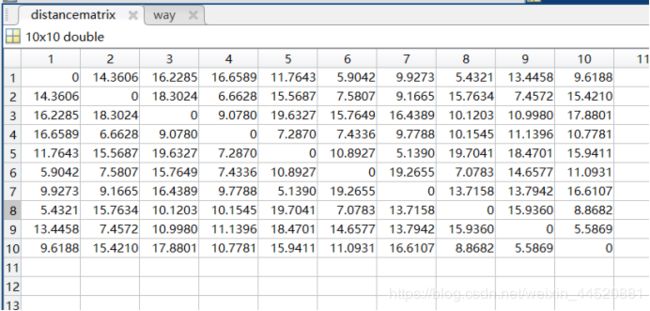
- 距离矩阵
- 最短路程变化图
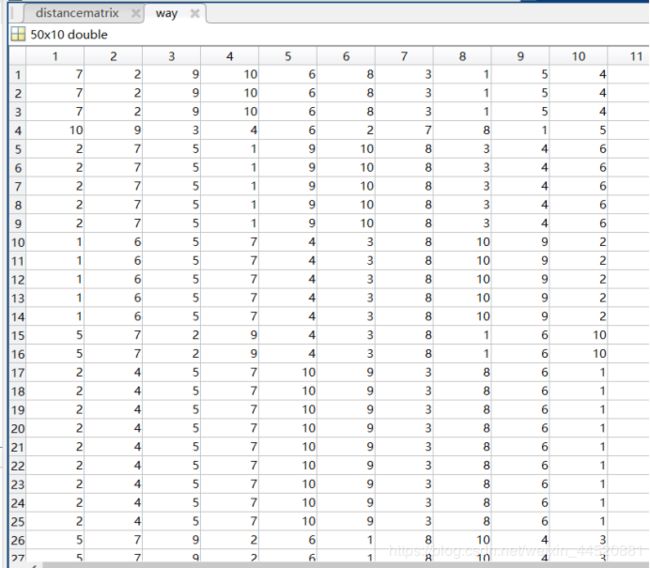
- 每代的最优路径
- 参考资料
题目要求
TSP问题即:已知N个城市之间的相互距离,某一个旅行商从某个城市出发访问每个城市一次,最后回到出发城市,求最短路径。使用遗传算法求解。
- 随机生成N个城市间的链接矩阵;
- 指定起始城市;
- 给出每一代的最优路线和总路线长度;
- 以代数T作为结束条件,T>=50.
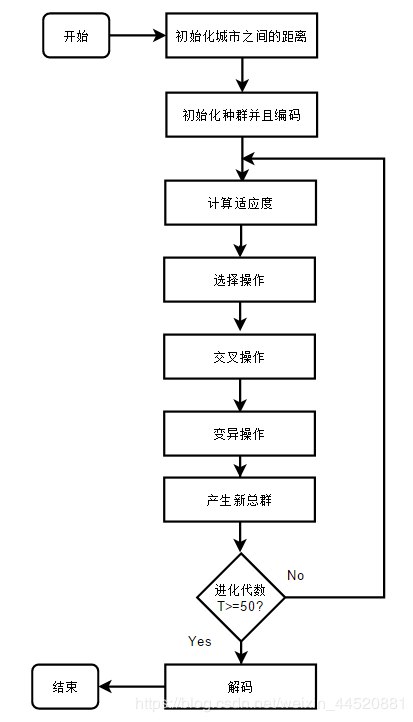
算法流程图
步骤描述
- 初始化城市距离
通过给定城市的个数N、城市之间的最小、最大距离,通过MATLAB的rand函数生成一个N*N的距离矩阵(其对角线距离默认为0)。 - 初始化种群并且编码
可以把一个N个城市的旅行回路排列成一个N维向量,用它来表示一个染色体,如[1,2,3,4,5,6,7,8,9,10],带入距离矩阵,即可求出该向量所表示的回路的路程. - 计算适应度
通过适应度函数(求该染色体(回路向量)的路程和的倒数),计算出该回路的适应度值。因此,可以表示:适应度越大的回路(染色体)越优。这是选择操作的依据 - 选择操作
通过适应度函数计算出种群中每个个体的适应度,使用轮盘赌法,进行染色体的选择,适应度值越大的,被选中的概率也就越大。 - 交叉操作
在交叉的过程中,随机生成两个1~N之间的整数,确定父代染色体(回路)的交叉区间,对该区间中的染色体,进行交换,通过一个循环结构依次替换掉其他段重复的编码。 - 变异操作
在变异的过程中,随机生成二个1~N之间的整数,确定变异的位置,交换该回路(染色体)中的这两个位置的值。 - 产生新总群
通过以上操作,将会产生N个新的个体(由选择率决定),为了确保种群中的个体数目维持稳定,通过对原总群的适应度值排序,这时(淘汰)删除适应度值低的N个个体,再将新个体插入到总群中,即可以产生新的总群。
代码实现(MATLAB)
主文件
tripnum = 10; %城市的数量为
distancemin = 5; %城市之间的最短距离
distancemax = 20; %城市之间的最长距离
%distancematrix = initdistance(tripnum,distancemin,distancemax); %初始化城市之间的距离矩阵
popnum = 80; %种群数量
%popmatrix=initmatrixpop(popnum,tripnum); %初始化种群矩阵
%fit = fitness(popmatrix,distancematrix); %生成种群对应的适应度列向量
chprob = 0.5; %选择的概率为0.5
%choosed = choose(popmatrix,fit,chprob); %选择父代
crprob = 0.9; %交叉概率为0.5
%crosed = cross(choosed,crprob); %使被选择的个体交叉
vprob = 0.05; %变异概率
%variation = variate(crosed,vprob); %变异操作
T = 1; %代数
y = []; %用来存放每一代的最优路径
way = [];
distancematrix = initdistance(tripnum,distancemin,distancemax); %初始化城市之间的距离矩阵
popmatrix=initmatrixpop(popnum,tripnum); %初始化种群矩阵
while(T<=50)
fit = fitness(popmatrix,distancematrix); %生成种群对应的适应度列向量
choosed = choose(popmatrix,fit,chprob); %选择父代
crosed = cross(choosed,crprob); %使被选择的个体交叉
variation = variate(crosed,vprob); %变异操作
[L,~] = size(variation); %新子代的个数
[~,xiabiao] = sort(fit); %按从小到大顺序输出下标
y=[y,1/fitness(popmatrix(xiabiao(end),:),distancematrix)]; %适应度最大那行的总路程
way = [way;popmatrix(xiabiao(end),:)]; %每一代的最短路线
popmatrix(xiabiao(1:L),:) = variation; %把适应度最小的L个替换掉
T = T+1;
end
x = 1:50;
plot(x,y);
xlabel('代数T');
ylabel('最短路程');
title('最短路程随代数变化的关系');
disp(way)
种群初始化函数(initmatrixpop.m)
function pathpop = initmatrixpop(m,n)
%%产生初始化种群,pathpop是产生的初始种群矩阵
%m为矩阵pathpop的行数,即种群个数
%n为列数,城市的个数,一列表示一个路线.
pathpop = [];
for i = 1:m
pathpop = [pathpop;randperm(n)]; %每次产生一行1-n的随机序列
end
end
距离m*m矩阵初始化函数(initdistance.m)
function distancematrix = initdistance(m,min,max)
%%随机生成城市距离m*m矩阵
%m表示城市的个数,[min,max]为产生的矩阵的城市之间的距离范围
distancematrix = tril(((max-min)*rand(m) + min),-1);
distancematrix = distancematrix + distancematrix';
%产生对角矩阵distancematrix,对角线上的元素都为0
end
计算适应度函数(fitness.m)
function fitness = fitness(pop,distance)
%%计算个体的适应度值的大小(路程总合的倒数)
%fitness为列向量,长度为个体数目,对应的值为适应度函数值
%initpop为初始种群矩阵,initdistance为初始距离矩阵
[m,n] = size(pop); %m为个体数目,n为城市数字
fitness = zeros(m,1);
for i = 1:m
for j = 1:n-1
fitness(i) = fitness(i) + distance(pop(i,j),pop(i,j+1));
%序列中相邻了两个之间的距离累加
end
fitness(i) = fitness(i) + distance(pop(i,j),pop(i,1));
%末尾到起点的距离
end
fitness = 1./fitness;
end
交叉函数(cross.m)
function newson = cross(chose,prob)
%交叉函数,newson为产生的新子一代
%chose为选择以后的子代,prob为交叉发生的概率
[m,n] = size(chose);
m = (m-mod(m,2)); %将个体修正为偶数个,从而两两交叉
for i = 1:2:m
if prob > rand %判断概率执行交叉操作
if sum(chose(i,:) ~= chose(i+1,:)) %若两个父亲相同,则不交叉
c = unidrnd(n,1,2); %随机产生两个1-n之间的自然数
a = min(c); %[a,b]为交叉范围,a与b可以相同
b = max(c);
for j = a:b
x = chose(i,:); %复制两个交叉矩阵,用来当做中间交换变量
y = chose(i+1,:);
chose(i,j) = y(j);
chose(i+1,j) = x(j);
r1 = find(x == y(j));
chose(i,r1) = x(j);
r2 = find(y == x(j));
chose(i+1,r2) = y(j);
end
end
end
end
newson = chose(1:m,:);
end
选择函数(choose.m)
function choosed = choose(pop,fitness,prob)
%%选择函数,采用轮盘赌法,choosed返回被选择的个体矩阵.
%pop为待选择的总群
%prob为选择概率
%fitness为pop总群对应的适应度
[m,n] = size(pop); %m为个体数
choosed = [];
choosenum = length(find(rand(1,m)= rand*max); %找到轮盘转到的区域g(1)取得位置
number = [number,g(1)]; %轮盘赌法选择一次
end
choosed = pop(number,:);
end
变异函数(variate.m)
function newson = variate(newson,prob)
%变异操作,使被交叉的个体变异为variateson
%newson为可能发生变异的个体
%prob为变异率
[m,n] = size(newson);
for i = 1: m
if prob >= rand
r = randperm(n,2);
newson(i,[r(1),r(2)]) = newson(i,[r(2),r(1)]);
end
end
end
运行结果
距离矩阵
最短路程变化图
每代的最优路径
参考资料
《MATLAB在数学建模中的应用》