前言
第二次\(NOI\)赛制模拟赛,虽然这次考试还是水炸了,但是还算有进步。(疯狂\(\%\%\%\%\)lc大佬)
NO.1 翻转游戏(简单版)
Descrption
翻转游戏是在一个 \(4\times 4\) 的正方形上进行的,在正方形的 \(16\) 个格上每个格子都放着一个双面的物件。每个物件的两个面,一面是白色,另一面是黑色,每个物件要么白色朝上,要么黑色朝上,每一轮你只能翻 \(3\) 至 \(5\) 个物件,从而由黑到白的改变这些物件上面的颜色,反之亦然。每一轮被选择翻转的物件遵循以下规则:
从 \(16\) 个物件中任选一个。
翻转所选择的物件的同时,所有与它相邻的左方物件、右方物件、上方物件和下方物件(如果有的话),都要跟着翻转。
以下为例:
bwbw
wwww
bbwb
bwwb
这里 \(b\) 表示该格子放的物件黑色面朝上、\(w\) 表示该格子放的物件白色朝上。如果我们选择翻转第三行的第一个物件,那么格子状态将变为:
bwbw
bwww
wwwb
wwwb
游戏的目标是翻转到所有的物件白色朝上或黑色朝上。你的任务就是写一个程序来求最少的翻转次数来实现这一目标。
Input
输入文件包含 \(4\) 行,每行 \(4\) 个字符,每个字符 \(w\) 或 \(b\) 表示游戏开始时格子上物件的状态。
Output
输出文件仅一个整数,即从给定状态到实现这一任务的最少翻转次数。如果给定的状态就已经实现了目标就输出 \(0\),如果不可能实现目标就输出: \(Impossible\)。
Sample Input
bwwb
bbwb
bwwb
bwww
Sample Output
4
分析
这个题是简单版的,矩阵的范围就是固定的\(4 \times 4\),所以就可以逐层枚举状态。只要上一行的状态确定下来了,那么第二行,第三行,第四行的状态就全部都确定下来了。我们要做的就是把矩阵都改为\(b\)或者\(w\),然后找出这两种里最小步数即为答案。每次的修改就是转换一个数字,很容易实现。我们只需要一层一层修改,最后再判定是否可以让矩阵合法即可。第一行直接修改就行,后边的要根据上一行的状态进行修改,具体见代码注释。
代码
#include
using namespace std;
const int maxn = 9;
const int Inf = 1<<16;
char s[maxn][maxn];
char tem[maxn][maxn];
int ans = Inf;
void gai(char &ch){//把当前点的状态改变,写成函数容易理解。
if(ch == 'b')ch = 'w';
else if(ch == 'w')ch = 'b';
}
int cnt;
void genggai(int x,int y){//更改一次就把次数cnt++,然后当前点和上下左右都进行更改。
cnt++;
gai(tem[x][y]);
gai(tem[x][y+1]);
gai(tem[x][y-1]);
gai(tem[x+1][y]);
gai(tem[x-1][y]);
}
void dp(int x,char ch){//把矩阵全部转换为ch
memcpy(tem,s,sizeof(s));//复制矩阵
cnt = 0;//初始化次数
for(int i=1;i<=4;++i){//枚举第一行四列的状态
if(x & (1<<(i-1))){//x状态的需要翻转第i个,那么就翻转
genggai(1,i);
}
}
for(int i=2;i<=4;++i){//枚举2到4行
for(int j=1;j<=4;++j){//枚举每一列
if(tem[i-1][j] != ch){//当前列上一行不是ch,那么这个点需要翻转
genggai(i,j);
}
}
}
for(int i=1;i<=4;++i){//枚举第四行
if(tem[4][i] != ch){//不符合条件就return
return;
}
}
ans = min(ans,cnt);//记录最小步数
}
int main(){
for(int i=1;i<=4;++i){
scanf("%s",s[i]+1);
}
for(int i=0;i<=15;++i){//枚举每一个状态
dp(i,'b');//b和w都要翻转一遍,然后记录最小值
dp(i,'w');
}
if(ans == Inf){//ans没更改则没有符合条件的情况
printf("Impossible");
return 0;
}
printf("%d\n",ans);
}
注意!!!
我又双叒叕来模liuchang大佬了,他这道题的暴力枚举状压dp实在是妙极了,下边贴一个代码自行体会
代码(大佬)
#include
using namespace std;
const int maxn=5;
int f[1<=0;i--){
for(int j=(1<<4)-1;j>=0;j--){
for(int k=(1<<4)-1;k>=0;k--){
for(int m=(1<<4)-1;m>=0;m--){
for(int d=1;d<=4;d++){
if(d==1){
for(int n=1;n<=4;n++){
if(n==1){
int now=i^(1<<(n-1));
now=now^(1< NO.2 抢掠计划
题目描述
\(Siruseri\) 城中的道路都是单向的。不同的道路由路口连接。按照法律的规定,在每个路口都设立了一个 \(Siruseri\) 银行的 \(ATM\) 取款机。令人奇怪的是,\(Siruseri\) 的酒吧也都设在路口,虽然并不是每个路口都设有酒吧。
\(Banditji\) 计划实施 \(Siruseri\) 有史以来最惊天动地的 \(ATM\) 抢劫。他将从市中心出发,沿着单向道路行驶,抢劫所有他途径的 \(ATM\) 机,最终他将在一个酒吧庆祝他的胜利。
使用高超的黑客技术,他获知了每个 \(ATM\) 机中可以掠取的现金数额。他希望你帮助他计算从市中心出发最后到达某个酒吧时最多能抢劫的现金总数。他可以经过同一路口或道路任意多次。但只要他抢劫过某个 \(ATM\) 机后,该 \(ATM\) 机里面就不会再有钱了。 例如,假设该城中有 \(6\) 个路口,道路的连接情况如下图所示:
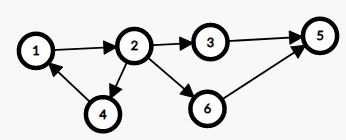
市中心在路口 \(1\),由一个入口符号 \(→\) 来标识,那些有酒吧的路口用双圈来表示。每个 \(ATM\) 机中可取的钱数标在了路口的上方。在这个例子中,\(Banditji\) 能抢劫的现金总数为 \(47\),实施的抢劫路线是:\(1-2-4-1-2-3-5\)。
输入格式
第一行包含两个整数 \(N,M\)。\(N\) 表示路口的个数,\(M\) 表示道路条数。
接下来 \(M\) 行,每行两个整数,这两个整数都在 \(1\) 到 \(N\) 之间,第 \(i+1\) 行的两个整数表示第 \(i\) 条道路的起点和终点的路口编号。
接下来 \(N\) 行,每行一个整数,按顺序表示每个路口处的 \(ATM\) 机中的钱数 \(a_i\) 。
接下来一行包含两个整数 \(S,P\)。\(S\) 表示市中心的编号,也就是出发的路口。\(P\) 表示酒吧数目。
接下来的一行中有 \(P\) 个整数,表示 \(P\) 个有酒吧的路口的编号。
输出格式
输出一个整数,表示 \(Banditji\) 从市中心开始到某个酒吧结束所能抢劫的最多的现金总数。
输入输出样例
输入
6 7
1 2
2 3
3 5
2 4
4 1
2 6
6 5
10
12
8
16
1
5
1 4
4 3 5 6
输出
47
说明/提示
对于 \(50\%\) 的数据,保证 \(N, M \le 3000\)。
对于 \(100\%\) 的数据,保证 \(N, M \le 5\times 10^5\) ,\(0 \le a_i \le 4000\)。保证可以从市中心沿着 \(Siruseri\) 的单向的道路到达其中的至少一个酒吧。
分析
因为可以重复走一些路,那么很容易就可以想到走过所有的环肯定是价值最大的。那么就能想到用\(Tarjan\)缩点。然后就是取价值的问题了,这个题每个地方都有一个点权,我们可以把它当做边权,然后跑一遍\(spfa\)最长路,求出缩点之后最长的一个边,然后输出答案即可。(这个题也是我唯一一个一遍\(AC\)的题)
代码
#include
using namespace std;
const int maxn = 5e5+10;
#define ll long long//一定要开long long 啊!!!
struct Node{//建边的结构体。
int v,next;
}e[maxn<<1],ec[maxn<<1];
int hc[maxn];
int sta[maxn],top,num,cnt;
ll siz[maxn],low[maxn],dfn[maxn];
int c[maxn];
ll tot2;
vectorscc[maxn];
int head[maxn];
ll dis[maxn],vis[maxn],a[maxn];
ll tot;
void Add(int x,int y){//一开始的建边
e[++tot].v = y;
e[tot].next = head[x];
head[x] = tot;
}
void Add2(int x,int y){//缩点后建边
ec[++tot2].v = y;
ec[tot2].next = hc[x];
hc[x] = tot2;
}
void Tarjan(int x){//Tarjan缩点,求强连通分量
sta[++top] = x;
dfn[x] = low[x] = ++num;
vis[x] = 1;
for(int i=head[x];i;i = e[i].next ){
int v= e[i].v;
if(!dfn[v]){
Tarjan(v);
low[x] = min(low[x],low[v]);
}
else if(vis[v]){
low[x] = min(dfn[v],low[x]);
}
}
if(low[x] == dfn[x]){
cnt++;
int y;
while(1){
y = sta[top--];
c[y] = cnt;
siz[cnt]++;
vis[y] = 0;
scc[cnt].push_back(y);
if(x == y)break;
}
}
}
ll a1[maxn];
queueq;
void spfa(int x){//spfa求最长路
q.push(x);
dis[x] = a1[x];
vis[x] = 1;
while(!q.empty()){
int y=q.front();
q.pop();
vis[y] = 0;
for(int i=hc[y];i;i = ec[i].next){
int v= ec[i].v;
if(dis[v] < dis[y] + a1[v]){
dis[v] = dis[y]+a1[v];
if(!vis[v]){
q.push(v);
vis[v] = 1;
}
}
}
}
}
int n,m;
int jb[maxn];
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;++i){//开始建边
int x,y;
scanf("%d%d",&x,&y);
Add(x,y);
}
for(int i=1;i<=n;++i){//点权输入
scanf("%lld",&a[i]);
}
int p,s;
scanf("%d%d",&s,&p);
for(int i=1;i<=p;++i){//输入酒吧位置
scanf("%d",&jb[i]);
}
for(int i=1;i<=n;++i){//缩点
if(!dfn[i])Tarjan(i);
}
for(int x=1;x<=n;++x){
for(int i=head[x];i;i=e[i].next){//不在一个强连通分量里就建边,缩完点的图就再建一个邻接表
int y = e[i].v;
if(c[x] == c[y])continue;
Add2(c[x],c[y]);
}
}
for(int i=1;i<=n;++i){//初始化每个强连通分量的点权
a1[c[i]]+=a[i];
}
spfa(c[s]);//从市中心所在的强连通分量开始
ll ans = 0;
for(int i=1;i<=p;++i){
if(dis[c[jb[i]]] > ans){//统计最大值
ans = dis[c[jb[i]]];
}
}
printf("%lld\n",ans);
}
NO.3 测绘
Descrption
为了研究农场的气候,\(Betsy\)帮助农夫\(John\)做了 \(N(1≤N≤100)\) 次气压测量并按顺序记录了结果\(M_1,M_2,…,M_N(1≤M_i≤1,000,000)\).
\(Betsy\)想找出一部分测量结果来总结整天的气压分布. 她想用\(K(1≤K≤N)\)个数\(S_j(1≤S_1
对于任何测量结果子集,每一个非此子集中的结果都会产生误差。总误差是所有测量结果的误差之和。更明确第说, 对于每一个和所有 \(S_j\) 都不同的 \(i\) :
如果 \(i\) 小于 \(S_1\), 误差是: \(2∗|M_i–M_{S_1}|\) ;
如果 \(i\) 在 \(S_j\) 和\(S_j+1\) 之间,误差是: \(|2\times M_i–Sum(S_j,S_{j+1})|\) ;
注:\(Sum(x,y)=M_x+M_y\); (\(M_x\) 和 \(M_y\) 之和) ;
如果 \(i\) 大于 \(S_K\) ,误差为: \(2\times |M_i–M_{S_K}|\) ;
\(Besty\) 给了最大允许的误差 \(E(1≤E≤1,000,000)\) ,找出样本 \(k\) 最小的一部分结果使得误差最多为 \(E\).
Input
第一行:两个数 \(N,E\)(含义如题)。
接下来 \(N\) 行每行一个数表示气压。
Output
输出一行,两个数,第一表示最小的样本数 \(K\),第二个表示这 \(K\) 个样本的最小误差值
Sample Input
4 20
10
3
20
40
Sample Output
2 17
分析
这个题主要是题目费劲死,只要读懂了题目,那么就很好理解了。题目中误差的意思也就是当你选了一个数作为测量误差的数的时候,就是这个数两边所有的数与他作差取绝对值再乘以\(2\)。如果是两个数,就是他们之间的数分别与其作差,然后左右两边都作差,我们就可以用\(pre\)数组处理。\(pre[i][j]\) 表示:原序列中\(M_i,M_j\) 是所选子序列的相邻的两个元素,\(pre[i][j]\)表示 \(i\) 到 \(j\) 之间元素对误差的贡献,枚举 \(k,(i+1≤k≤j−1)\) ,计算\(abs(2\times M_k−M_i−M_j)\) ,显然我们可以 \(n^3\) 暴力枚举预处理出此结果。
\(pre[i][0]\) 记录如果 \(M_i\) 作为序列第一个数,则\(M_1∼M_{i-1}\) 的误差之和,\(pre[i][n+1]\) 记录如果 \(M_i\) 作为所选子序列的最后一个元素,则 \(M_{i+1}∼M_n\) 的误差之和。
状态方程为\(dp[i][j]\)表示前\(j\)个数里选\(i\)个的最小误差,所以状态转移就是:
表示第\(j\)为结尾的数选\(i\)个的值,从选\(i-1\),结尾为\(K\)转移而来。\(dp[i-1][k]\)把 \(k\) 当成了序列的最后一位,所以\(+pre[k][n+1]\) ,所以先减去,此时把 \(i\) 当做了最后一位,所以 \(+pre[i][n+1]\) ,然后加上 \(M_k∼M_i\) 之间的误差 \(pre[k][i]\) 。
代码
#include
using namespace std;
const int maxn = 1e2+10;
const int Inf = 0x3f3f3f3f;
#define ll long long
ll ans;
int pre[maxn][maxn];
ll dp[maxn][maxn];
int n,E;
int a[maxn];
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n>>E;
for(int i=1;i<=n;++i){
cin>>a[i];
}
for(int i=1;i<=n;++i){//预处理从i到j的区间误差贡献
for(int j=i+1;j<=n;++j){
for(int k=i+1;k<=j-1;++k){
pre[i][j] += abs(2*a[k]-a[i]-a[j]);
}
}
for(int j=1;jans1)continue;//选的数大于不更新
if(i NO.4 奖学金
Descrption
猪仙发现人类可以上很多大学,而猪们却没有大学可上。为了解决这个问题,于是他创立了一所大学,取名为猪仙大学。
为了选拔合适的学生入学,他发明了一种学术能力测试(简称 \(CSAT\) ),这种测试的分数异常精确,每头猪的成绩可以用 \(1\) 到 \(2,000,000,000\) 之间的一个整数表示。
猪仙大学的学费很贵(猪仙比较黑),很多猪都负担不起,他们需要申请一些奖学金\((1≤ 奖学金 ≤10000)\)。可是政府并没有为猪准备奖学金,于是所有的预算都必须要从学校自身有限的基金中间扣除(设基金总额为 \(F,0≤F≤2,000,000,000\))。
更槽的事,猪仙大学的只有 \(N(1≤N≤19999)\) 间教室,\(N\) 是一个奇数,而一共有\(C(N≤C≤100,000)\)头猪申请入学,为了让最多的猪接受教育,猪仙打算接受\(N\) 头猪的申请,而且她还想让这些猪 \(CSAT\) 成绩的中位数尽可能地高。
所谓中位数,就是在一堆数字在排序后处在最中间的那个数字,比如 \({3,8,9,7,5}\) 的中位数就是 \(7\)。
给定每头猪的 \(CSAT\) 成绩和打算申请的奖学金数目,以及可以资助的基金总数,确定猪仙接受哪些猪的申请才可以使成绩的中位数达到最大。
Input
第一行:三个用空格分开的整数:\(N,C 和 F\)。
第二行到 \(C+1\) 行:每行有两个用空格分开的整数。第一个数是这头猪的 \(CSAT\) 成绩,第二个数是这头猪想申请的奖学金。
Output
第一行:一个整数,表示猪仙可以得到的最大中位数,如果现有基金不够资助 \(N\) 头猪,则输出$ −1$。
Sample Input
3 5 70
30 25
50 21
20 20
5 18
35 30
Sample Output
35
分析
数据范围这么大,直接枚举区间当然是不可行的,所以我们用一个很巧妙的优化:大根堆。中位数\(a_i\)必须满足 \({n\over 2} + 1 \le i \le c-{n\over 2}\)
\(i = {n\over 2}+1\)时,肯定要选前\(n\over 2\)个分数低且钱少的猪,所以我们可以枚举每一个中位数,用一个维护奖金的大根堆,每枚举完一个中位数,如果当前的奖金比堆顶的小,则交换,维持堆里有\({n\over 2}\)个数,用一个数组 \(f[i]\) 维护如果选 \(a_i\) 为中位数,前 \({n\over 2}\) 个数的最小奖金。
同上,倒序维护,求出 \(g[i]\) 表示,如果选 \(a_i\) 为中位数,则后 \(n^2\) 个数最小奖金。
所以答案为满足 \(f[i]+g[i]+a[i].money \le F\) 的最大的 \(a[i].fenshu\)
代码
#include
using namespace std;
const int maxn = 2e5+210;
priority_queueq;//大根堆
struct Node{
int lev,moy;
}a[maxn];//lev为分数,moy为钱数。
int n,c,F;
int sum = 0;
bool cmp(const Node &a,const Node &b){//sort的排序函数
return a.lev < b.lev;
}
int f[maxn],g[maxn];
int main(){
cin>>n>>c>>F;
for(int i=1;i<=c;++i){
cin>>a[i].lev>>a[i].moy;
}
sort(a+1,a+c+1,cmp);
for(int i=1;i<=n/2;++i){//成绩前n/2的人入队
sum += a[i].moy;//sum记录前二分之i个里的奖金数。大根堆放入。
q.push(a[i].moy);
}
for(int i=n/2+1;i<=c;++i){//f[i]:表示以i为中位数前n/2人的最小奖金
f[i] = sum;
int top = q.top();
if(top>a[i].moy){//奖金小于堆顶则换掉,因为越小越好。
q.pop();
sum -= top;
sum += a[i].moy;
q.push(a[i].moy);
}
}
sum = 0;
for(int i=c;i>=c-n/2+1;--i){//成绩后n/2入队
sum += a[i].moy;
q.push(a[i].moy);
}
for(int i=c-n/2;i>=1;--i){//g[i]是i为中位数是后n/2人最小奖金
g[i] = sum;
int top = q.top();
if(top>a[i].moy){//同上,如果小,就换
q.pop();
sum -= top;
sum += a[i].moy;
q.push(a[i].moy);
}
}
for(int i=c-n/2;i>=n/2+1;--i){//枚举每一种中位数的可能
if(g[i]+f[i]+a[i].moy <= F){//因为是从大到小枚举的,所以满足情况就直接输出结束。
cout<