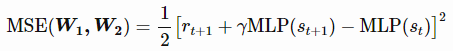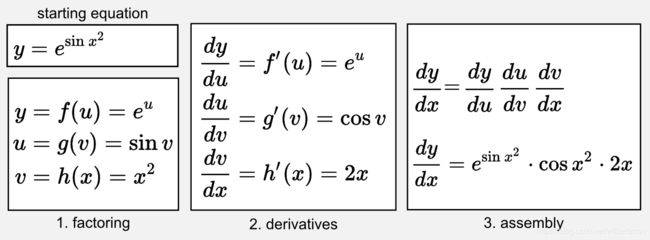剖析强化学习 - 第八部分
作者:Massimiliano Patacchiola
在上一篇文章中,我介绍了函数逼近作为在强化学习设置中表示效用函数的方法。我们使用的简单逼近器基于特征的线性组合,并且它非常有限,因为它无法模拟复杂的状态空间(如XOR网格世界)。在这篇文章中,我将介绍人工神经网络作为非线性函数逼近器,向您展示如何使用神经网络来模拟效用函数。我将从名为Perceptron 的基本架构开始,然后转向称为多层感知机(MLP)的标准前馈模型。此外,将介绍(大多数时候)基于神经网络策略的策略梯度方法。我将使用纯Numpy来实现网络和更新规则,这样你就可以有一个浅显的代码来学习。这篇文章很重要,因为它可以使你理解深度强化学习中使用的深层模型(例如卷积神经网络),我将在下一篇文章中介绍。
这篇文章的参考文献是Sutton和Barto的书 “Generalization and Function Approximation”的第8章,最近该书的第二版已经发布,你可以在DuckDuckGo上轻松找到免费预印版。此外,一个很好的资源是David Silver课程的视频课程7。在Goodfellow、Bengio和Courville撰写的“深度学习”一书中,对神经网络进行了更广泛的介绍。
我想以神经网络的简史开始这篇文章,向您展示第一个神经网络如何具有前一篇文章中讲述的线性模型的相同限制,然后将介绍称为多层感知机(MLP)的标准神经网络,我将向您展示如何使用它来模拟任何效用函数。这个帖子与之前的帖子相比可能很难懂,但我建议你仔细研究,因为使用神经网络作为函数逼近器是支持现代RL方法的基础。
感知机历史
1957年,美国心理学家弗兰克·罗森布拉特(Frank Rosenblatt)在纽约康奈尔航空实验室会议上发表了题为“感知机:感知和自动识别”的报告。Perceptron不是一个软件,它是在一个定制的硬件(像衣柜一样大)中实现的,它可以区分两种类型的标记卡,第一类卡片标记在左侧,而第二类卡片标记在右侧,400个光电管的网格能够定位标记并激活机械继电器,调整Perceptron的参数并不像今天那么容易。在pyTorch/Tensorflow中,我们只是定义了一堆变量,然后我们搜索最佳组合。在硬件实现中,要调整的参数是通过电动机调节的物理手柄(电位计)来实现的。
下面为您奉上我找到的“纽约时报”的原始文章,它登载了Rosenblatt及其工作人员对Perceptron的官方介绍:
正如你所读到的那样,Perceptron的力量有点被高估了,特别是谈论到“会意识到它们的存在”的人造大脑(我们可以从这里开始讨论意识究竟是什么,但它需要另一个博客系列文章)。但是,Rosenblatt做出的另外一些预测是正确的:
“后来的感知机将能够识别人并叫出他们的名字,并且立即将演讲从一种语言翻译成另一种语言”
经过了数十年的时间这终于成为了现实。从技术角度来看,Perceptron是什么?您可能会惊讶地发现Perceptron是一个线性函数逼近器,就像上一篇文章中描述的那样。让我们试着将这一点正式化。输入到Rosenblat的感知机是400个二进制光电管,我们可以建模为矢量x =(x1,x2 ,,..., x400),输出是电压,我们称之为y。输入和输出之间的连接是一系列电线和电位计,我们可以通过另一个包含400个实数值(电位器的电阻)的矢量w来建模。我说Perceptron是一个线性系统,和上一篇文章中描述的线性模型完全一样,我们可以将它定义为两个向量之间的点积![]() 。但是,有一个中间步骤:使用称为
。但是,有一个中间步骤:使用称为![]() 的激活函数将加权和的结果作为输入并生成输出y:
的激活函数将加权和的结果作为输入并生成输出y:
我们还可以使用一个名为![]() 的附加偏置单元和它的权重
的附加偏置单元和它的权重![]() ,可以将偏置附加到向量x,同时将偏置权重附加到向量w。偏置单元已经在以前的帖子中被广泛讨论,如果你不记得我们为什么需要它,我建议你再回去看看。最后一个等式是Perceptron的最终形式,以图形方式将Perceptron表示为有向图可以帮助理解,其中每个节点是单元(或神经元),每个边是权重(或突触)。关于名称惯例,社区中没有明确的规则,我个人更喜欢使用术语单元(unit)和权重(weight)而不是神经元和突触,以避免与生物学术语相混淆。
,可以将偏置附加到向量x,同时将偏置权重附加到向量w。偏置单元已经在以前的帖子中被广泛讨论,如果你不记得我们为什么需要它,我建议你再回去看看。最后一个等式是Perceptron的最终形式,以图形方式将Perceptron表示为有向图可以帮助理解,其中每个节点是单元(或神经元),每个边是权重(或突触)。关于名称惯例,社区中没有明确的规则,我个人更喜欢使用术语单元(unit)和权重(weight)而不是神经元和突触,以避免与生物学术语相混淆。
下图代表Rosenblatt 的感知机。只有在卡片上标识了标记时,才会触发400个光电管,每个光电管都可以被认为是Perceptron的输入。在这里,我使用绿色表示神经元的活动单元(状态=1),红色表示非活动单元(状态= 0),橙色表示具有未定义状态的单元。当我说“未定义状态”时,我的意思是该单元的输出尚未计算,例如,这是在计算加权和及应用转换函数之前输出单元y的状态。在图像中你必须注意到偏置单元始终处于活动状态,在上一篇文章中,我们使用这个技巧用于增加模型中的偏置。
正如我上面所说,线性逼近器和感知机之间的唯一区别是激活函数![]() 。原始感知机使用符号函数(sign function)生成类型为0或1的二进制输出,符号函数引入了一个问题,使用符号函数不可能应用梯度下降,因为此函数不可微,即你应该知道的一个重要细节是基于梯度的技术(例如反向传播)此时是未知的。
。原始感知机使用符号函数(sign function)生成类型为0或1的二进制输出,符号函数引入了一个问题,使用符号函数不可能应用梯度下降,因为此函数不可微,即你应该知道的一个重要细节是基于梯度的技术(例如反向传播)此时是未知的。
Rosenblatt 是如何训练Perceptron的?这是个很有意思的部分,Rosenblatt使用了一种Hebbian学习形式。心理学家Donald Hebb在几年前(1949年)发表了题为“行为的组织”的著作,他从神经连接模式的角度解释了认知过程,原理很容易掌握:当两个神经元同时激活时,它们的连接得到加强。Ronsenblat在定义Perceptron的更新规则时受到了这项工作的启发,更新规则直接管理训练阶段的三种可能结果,并重复一定数量的epoch:
- 如果输出y是正确的,保留权重w不变
- 如果输出y不正确(0而不是1),增加输入向量x到权重向量w中
- 如果输出y不正确(1而不是0),从权重向量w中减去输入向量x
更新规则的几何解释可以帮助您了解正在发生的事情。w是一个向量,意味着我们可以在三维空间中想象这个向量,向量的起点位于轴的原点,而向量的终点位于其值指定的坐标处,所有输入向量的集合也可以被认为是占据相同三维空间的一部分的一组向量。我们在更新期间正在做的是移动权重向量来改变其终点坐标,矢量的最佳位置在锥体内(其顶点在原点处),其中始终满足学习规则的第一标准。换句话说,当权重向量达到该锥体时,不再触发更新规则的第二和第三个条件。
在Python中实现Perceptron及其更新规则非常简单,下面是一个例子:
def perceptron(x_array, w_array):
'''Perceptron model
Given an input array and a weight array
it returns the output of the model.
@param: x_array a binary input array
@param: w_array numpy array of weights
@return: the output of the model
'''
import numpy as np
#Dot product of input and weights (weighted sum)
z = np.dot(x_array, w_array)
#Applying the sign function
if(z>0): y = 1
else: y = 0
#Returning the output
return y
def update_rule(x_array, w_array, y_output, y_target)
'''Perceptron update rule
Given input, weights, output and target
it returns the updated set of weights.
@param: x_array a binary input array
@param: w_array numpy array of weights
@param: y_output the Perceptron output
@param: y_target the target value for the input
@return: the updated set of weights
'''
if(y_output == y_target):
return w_array #first condition
elif(y_output == 0 and y_target == 1):
return x_array + w_array #second condition
elif(y_output == 1 and y_target == 0)
return x_array - w_array #third condition在上一篇文章中,我提到线性逼近器是有限的,因为它们只能用于线性可分的问题,同样的考虑适用于Perceptron。从历史上看,研究界并未意识到这个问题,Perceptron的工作持续了数年最终取得了成功。Widrow和Hoff于1960年在斯坦福大学获得的结果引起了人们的兴趣,当时Perceptron名为ADALINE。ADALINE网络有多个输入和输出,输出上使用的激活函数是线性函数,更新规则是Delta规则。Delta规则是基于梯度下降过程的反向传播的特例,当时这是一个重要的成功,但主要问题仍然存在:ADALINE仍然是线性模型,Delta规则不适用于非线性设置。
问题的出现: 1969年出版了一本名为“Perceptrons: an introduction to computational geometry” 的书,在书中,作者Marvin Minsky和Seymour Papert在数学上证明了类似Perceptron的模型只能解决线性可分的问题,并且它们不能应用于非线性数据集,如XOR数据集。在上一篇文章中,我仔细选择了XOR网格世界作为非线性问题的一个例子,向您展示线性逼近器无论如何无法描述这个世界的效用函数,这就是Minsky和Papert在他们的书中所证明的。所谓的XOR事件标志了Perceptron时代的结束,人工神经网络项目的资金逐渐消失,只有少数研究人员继续研究这些模型。
复兴(多层感知机)
冬天过后,春天回来了!直到1985年我们才看到神经网络的复苏,Rumelhart,Hinton和Williams发表了一篇题为“通过误差传播学习内部表征”的文章,该文章使用广义delta规则来训练具有多层的感知机。多层感知机(MLP)是具有一个或多个中间层的经典感知机的扩展,作者通过实验证实,使用附加层(称为隐藏层)和新的更新规则,网络能够解决XOR问题,这一结果再次点燃了人们对神经网络的研究热情。作者说:
“简而言之,我们相信我们已经回答了Minsky和Papert的挑战,并且发现了一个足够强大的学习成果,以证明他们对多层机器学习的悲观态度是错误的。”
MLP的经典形式基于输入层、隐藏层和输出层,层之间使用的转换函数通常是sigmoid,误差函数可以被定义为输出和标签之间的均方误差(MSE)。MLP的每一层可以表示为输入向量x和权重矩阵w的乘积,其结果加上偏置后传递给激活函数,生成输出向量y,这些操作等效于用于线性逼近器中的输入值的加权和。与Perceptron类似,我们可以将MLP表示为有向图,在下图中(我建议您仔细查看)您可以看到MLP是如何组装的。与Perceptron相关的主要区别是隐藏层h是通过输入向量x和权重矩阵w1的乘积得到的,权重求和后的数组z传递给sigmoid激活函数,您应该注意偏置项是如何嵌入到输入和隐藏向量中的。再次重复相同的过程,隐藏层的输出与权重矩阵w2相乘,传递给一个sigmoid函数,最终输出向量y。在神经网络术语中,从输入x开始到输出y的过程被称为前向传播(forward pass)。
为什么MLP不是线性模型?这是至关重要的一点。只有当我们使用非线性激活函数(例如,sigmoid、tanh、ReLU等)时,才能很容易地证明MLP是非线性逼近器。如果我们用线性激活函数替换sigmoid,那么我们的MLP就会退化成Perceptron。关于MLP的另一个有趣的事实是,给定足够数量的隐藏神经元,它可以逼近任何连续函数,这被称为通用逼近定理(universal approximation theorem),它由George Cybenko于1989年被证明。
反向传播(概述)
MLP背后的主要创新是基于反向传播的更新规则。反向传播的想法当时并不是全新的,但经过一段时间后才发现可以将其应用于前馈网络。正如就像上一篇文章中描述的那样,每当我们想要训练函数逼近器时,我们需要两件事:
- 一个是误差度量,用于给出评估器的输出与目标之间的距离。
- 一个是更新规则,用于设置评估器的参数以减少误差。
由于神经网络是函数逼近器,因此它们也需要这两个部分,所述误差度量仍然由网络输出和目标值之间的均方误差(MSE)给定。由于我们在每个步骤之后使用TD(0)进行自助(bootstrapping)和在线更新,因此该误差度量将减少为:
使用自助目标效用函数![]() 由MLP本身在t + 1估算,并通过折扣因子γ加权后加上奖励,形成以下表达式:
由MLP本身在t + 1估算,并通过折扣因子γ加权后加上奖励,形成以下表达式:
该更新规则仍是一个梯度下降过程的应用,在神经网络的情况下被称为反向传播(backpropagation)。有必要说明,自助忽略了对目标的影响,只考虑了 ![]() 处针对权重w1 和w2估计的偏导数(半梯度法)。如果你不想进入反向传播的数学细节,这就足够了,你可以跳过下一节。
处针对权重w1 和w2估计的偏导数(半梯度法)。如果你不想进入反向传播的数学细节,这就足够了,你可以跳过下一节。
反向传播(一些数学公式)
可以将反向传播视为链式法则(chain rule)在网络的不同层上的迭代应用。如果你想理解反向传播背后的数学,你应该复习下微积分。在这里,我只能根据我在本科生入门课程中使用的材料给你一个快速回顾。首先,必须知道什么是导数以及如何计算最重要函数的导数(例如sin、cos、指数、多项式)。链式法则是一个简单的迭代过程,允许计算函数组合的导数,迭代过程包括在组合中移动并计算过程中遇到的所有函数的导数。在这里,我将向你展示一个应用于具有单个变量x的等式的链式法则的示例:
正如您所看到的,这个想法是(1)将初始方程式分解为不同的部分,然后(2)计算每个部分的导数,最后(3)乘以每个部分。直观地,您可以看到反向传播是打开一组黑色中国盒子(Chinese boxes)直到出现红色盒子的过程。在我们的例子中,红色盒子是变量x并且要打开的黑色盒子是我们必须得到的最终需要计算的各个式子。
链式法则如何应用到神经网络?这是很多人都在一直努力的事情。将神经网络视为一个神奇的盒子,你可以在其中推送一个数组,并获得另一个数组,推送输入,获得输出,输入和输出可以有不同的大小。例如在我们的Perceptron中,输入数组由400个值组成,输出是单个值,这在技术上是一个标量场(scalar field)。在我们的MLP示例中,提供一个表示世界状态的数组,我们将得到一个输出,表示该状态的效用(作为单个值),或每个可能的操作(作为数组)的效用。现在,神经网络不是一个神奇的盒子,输出y是通过一系列的操作获得的。如果你仔细看看上一节的MLP方案,你可以反向从y到h再从h到x,最后,y通过将sigmoid应用于h的加权和及一组权重来获得,而h使用x的加权和及第一个权重矩阵以类似的方式获得。这个长链操作是多个函数的组合,根据定义,我们可以将链式法则应用于它。
哪些是神经网络中的变量?在神经网络中,我们需要估计的不只一个变量,我们网络的变量(或未知数)是连接单元的权重,我们的目标是找到更好地代表实际效用函数的权重集。与单个变量微积分(如上面的链式法则示例中使用的微积分)不同,神经网络是多变量微积分(multivariable equation)。例如,您可以将Rosenblatt的Perceptron视为具有400个未知数的多变量微积分。在多变量微积分中,我们不考虑导数,而是考虑梯度(gradient),我在上一篇文章中已经写过关于梯度的内容。处理多变量微积分不应该吓到你,因为我们的链式法则仍然有效,但我们现在需要使用偏导数(partial derivatives)而不是标准导数。给出误差函数E我们必须寻找变量集w1 和w2,这意味着我们一直计算导数(打开中国盒子,或者俄罗斯套娃),直到解开它们为止。在下图中,您可以找到MLP过程的数学描述,其中以向量x作为输入,向量y作为输出,两组权重w1(在输入层和隐藏层之间)和w2(在隐藏层和输出层之间)。这些分量的加权和产生两个数组z1和z2,并传递给两个激活函数h =φ(z1)和y =φ(z2)。请记住,链的最后一个元素是误差函数E,出于这个原因E是链式法则的起点。
您可以注意到反向传播的使用非常有效,因为它允许我们重用在后面的层中计算的部分偏导数,以便计算先前层的导数。此外,所有这些操作都可以使用矩阵向量的形式,并且可以在GPU上轻松并行化计算。
反向传播返回的是什么?反向传播找到未知的梯度向量。在我们的MLP中,反向传播找到两个向量,一个是权重w1另一个是权重w2。很好,但我们应该如何使用这些向量?如果您记得上一篇文章中的梯度向量是向上指向误差曲面的向量,这意味着它向我们显示了我们应该移动到哪里以便到达函数的顶部。然而,在这里我们感兴趣的是向下,因为我们想要最小化误差(最终我们做梯度下降),改变梯度前面的符号可以很容易地实现这种方向的变化。
现在,知道移动权重的方向是不够的,我们需要知道我们必须向这个方向移动多少。您必须记住,特定点处函数的陡度由梯度向量的大小给出。在线性代数中,您应该知道将矢量乘以标量会改变矢量的大小,这个标量称为学习率。找到最佳学习率并不容易,研究人员通常使用线性衰减来降低学习率。今天有一些技术(例如Adagrad、Adam、RMSProp等)可以根据误差表面的斜率动态调整学习率。如果您想了解更多有关自适应梯度方法的信息,可以看看这篇写得很好的博文。
Python实现
如果我们根据矩阵和向量进行思考,在Python中实现多层感知机非常容易。如果输入是向量x,第一层的权重是矩阵w1,第二层的权重为矩阵w2,正向传播可以表示为x矩阵向量和w1之间的乘积,该乘积在隐藏层中生成一个名为h的激活,然后使用该向量与在第二层中的权重矩阵w2乘积后产生输出y。我会将所有内容嵌入到一个叫做MLP的类中,以后我们将会使用这个类。在这里我说明了该类的方法,你可以在GitHub存储库中找到完整的代码,并可在脚本mlp.py中找到MLP类,让我们从__init__()方法开始:
def __init__(self, tot_inputs, tot_hidden, tot_outputs):
'''Init an MLP object
Defines the matrices associated with the MLP.
@param: tot_inputs
@param: tot_hidden
@param: tot_outputs
'''
import numpy as np
if(activation!="sigmoid" and activation!="tanh"):
raise ValueError("[ERROR] The activation function "
+ str(activation) + " does not exist!")
else:
self.activation = activation
self.tot_inputs = tot_inputs
self.W1 = np.random.normal(0.0, 0.1, (tot_inputs+1, tot_hidden))
self.W2 = np.random.normal(0.0, 0.1, (tot_hidden+1, tot_outputs))
self.tot_outputs = tot_outputs你应该注意到tot_inputs+1和tot_hidden+1,就可以明白我是如何在权重矩阵增加附加行作为偏置项的。如本文和前面所述,偏置项是输入向量x和隐藏的激活h中的一个附加单元。矩阵的权重使用高斯分布随机初始化,平均值为0.0,标准差为0.1。好的,我们现在可以看一下该类的其他方法:激活函数和前向传播。
def _sigmoid(self, z):
return 1.0 / (1.0 + np.exp(-z))
def _tanh(self, z):
return np.tanh(z)
def forward(self, x):
'''Forward pass in the neural network
Forward pass via dot product
@param: x the input vector (must have shape==tot_inputs)
@return: the output of the network
'''
self.x = np.hstack([x, np.array([1.0])]) #add the bias unit
self.z1 = np.dot(self.x, self.W1)
if(self.activation=="sigmoid"):
self.h = self._sigmoid(self.z1)
elif(self.activation=="tanh"):
self.h = self._tanh(self.z1)
self.h = np.hstack([self.h, np.array([1.0])]) #add the bias unit
self.z2 = np.dot(self.h, self.W2) #shape [tot_outputs]
if(self.activation=="sigmoid"):
self.y = self._sigmoid(self.z2)
elif(self.activation=="tanh"):
self.y = self._tanh(self.z2)
return self.y有几点需要注意,我使用Numpy在方法hstack()添加了偏置单元,它同时对输入和隐藏激活函数进行了处理。我添加了两个激活函数:sigmoid和双曲正切(tanh),两者之间的区别是在于输出,sigmoid的输出范围是[0,1],而tanh的输出范围是[−1,1],您可以通过增加其他方法来扩展激活函数的功能。下面是反向传播方法:
def _sigmoid_derivative(self, z):
return self._sigmoid(z) * (1.0 - self._sigmoid(z))
def _tanh_derivative(self, z):
return 1 - np.square(np.tanh(z))
def backward(self, y, target):
'''Backward pass in the network
@param y: the output of the network in the forward pass
@param target: the value of taget vector (same shape of output)
'''
if(y.shape!=target.shape):
raise ValueError("[ERROR] The size of target is wrong!")
#gathering all the partial derivatives
dE_dy = -(target - y)
if(self.activation=="sigmoid"):
dy_dz2 = self._sigmoid_derivative(self.z2)
elif(self.activation=="tanh"):
dy_dz2 = self._tanh_derivative(self.z2)
dz2_dW2 = self.h
dz2_dh = self.W2
if(self.activation=="sigmoid"):
dh_dz1 = self._sigmoid_derivative(self.z1)
elif(self.activation=="tanh"):
dh_dz1 = self._tanh_derivative(self.z1)
dz1_dW1 = self.x
#gathering the gradient of W2
dE_dW2 = np.dot(np.expand_dims(dE_dy * dy_dz2, axis=1),
np.expand_dims(dz2_dW2, axis=0)).T
#gathering the gradient of W1
dE_dW1 = (dE_dy * dy_dz2)
dE_dW1 = np.dot(dE_dW1, dz2_dh.T)[0:-1] * dh_dz1
dE_dW1 = np.dot(np.expand_dims(dE_dW1,axis=1),
np.expand_dims(dz1_dW1,axis=0)).T
return dE_dW1, dE_dW2backward方法返回更新网络所需的梯度向量。在这里,我使用了与该帖子前面部分中使用的名称一致的偏导数的一致约定,这样就可以匹配代码和数学公式。最后,我们必须使用前向和后向传播来进行训练:
def train(self, x, target, learning_rate=0.1):
'''train the network
@param x: the input vector
@param target: the target value vector
@param learning_rate: the learning rate (default 0.01)
@return: the error RMSE
'''
y = self.forward(x)
dE_dW1, dE_dW2 = self.backward(y, target)
#update the weights
self.W2 = self.W2 - (learning_rate * dE_dW2)
self.W1 = self.W1 - (learning_rate * dE_dW1)
#estimate the error
error = 0.5 * (target - y)**2
return error这是一个基本MLP的核心代码,您可以扩展它添加更多层及误差/激活函数。请注意,当前版本的代码不包括mini-batch训练,对于这篇文章的目的,单个input-target对就足够了,但是通常随机梯度下降需要一个mini-batch的多个样本,它可以代表我们想要逼近的函数。扩展该类的方法可以加入mini-batch的训练,有两种方式可以实现:(i)第一种方法是将input-target对列表传递给train()方法,并迭代通过backward()方法累加这些对的梯度,然后在两个矩阵w1和w2上计算平均梯度;(ii)第二种方法是利用Numpy函数并实现基于张量的方法forward()和backward()。这意味着我们必须添加另一个代表mini-batch的维度,类似于Tensorflow和pyTorch等框架,可以把它作为家庭作业...
应用:多层XOR
在上一篇文章中我们看到了如何使用线性函数逼近器解决XOR问题。现在我们有了一个新的方法,多层神经网络,它是强大的非线性逼近器,能够解决XOR问题。在这里,我将使用类似于Rumelhart和al.使用的架构解决XOR问题。
在继续之前,让我们快速回顾一下。神经网络是非线性函数逼近器,与上一篇文章中介绍的线性逼近器类似,训练神经网络需要两个步骤,误差度量和更新规则:
误差度量:通过两个量之间的均方误差(MSE)给出了一个常见的误差度量。
更新规则(backprop):神经网络的更新规则基于梯度下降,并通过称为反向传播的过程获取梯度向量,反向传播是链式法则的应用。
我们可以使用神经网络来近似强化学习问题中的效用函数。我们拿清洁机器人作为例子,即在25个状态的网格世界中移动,使用标准表,我们需要把25个单元格的所有效用存储在内存中,此外,我们要访问所有25个状态来获取这些值。在这里,我们使用MLP来解决这两个问题,一个具有2个输入、2个隐藏和1个输出的MLP总共具有4 + 2 = 6个连接存储在内存中(当使用偏置时9 + 3 = 12),因此我们节省了存储空间!此外,使用MLP我们不需要访问网格世界的所有25个单元格,因为我们可以使用函数逼近以扩展到看不见的状态。
在这个例子中,我使用了一个带有2个输入,2个隐藏单元和1个输出的网络,两层中我使用tanh激活函数,这很重要,因为我们的效用函数在 [-1, +1] 范围内,而sigmoid无法逼近它。对于强化学习部分,我使用了前一篇文章的相同代码和(快速)使用matplotlib的类似绘图代码来绘制结果。您可以在GitHub存储库中找到名称为xor_mlp_td.py的完整代码,我们可以使用MLP类来定义一个新的网络并命名为my_mlp,然后训练网络来逼近效用函数。
def main():
env = init_env()
my_mlp = MLP(tot_inputs=2, tot_hidden=2, tot_outputs=1, activation="tanh")
learning_rate = 0.1
gamma = 0.9
tot_epoch = 10001
#One epoch is one episode
for epoch in range(tot_epoch):
observation = env.reset(exploring_starts=True)
#The episode starts here
for step in range(1000):
action = np.random.randint(0,4)
new_observation, reward, done = env.step(action)
#call the update method and then the my_mlp.train() method
#the update() returns the new MLP and the RMSE error
my_mlp, error = update(my_mlp, new_observation, reward,
learning_rate, gamma, done)
observation = new_observation
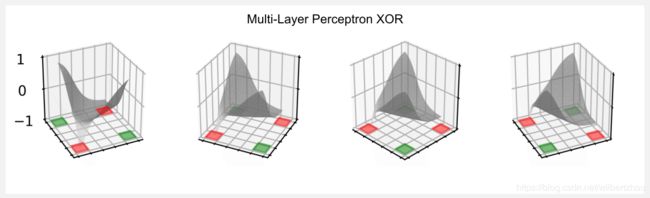
if done: break上面的代码类似于用于线性和双曲线逼近器的代码。我使用学习率0.1和γ0.9训练10000步,用x-y元组网格输入神经网络,我们可以得到近似效用函数的输出,并绘制如下图所示:
这样一个简单的神经网络可以产生一个相当复杂的函数,这与我们在前一篇文章中使用的双曲抛物面非常相似。这里打印了在上一个epoch获得的效用矩阵:
Epoch: 10001
[[ 0.81 0.23 -0.36 -0.55 -0.6 ]
[ 0.49 -0.12 -0.42 -0.49 -0.5 ]
[ 0.01 -0.18 -0.21 -0.16 -0.1 ]
[-0.44 -0.02 0.28 0.45 0.54]
[-0.87 -0.28 0.43 0.7 0.79]]在XOR世界中,矩阵的左上角和右下角具有+1的效用,而右上角和左下角具有-1的效用,我们看到网络捕获了这一趋势,其值为0.81,0.79,-0.87和-0.6。使用神经网络毫不费力地得到了这个结果,我认为对超参数进行微调可以让我们更接近。
您的家庭作业是更改网络结构,增加隐藏层的大小,并观察图是怎么变化的。请记住,增加隐藏单元的数量会增加逼近器的自由度。为了避免欠拟合和过拟合,您必须始终考虑偏差-方差的权衡。
超越多层感知机(MLP)
即使使用MLP可以在许多问题中提供很大的优势,但仍然存在一些我们未提及的主要限制,在这里,我列出其中三个:
- 模型的大小。MLP的完全连接层具有许多参数,这些参数随着单元的数量而快速增长。拥有共享权重会更好。
- 更新规则。训练具有随机梯度下降的神经网络需要独立同分布(i.i.d.)的样本,然而,从我们的网格世界收集的样本是密切相关的。
- 不稳定。在一些强化学习算法中训练神经网络可能非常不稳定(参见实例Q-learning及其bootstrap 机制)。
经过了多年时间才找到了解决所有这些问题的方案,直到最近才开发了一种稳定的算法,即深度强化学习,这将是下一篇文章的主题。
策略梯度方法
作为额外材料,我想提供一个广泛使用神经网络的另一种强化学习方法的简单概述。到目前为止,我们已经逼近了效用(或状态-动作)函数,然而,还有另一种方法:策略的逼近。在第四篇文章的最后,我解释了actor-only和critic-only算法之间的区别,策略梯度是一种actor-only的方法,目的是逼近策略。在继续学习之前,回顾效用,状态-动作和策略函数之间的区别可能很有用:
- 效用(或值)函数:y =U(s),接收向量s作为输入并返回对应状态的效用y。
- 状态-动作函数:y =Q(s, a),接收一个状态s和一个动作a作为输入,并返回对应状态-动作对的效用y。
- 策略函数:y =π(s),接收状态s作为输入并返回要在该状态下执行的动作。
在策略梯度方法中,我们使用神经网络来逼近策略函数π(s),正像名字所说的我们使用梯度。在这个系列中你应该学习到什么是梯度向量以及我们如何在梯度下降方法中使用它,在这里,我们想要估计神经网络的梯度,但我们不想再通过将误差最小化来得到,相反,我们希望最大化预期收益(长期累积奖励)。正如我之前告诉你的那样,梯度指示了最大化函数我们应该移动权重的方向,这正是我们想要在策略梯度方法中实现的。
优点:策略梯度方法的主要优点是在某些上下文中,更容易估计策略函数而不是效用函数。我们知道,由于信用分配问题,对效用函数的估计可能很困难。在策略梯度方法中,我们绕过了这个问题,我们获得了更好的收敛性和更高的稳定性;另一个优点是使用策略梯度我们可以近似连续的动作空间,这克服了Q-Learning的重要限制,其中max运算符只允许我们近似离散的动作空间(有关详细信息,请参阅第三篇文章)。
缺点:策略梯度方法的主要缺点是它们通常较慢并且通常会收敛到局部最优;另一个问题是方差,用大量轨迹评估策略会导致函数逼近中变化非常大。
最广泛使用的策略梯度方法之一称为REINFORCE,它基于蒙特卡罗方法。REINFORCE算法在不使用任何效用函数的情况下找到梯度的无偏估计。我希望有时间在将来的帖子中讲解REINFORCE,目前如果你想了解更多信息,可以阅读相关学术文章。
结论
在这篇文章中,我们学到了前馈神经网络如何工作以及它们如何用于逼近效用函数。最近的发展已经超越了MLP,使用了卷积神经网络和稳定的训练技术,最令人印象深刻的结果是在诸如ATARI游戏和古老的围棋游戏等挑战性问题中获得的。在下一篇文章中,我们将看到如何使用深度强化学习来解决其中的一些问题。
索引
- [第一篇]马尔科夫决策过程,贝尔曼方程,值迭代和策略迭代算法。
- [第二篇]蒙特卡罗概念,蒙特卡洛方法,预测与控制,广义策略迭代,Q函数。
- [第三篇]时间差分概念,动物学习,TD(0), TD(λ)和资格痕迹,SARSA,Q-learning。
- [第四篇] Actor-Critic方法背后的神经生物学,计算Actor-Critic方法,Actor-only和Critic-only方法。
- [第五篇]进化算法介绍,强化学习中的遗传算法,遗传算法的策略选择。
- [第六篇]强化学习应用,多臂老虎机,山地车,倒立摆,无人机着陆,难题。
- [第七篇]函数逼近概念,线性逼近器,应用,高阶逼近器。
- [第八篇] 非线性函数逼近,感知器,多层感知器,应用,政策梯度。
参考
Goodfellow, I., Bengio, Y., Courville, A., & Bengio, Y. (2016). Deep learning. Cambridge: MIT press.
Hebb, D. O. (2005). The first stage of perception: growth of the assembly. In The Organization of Behavior (pp. 102-120). Psychology Press.
Minsky, M., & Papert, S. A. (2017). Perceptrons: An introduction to computational geometry. MIT press.
Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. nature, 323(6088), 533.
Sutton, R. S., McAllester, D. A., Singh, S. P., & Mansour, Y. (2000). Policy gradient methods for reinforcement learning with function approximation. In Advances in neural information processing systems (pp. 1057-1063).