八大排序算法【下】 -- 归并、快排

归并排序

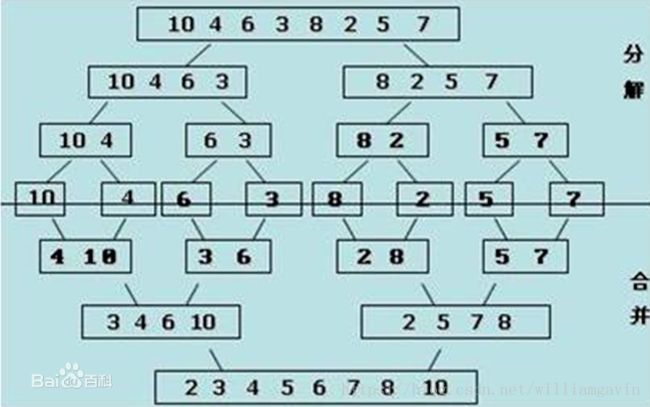
归并排序（Merge）是将两个（或两个以上）有序表合并成一个新的有序表，即把待排序序列分为若干个子序列，每个子序列是有序的。然后再把有序子序列合并为整体有序序列。

不如看图

上面的解释和图片均来自百度百科。

使用递归进行归并排序

void Merge(int SR[], int TR[], int i, int m, int n)
{
    int j, k, l;
    for (j = m+1, k = i; i <= m && j <= n; k++)
    {
        if (SR[i] < SR[j])
        {
            TR[k] = SR[i++];
        }
        else
            TR[k] = SR[j++];
    }
    if (i <= m)
    {
        for (l = 0; l <= m-i; l++)
        {
            TR[k+l] = SR[i+l];
        }
    }
    if (j <= n)
    {
        for (l = 0; l <= n-j; l++)
        {
            TR[k+l] = SR[j+l];
        }
    }
}
void MSort(int SR[], int TR1[], int s, int t)
{
    int m;
    int TR2[MAXSIZE+1];
    if (s == t)
    {
        TR1[s] = SR[s];
    }
    else
    {
        m = (s+t)/2;                // 将 SR[s..t]平分为SR[s..m]和SR[m+1..t]
        MSort(SR, TR2, s, m);       // 递归将SR[s..m]归并为有序的TR2[s..m]
        MSort(SR, TR2, m+1, t);     // 递归将SR[m+1..t]归并为有序TR2[m+1..t]
        Merge(TR2, TR1, s, m, t);   // 将TR2[s..m]和TR2[m+1..t]归并到TR1[s..t]
    }
}
// 归并排序 1
void MergeSort(SqList * L)
{
    MSort(L->r, L->r, 1, L->length);
}

上面Merge(）函数就是将两个子序列按从小到大的顺序排序成一个序列。也是归并排序的核心步骤。

归并排序的时间复杂度

归并排序的时间复杂度为O(nlogn)；最好，最坏，平均都是O(nlogn);
因为归并排序中关键字不存在跳跃，因此归并排序是一种稳定的排序方法。
但是归并排序比较占内存，因为需要与原始记录序列相同数量的存储空间存放归并结果（这点在下面的代码里面有直接的体现）以及递归时的深度为log2n的栈空间，空间复杂度为O(n+logn)。归并排序是用空间换取时间的一种排序算法。
不使用递归代码：

void MergePass(int SR[], int TR[], int s, int n)
{
    int i = 1;
    int j;
    while (i <= n-2*s+1)
    {
        Merge(SR, TR, i, i+s-1, i+2*s-1);
        i = i + 2*s;
    }
    if (i < n-s+1)
        Merge(SR, TR, i, i+s-1, n);
    else
        for (j = i; j <= n ; j++)
            TR[j] = SR[j];
}
// 归并排序 2
void MergeSort2(SqList * L)
{
    int * TR = (int *)malloc(L->length * sizeof(int ));     //分配足够大的空间
    int k = 1;
    while(k < L->length)
    {
        MergePass(L->r, TR, k, L->length);
        k = 2*k;
        MergePass(TR, L->r, k, L->length);
        k = 2*k;
    }
}

快排

快排的基本思路：在待排序列中选定一个值（称为枢轴），然后将大于枢轴的值都放在枢轴的右边（默认从小到大排序），小于枢轴的值都放在枢轴的左边；就相当于原来的序列被枢轴分成了两个子序列，然后再在这两个子序列中选定分别选定枢轴，将这两个子序列分成四个子序列…………如此往复，排序成功。
代码如下：

int Partition(SqList * L, int low, int high)
{
    int pivotkey;
    pivotkey = L->r[low];
    while (low < high)
    {
        while (lowr[high]>=pivotkey)
        {
            high --;
        }
        swap(L, low, high);         // 将比枢轴记录小的记录交换到左边
        while (lowr[low]<=pivotkey)
        {
            low ++;
        }
        swap(L, low, high);         //将比枢轴大的记录交换到右边
    }
    return low;         // low下标为pivotkey-1
}

void QSort(SqList *L, int low, int high)
{
    int pivot;
    if (low < high)
    {
        pivot = Partition(L, low, high);   // 将L->[low, high]一分为二

        QSort(L, low, pivot-1);            // 对低子序列递归排序
        QSort(L, pivot+1, high);           // 对高子序列递归排序
    }
}

// 快排
void QuickSort(SqList * L)
{
    QSort(L,1,L->length);
}

快排的时间复杂度

最优的情况下，也就是pivotkey取值非常合适的情况下，时间复杂度为 O(nlogn)；
最坏的情况下，也就是每次只得到比上次少一个记录的情况，时间复杂度为O(n^2)；平均情况下：O(nlogn)；
注意：由于快排的数据交换是跳跃式进行的，因此它是不稳定的。

快排的优化

优化枢轴

前面代码中的枢轴都是待排序列的第一个元素，这样很明显不是一种好的策略，因为如果第一个元素就是序列中最大（最小）的数，那么经过一轮的 Partition() 之后其实做的事情很少，就只是将这个枢轴放在最后面去了。比如：{9，1，4，7，3，2，8}这个序列，如果选 9 为枢轴的话，经过一轮Partition()只是将 9 和 8 换了一个位置，如果再选择 8 为枢轴，那……
枢轴最好是序列的平均数附近的值，于是有了三数取中法（median-of-three）。即先将三个关键字进行排序，将中间数作为枢轴；一般都是取最左端、最右端和中间的三个数（因为待排序列极有可能是基本有序的）。
也就是只要将Partition()函数里面的

int pivotkey;
pivotkey = L->r[low];`

改成如下形式就可以了，

int pivotkey;
int m = low + (high - low )/2;
if (L->r[low] > L->r[high])
    swap(L, low, high);
if (L->r[m] > L->r[high])
    swap(L, m, high);
if (L->r[m] > L->r[low])
    swap(L, m, high);
pivotkey = L->r[low];

三数取中对于小数组来说右很大概率可以取到一个比较好的pivotkey，但是对于大数组来说就不一定了，对于大数组可以采用 九数取中法 等方法来取到一个比较好的pivotkey。

优化小组数的排序方案

快排比较适合大数组的排序，对于一些小数组的排序可以效果还比不上其他的算法，比如：直接插入法。因此可以设置一个数组长度标志，当待排序数组大于数组长度标志时使用快排，小于时使用直接插入排序。