作者:寒小阳 时间:2013年9月。
出处:http://blog.csdn.net/han_xiaoyang/article/details/11596001。
声明:版权所有,转载请注明出处,谢谢。
0、前言
从这一部分开始直接切入我们计算机互联网笔试面试中的重头戏算法了,初始的想法是找一条主线,比如数据结构或者解题思路方法,将博主见过做过整理过的算法题逐个分析一遍(博主当年自己学算法就是用这种比较笨的刷题学的,囧),不过又想了想,算法这东西,博主自己学的过程中一直深感,基础还是非常重要的,很多难题是基础类数据结构和题目的思想综合发散而来。比如说作为最基本的排序算法就种类很多,而事实上笔试面试过程中发现掌握的程度很一般,有很多题目,包括很多算法难题,其母题或者基本思想就是基于这些经典算法的,比如说快排的partition算法,比如说归并排序中的思想,比如说桶排序中桶的思想。
这里对笔试面试最常涉及到的12种排序算法(包括插入排序、二分插入排序、希尔排序、选择排序、冒泡排序、鸡尾酒排序、快速排序、堆排序、归并排序、桶排序、计数排序和基数排序)进行了详解。每一种算法都有等板块,希望能帮助大家真正理解这些排序算法,并能使用这些算法的思想解决一些题。不多说了,下面就进入正题了。
一、插入排序
1)算法简介
插入排序(Insertion Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,。
2)算法描述和分析
一般来说,插入排序都采用in-place在数组上实现。具体算法描述如下:
如果目标是把n个元素的序列升序排列,那么采用插入排序存在最好情况和最坏情况。最好情况就是,序列已经是升序排列了,在这种情况下,需要进行的比较操作需(n-1)次即可。最坏情况就是,序列是降序排列,那么此时需要进行的比较共有n(n-1)/2次。插入排序的赋值操作是比较操作的次数减去(n-1)次。平均来说。因而,插入排序不适合对于数据量比较大的排序应用。但是,如果需要排序的数据量很小,例如,量级小于千,那么插入排序还是一个不错的选择。 插入排序在工业级库中也有着广泛的应用,在STL的sort算法和stdlib的qsort算法中,都将插入排序作为快速排序的补充,用于少量元素的排序(通常为8个或以下)。
3)算法图解、视频演示
图解:
视频:插入排序舞蹈
)
4)算法代码
void insertion_sort(int array[], int first, int last)
{
int i,j;
int temp;
for (i = first+1; i<=last;i++)
{
temp = array[i];
j=i-1;
//与已排序的数逐一比较,大于temp时,该数后移
while((j>=first) && (array[j] > temp)) //当first=0,j循环到-1时,由于[[短路求值]],不会运算array[-1]
{
array[j+1] = array[j];
j--;
}
array[j+1] = temp; //被排序数放到正确的位置
}
}
5)考察点,重点和频度分析
把插入排序放在第一个的原因是因为其出现的频度不高,尤其是这里提到的直接排序算法,基本在笔试的选择填空问时间空间复杂度的时候才可能出现。毕竟排序速度比较慢,因此算法大题中考察的次数比较比较少。
6)笔试面试例题
例题1、
请写出链表的插入排序程序
template
struct list_node
{
struct list_node *next;
T value;
};
template
struct _list
{
struct list_node *head;
int size;
};
template
void SortLink(struct _list * link) {
struct list_node *pHead,*pRear,*p,*tp;
if (!link) return;
for (pHead=link->head,pRear=0;pHead;pHead=pHead->next) {
for (tp=pHead,p=pHead->next;p;tp=p,p=p->next)
if (pHead->value>=p->value)
tp->next=p->next,p->next=pHead,pHead=p,p=tp;
if (!pRear) link->head=pHead;
else pRear->next=pHead;
pRear=pHead;
}
}
例题2、
A.快速排序 B.冒泡排序 C.直接插入排序
二、二分插入排序
1)算法简介
二分(折半)插入(Binary insert sort)排序是一种在直接插入排序算法上进行小改动的排序算法。其与直接排序算法最大的区别在于,在速度上有一定提升。
2)算法描述和分析
一般来说,插入排序都采用in-place在数组上实现。具体算法描述如下:
1)稳定
2)空间代价:O(1)
3)时间代价:插入每个记录需要O(log i)比较,最多移动i+1次,最少2次。最佳情况O(n log n),最差和平均情况O(n^2)。
二分插入排序是一种稳定的排序。,。二分插入排序元素移动次数与直接插入排序相同,依赖于元素初始序列。
3)算法图解、视频演示
图解:
视频:二分插入排序
4)算法代码
void BinInsertSort(int a[], int n)
{
int key, left, right, middle;
for (int i=1; ikey)
right = middle-1;
else
left = middle+1;
}
for(int j=i-1; j>=left; j--)
{
a[j+1] = a[j];
}
a[left] = key;
}
}
5)考察点,重点和频度分析
这个排序算法在笔试面试中出现的频度也不高,但毕竟是直接排序算法的一个小改进算法,同时二分查找又是很好的思想,有可能会在面试的时候提到,算法不难,留心一下就会了。
6)笔试面试例题
例题1、
A、二分插入排序 C、冒泡排序 D、快速排序
例题2、
(1)冒泡排序;(2)选择排序;(3)插入排序;(4)二分插入排序;(5)快速排序;(6)堆排序;(7)归并排序;
三、希尔排序
1)算法简介
希尔排序,也称递减增量排序算法,因DL.Shell于1959年提出而得名,是插入排序的一种高速而稳定的改进版本。
2)算法描述
希尔排序的时间复杂度与增量序列的选取有关,例如希尔增量时间复杂度为O(n2),而Hibbard增量的希尔排序的时间复杂度为O(N(5/4)),但是现今仍然没有人能找出希尔排序的精确下界。
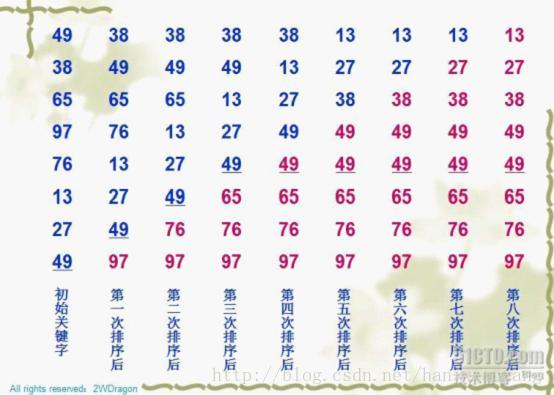
3)算法图解、视频演示
图解:
视频:希尔排序Shell Sort 舞蹈
4)算法代码
#include
int main()
{
const int n = 5;
int i, j, temp;
int gap = 0;
int a[] = {5, 4, 3, 2, 1};
while (gap<=n)
{
gap = gap * 3 + 1;
}
while (gap > 0)
{
for ( i = gap; i < n; i++ )
{
j = i - gap;
temp = a[i];
while (( j >= 0 ) && ( a[j] > temp ))
{
a[j + gap] = a[j];
j = j - gap;
}
a[j + gap] = temp;
}
gap = ( gap - 1 ) / 3;
}
}
5)考察点,重点和频度分析
事实上希尔排序算法在笔试面试中出现的频度也不比直接插入排序高,但它的时间复杂度并不是一个定值,所以偶尔会被面试官问到选择的步长和时间复杂度的关系,要稍微有点了解吧。算法大题中使用该方法或者其思想的题也不多。
6)笔试面试例题
例题1、
程序略,需要O(n^2)次的比较
例题2、
,则:
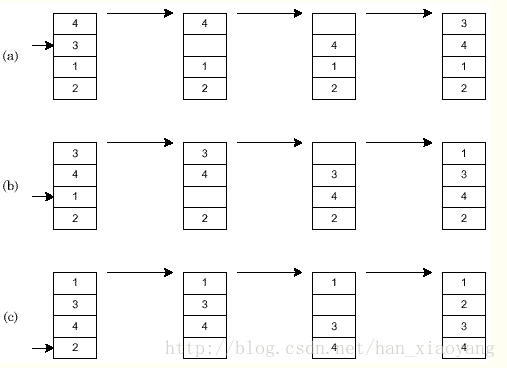
冒泡排序一趟扫描的结果是 ;
初始步长为4的希尔(shell)排序一趟的结果是 ;
二路归并排序一趟扫描的结果是 ;
快速排序一趟扫描的结果是 ;
堆排序初始建堆的结果是 。
四、选择排序
1)算法简介
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理如下。,。以此类推,直到所有元素均排序完毕。
2)算法描述和分析
n个记录的文件的直接选择排序可经过n-1趟直接选择排序得到有序结果:
。,。
选择排序的交换操作介于0和(n-1)次之间。选择排序的比较操作为n(n-1)/2次之间。选择排序的赋值操作介于0和3(n-1)次之间。比较次数O(n^2),比较次数与关键字的初始状态无关,总的比较次数N=(n-1)+(n-2)+...+1=n*(n-1)/2。 交换次数O(n),最好情况是,已经有序,交换0次;最坏情况是,逆序,交换n-1次。 交换次数比冒泡排序少多了,由于交换所需CPU时间比比较所需的CPU时间多,n值较小时,选择排序比冒泡排序快。
| 最差时间复杂度 | О(n²) |
| 最优时间复杂度 | О(n²) |
| 平均时间复杂度 | О(n²) |
| 最差空间复杂度 | О(n) total, O(1) |
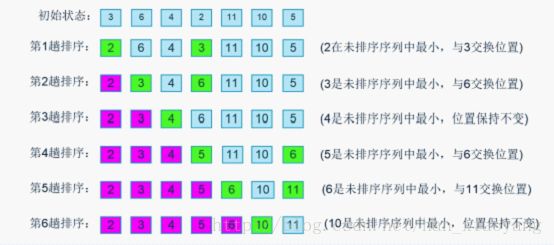
3)算法图解、视频演示
图解:
视频:选择排序Select Sort排序舞蹈
4)算法代码
void selection_sort(int *a, int len)
{
register int i, j, min, t;
for(i = 0; i < len - 1; i ++)
{
min = i;
//查找最小值
for(j = i + 1; j < len; j ++)
if(a[min] > a[j])
min = j;
//交换
if(min != i)
{
t = a[min];
a[min] = a[i];
a[i] = t;
}
}
}
5)考察点,重点和频度分析
就博主看过的笔试面试题而言,选择算法也大多出现在选择填空中,要熟悉其时间和空间复杂度,最好最坏的情况分别是什么,以及在那种情况下,每一轮的比较次数等。
6)笔试面试例题
例题1、
:(到尾部) ;: 。
例题2、
A. 插入排序 C. 归并排序 D. 选择排序
五、冒泡排序
1)算法简介
冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
2)算法描述
冒泡排序是与插入排序拥有相等的执行时间,但是两种法在需要的交换次数却很大地不同。在最坏的情况,冒泡排序需要O(n2)次交换,而插入排序只要最多O(n)交换。冒泡排序的实现(类似下面)通常会对已经排序好的数列拙劣地执行(O(n2)),而插入排序在这个例子只需要O(n)个运算。因此很多现代的算法教科书避免使用冒泡排序,而用插入排序取代之。冒泡排序如果能在内部循环第一次执行时,使用一个旗标来表示有无需要交换的可能,也有可能把最好的复杂度降低到O(n)。在这个情况,在已经排序好的数列就无交换的需要。若在每次走访数列时,把走访顺序和比较大小反过来,也可以稍微地改进效率。有时候称为往返排序,因为算法会从数列的一端到另一端之间穿梭往返。
| 最差时间复杂度 | O(n^2) |
| 最优时间复杂度 | O(n) |
| 平均时间复杂度 | O(n^2) |
| 最差空间复杂度 | 总共O(n),需要辅助空间O(1) |
3)算法图解、视频演示
图解:
视频:舞动的排序算法 冒泡排序
4)算法代码
#include
void bubbleSort(int arr[], int count)
{
int i = count, j;
int temp;
while(i > 0)
{
for(j = 0; j < i - 1; j++)
{
if(arr[j] > arr[j + 1])
{ temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
i--;
}
}
int main()
{
//测试数据
int arr[] = {5, 4, 1, 3, 6};
//冒泡排序
bubbleSort(arr, 5);
//打印排序结果
int i;
for(i = 0; i < 5; i++)
printf("%4d", arr[i]);
}
5)考察点,重点和频度分析
一般我们学到的第一个排序算法就是冒泡排序,不得不说,这个还真是一个很常见的考点,平均时间空间复杂度,最好最坏情况下的时间空间复杂度,在不同情况下每一趟的比较次数,以及加标志位减少比较次数等,都是需要注意的地方。
6)笔试面试例题
例题1、
例题2、
事实上,这道题放到冒泡排序这里不知道是不是特别合适,只是有一种解法是类似冒泡的思想,如下解法一
每次遇到大写字母就往后冒,最后结果即为所求
#include
#include
//题目以及要求:把一个字符串的大写字母放到字符串的后面,
//各个字符的相对位置不变,不能申请额外的空间。
//判断是不是大写字母
int isUpperAlpha(char c){
if(c >= 'A' && c <= 'Z'){
return 1;
}
return 0;
}
//交换两个字母
void swap(char *a, char *b){
char temp = *a;
*a = *b;
*b = temp;
}
char * mySort(char *arr, int len){
if(arr == NULL || len <= 0){
return NULL;
}
int i = 0, j = 0, k = 0;
for(i = 0; i < len; i++){
for(j = len - 1 - i; j >= 0; j--){
if(isUpperAlpha(arr[j])){
for(k = j; k < len - i - 1; k++){
swap(&arr[k], &arr[k + 1]);
}
break;
}
//遍历完了字符数组,但是没发现大写字母,所以没必要再遍历下去
if(j == 0 && !isUpperAlpha(arr[j])){
//结束;
return arr;
}
}
}
//over:
return arr;
}
int main(){
char arr[] = "aaaaaaaaaaaaaaaaaaaaaaaAbcAdeBbDc";
printf("%s\n", mySort(arr, strlen(arr)));
return 0;
}
。
步骤如下
1、两个指针p1和p2,从后往前扫描
2、p1遇到一个小写字母时停下, p2遇到大写字母时停下,两者所指向的char交换
3、p1, p2同时往前一格
代码如下:
#include
#include
//判断是不是大写字母
int isUpperAlpha(char c){
if(c >= 'A' && c <= 'Z'){
return 1;
}
return 0;
}
//交换两个字母
void swap(char *a, char *b){
char temp = *a;
*a = *b;
*b = temp;
}
char * Reorder(char *arr, int len){
if(arr == NULL || len <= 0){
return NULL;
}
int *p1 = arr;
int *p2 = arr;
While(p1 六、鸡尾酒排序/双向冒泡排序
1)算法简介
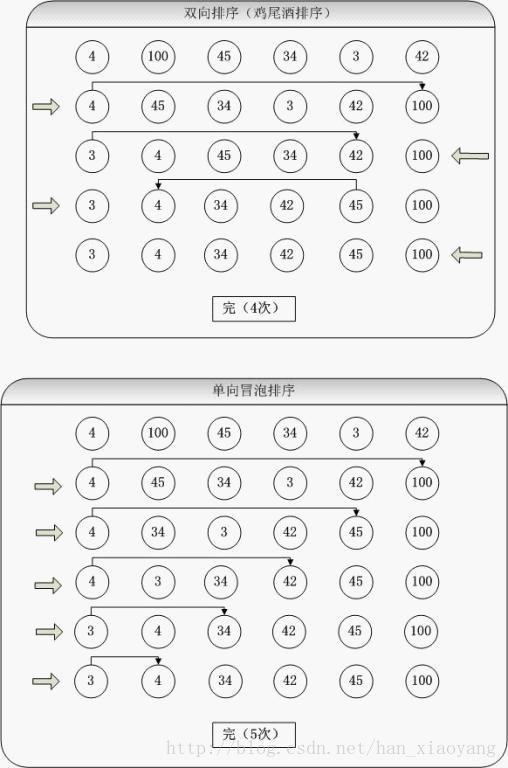
鸡尾酒排序等于是冒泡排序的轻微变形。不同的地方在于,而冒泡排序则仅从低到高去比较序列里的每个元素。他可以得到比冒泡排序稍微好一点的效能,原因是冒泡排序只从一个方向进行比对(由低到高),每次循环只移动一个项目。
2)算法描述和分析
;
。
。
。
鸡尾酒排序最糟或是平均所花费的次数都是O(n^2),但如果序列在一开始已经大部分排序过的话,会接近O(n)。
| 最差时间复杂度 | O(n^2) |
| 最优时间复杂度 | O(n) |
| 平均时间复杂度 | O(n^2) |
3)算法图解、视频演示
图解:
4)算法代码
void CocktailSort(int *a,int nsize)
{
int tail=nsize-1;
for (int i=0;ii;--j) //第一轮,先将最小的数据排到前面
{
if (a[j]a[j+1])
{
int temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
tail--; //原tail处数据也已排好序,将其减1
}
}
5)考察点,重点和频度分析
鸡尾酒排序在博主印象中出现的频度也不高,用到它的算法题大题很少,选择填空出现的话多以双向冒泡排序的名称出现,注意注意时间空间复杂度,理解理解算法应该问题就不大了。
6)笔试面试例题
考点基本类似冒泡排序,请参考上一节