吴恩达深度学习第一课第三周(浅层神经网络)

打卡（1）

3.1 神经网络概览

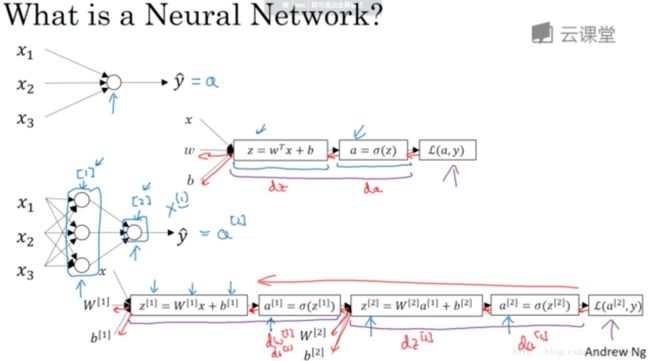
* 可以很多个sigmoid单元堆叠起来构成一个神经网络。
* 图中[1]、[2]表示层((1),(2)表示单个样本)；
* 图中圆圈是sigmoid函数，由两步算的，第一步算z。第二步算a；

打卡（2）

3.2 神经网络表示

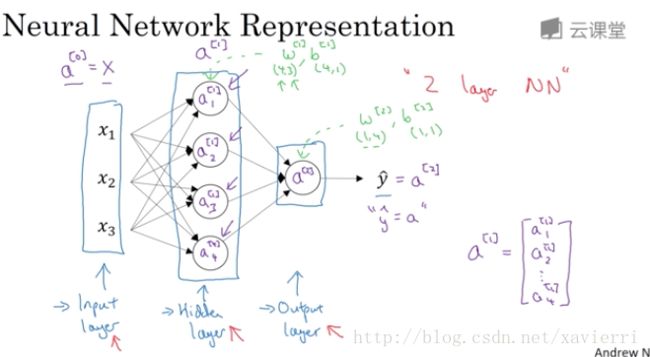
* 输入层———隐藏层————输出层————预测值（输入层一般不看作是一个标准层，神经网络的层数指隐藏层和输出层）
* 隐藏层的含义：在训练集中 这些中间节点的真正数值，是不被知道的
* 图中是一个双层神经网络

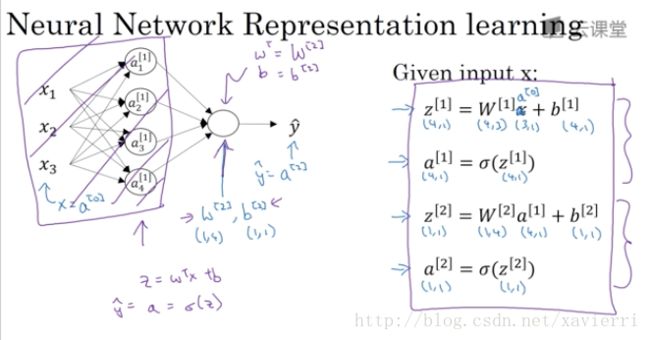
3.3. 计算神经网络的输出

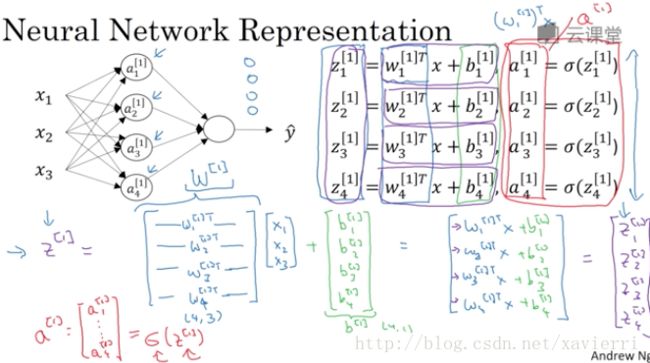
* α[θ]i α i [ θ ] 中， θ θ 值所在层， i i 表示第 θ θ 层的 i i 个节点.
* 节点进行的运算：
Z[θ]i=w[θ]TiX+b[θ]i Z i [ θ ] = w i [ θ ] T X + b i [ θ ] ;
a[θ]i=σ(Z[θ]i) a i [ θ ] = σ ( Z i [ θ ] ) ;
w[θ] w [ θ ] 和 X X 都是维度等于特征数的（列）向量.
W[θ] W [ θ ] 表示第 θ θ 层各节点参数向量转置（行向量）构成的参数矩阵

3.4 多个例子中的向量化

* α[θ]i α [ θ ] i 表示第 θ θ 第 i i 个样本 θ θ 层的激活函数 。

A[θ] A [ θ ] 矩阵中从左到右表示所有样本的第 θ θ 层激活函数向量，从上到下表示各隐藏单元（节点）第 θ θ 层激活函数向量，比如矩阵左上角的第一个点表示第一个训练样本，第 θ θ 层第一个隐藏单元的激活函数。

打卡（3）

3.5 向量化实现的解释

3.6 激活函数

* 激活函数可以是非线性函数，不一定要是sigmoid函数；
* tanh函数的阈值介于-1和1之间；
* tanh=ez−e(−z)ez+e(−z) t a n h = e z − e ( − z ) e z + e ( − z ) ；
* tanh函数上实际是sigmoid函数平移后的版本；
* 对于隐藏单元，tanh函数几乎总比sigmoid函数好，因为tanh函数可以使激活函数值得平均值趋于零，有类似数据中心化的效果，这让下一层学习更方便，目前几乎不使用sigmoid函数，tanh函数几乎在所有场合比其更优越（一个例外是二元分类）；
* 神经网络不同层的激活函数可以不一样；
* sigmoidh和tanh函数的缺点，他们在Z值很大或很小时，导数的梯度，或者说函数的斜率很小，接近0，会拖慢梯度下降算法；
* Relu函数（修正线性单元，目前最流行的激活函数）： α=max(0,Z) α = m a x ( 0 , Z ) ,只要Z为整数，函数斜率为1，为负时斜率为0，Relu的一个缺点是，Z为负数时，激活函数值为0，Relu函数的好处在于，对于很多Z空间，激活函数的斜率和0差很远，所以在实践中使用Relu函数的神经网络学习速度通常更快，虽然对于一班的Z,Relu斜率为0，但在实践中，有足够多的隐藏单元，为正，斜率不为0。

3.7 为什么需要非线性激活函数

• 如果全部使用线性激活函数，那么不管神经网络有多少层，在做的运算都是线性运算，隐藏层就不起作用
• 只有一个场景可以使用线性激活函数，就是如果你要机器学习的是回归问题。

3.8 激活函数的导数

• sigmoid函数的导数：
  
• tanh函数的导数
  
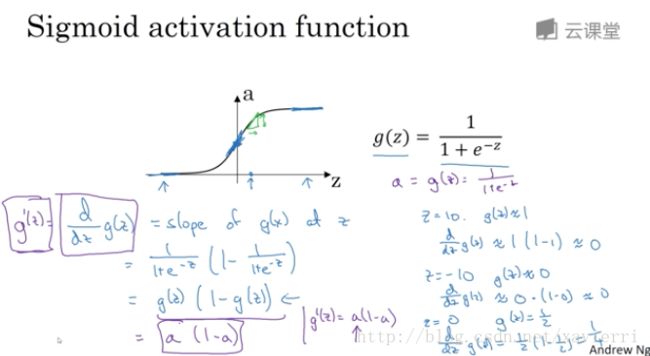
• ReLu函数和泄露ReLu函数的导数
  

3.9 神经网络的梯度下降

假设有一个单隐藏层神经网络（双层神经网络）
* nx=n[0]表示输入层的特征维度,n[1]表示隐藏层隐藏单元数据，n[2]=1是一个输出单元 n x = n [ 0 ] 表 示 输 入 层 的 特 征 维 度 , n [ 1 ] 表 示 隐 藏 层 隐 藏 单 元 数 据 ， n [ 2 ] = 1 是 一 个 输 出 单 元
* W[1]的维度是（n[1],n[0]）,W[2]的维度是（n[2]，n[1]） W [ 1 ] 的 维 度 是 （ n [ 1 ] , n [ 0 ] ） , W [ 2 ] 的 维 度 是 （ n [ 2 ] ， n [ 1 ] ）

向量化计算：
* 反向传播

db[2]=1mnp.sum(dZ[2],axis=1,keepdim=True) d b [ 2 ] = 1 m n p . s u m ( d Z [ 2 ] , a x i s = 1 , k e e p d i m = T r u e ) , keepdim=True是为了确保python输出的矩阵，且维度为（ n[2] n [ 2 ] ,1）
* 其中 dZ[1] d Z [ 1 ] 推导如下:
"dZ[1]"=dA[2]dZ[2]∗dZ[2]dA[1]∗dA[1]dZ[1]="dZ[2]"∗W[2]∗g[1]′(Z[1]) " d Z [ 1 ] "= d A [ 2 ] d Z [ 2 ] ∗ d Z [ 2 ] d A [ 1 ] ∗ d A [ 1 ] d Z [ 1 ] =" d Z [ 2 ] " ∗ W [ 2 ] ∗ g [ 1 ] ′ ( Z [ 1 ] )

3.10 直观理解反向传播

（略）

3.11 随机初始化

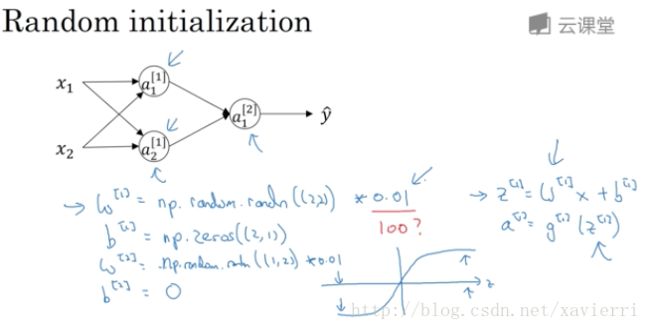
* 对于logistic回归，可以将权重 w w 初始化为0，但如果将神经网络的各参数数组全部初始化为0，再使用梯度下降，会使神经网络完全无效，因为这种情况下，隐藏层的所有节点（隐藏单元）就完全一样，那么多个隐藏单元就是去了意义
* 随机初始化所有参数:

W=np.random.randn((n, m))*0.01
b=np.zero(n,1)

• 通常把权重初始化为很小的值，因为如果权重过大，可能是Z一开始就落在是的激活函数tanh和sigmoid接近饱和的区域，从而减慢了学习速度