深度增强学习（DRL）漫谈 - 从DQN到AlphaGo

本篇博客转载自：http://blog.csdn.net/jinzhuojun/article/details/52752561

深度增强学习（Deep reinforcement learning, DRL）是DeepMind（后被谷歌收购）近几年来重点研究且发扬光大的机器学习算法框架。两篇Nature上的奠基性论文（DQN和AlphaGo）使得DRL这一深度学习（Deep learning, DL）和增强学习（Reinforcement learning, RL）的交叉方向变得炙手可热。再加上多个影响较大的benchmark（Atari 2600，围棋等）上漂亮的成绩使它如今倍受学术界和商业界的关注，甚至让人闻到了泡沫的味道。不管怎样，它还是非常成功地开创了新的方向，既具有极大学术价值也具有颇高的商业价值。尽管之后用于解决像围棋这样的大规模搜索问题，但DQN出现之初的最大意义在于算法的通用性。因为泛化性向来是机器学习最大的挑战之一，它才是机器和人相比弱太多的地方，也是很多机器学习算法最有待改进的地方。今天我们看各种小报上对人工智能研究成果的报道都喜欢断章取义，拿特定数据集上的准确性说事，虽然那也很牛X，但一定程度上忽略了通用性也是机器学习走向大众最大瓶颈之一的事实。

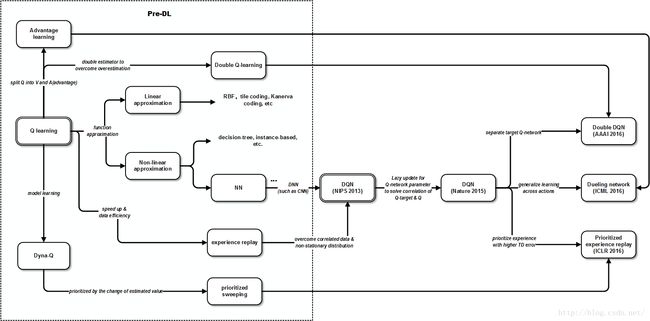
今天我们就抱着“知其然知其所以然”的态度，看看它的演变历程。其实DQN并不是一蹴而就，它是基于一个古老的人工智能方向，即增强学习。增强学习不同与机器学习中其它两大类学习方法-监督学习（supervised learning, SL）和非监督学习（unsupervised learning, UL），其基本思想是借鉴人类学习的过程，让agent（智能体，或称学习体）通过不断试错来找寻最优策略，而我们只需要设置回报（奖励和惩罚）即可。但由于其局限性（比如强依赖于人工设计的特征质量等），长期处于不温不火的境地，直到DQN使它老树发新芽，重获新生。NIPS 2013论文《Playing Atari with Deep Reinforcement Learning》提出的深度Q学习（Deep Q-learning，DQN）是基于增强学习中的Q学习（Q-learning）。那我们就以它为切入点，来看一下Q-learning是怎么来的。Sutton的经典著作《Reinforcement Learning: An Introduction》中对常规的增强学习方法做了非常好的总结。我们就参考它粗糙地勾勒下Q-learning在其中的大体位置。

从图中可以看到，增强学习发展了几十年，已经开枝散叶，有了很多分支。1989年由Watkins提出的Q学习是一种model-free（不用学习环境模型）的基于off-policy（学习过程中执行的策略与值估计使用的策略不一样）的temporal difference（TD）方法，也是RL中流传最为广泛的一种学习方法。

接下来话锋一转就需要讲函数逼近（Function approximation，FA）了。因为最原始的表格法（tabular method）来表示目标函数（V或Q函数）毕竟用途有限，且多用于离散空间。而函数逼近相比之下可有不少好处：比如一可以降低输入维度，减少计算量；二可以提高泛化能力，避免过学习（over-fitting）；三可以使目标函数对于参数可微，用上基于梯度的计算方法。前面提到RL的局限之一就是需要人工设计的特征。设计的不好后面的算法再好也白搭。这其实不只针对RL，以前我们看到分类或回归问题结果不好，就去换其它算法或改进算法本身。后来发现只要特征选取合适或设计合理，很多时候算法的结果都没有显著差异。其实深度学习本身也正是把更多注意力拉回到特征学习上来。回到正题，函数逼近分为两大类：线性和非线性的。前者一般是用一系列特征的线性组合，它们的权重作为参数。优点自然是计算方便，算法好实现。后者就比如用神经网络（Neural network，NN），优点是表达能力大大加强，缺点是训练起来也麻烦得多。当然，用NN来逼近目标函数（比如值函数）早已被人研究过，毕竟上世纪80年代的时候神经网络也如同今天的深度学习一样香饽饽。比如上世纪的TD-Gammon，可以说是当时RL在博弈应用的经典，就是用了多层神经网络作为函数逼近。但深度学习前的神经网络功能上只用于分类或回归，没有无监督学习提取特征的功能，因此难以直接处理裸数据，比如像素级数据（raw pixels）。

NIPS 2013 《Playing Atari with Deep Reinforcement Learning》

到这里为止，还没有深度学习半毛钱关系，很多都是二，三十年前的东西。作下简单的铺垫后，接下来我们看下DL是怎么让这些经典方法换发青春的。DQN中的输入采用的是原始图像数据，可以说基本是裸数据了。这是DQN最有意义的一步了。在DNN前喂裸数据一般效果都不怎么理想，因为一般的ANN无法通过自动训练catch到其中的隐含特征。而这几年涌现的一些成果，比如论文《Imagenet classification with deep convolutional neural networks》等，极大地增强了DL处理raw pixels数据的信心。说实话，纯拼Atari成绩的话，任何一个游戏都可以通过针对性的算法取得非常高的成绩，但DQN能发表在Nature上，了不起在它的算法对所有游戏是通用的（甚至超参数也是通用的），而这种通用性的重要基础之一就是它能吃raw pixels。当然它的意义不止于此，它实现了很好的效果向全世界证明了该方法的有效性，而其中的一大功臣就是experience replay。该方法在Long-Ji Lin 1993年的毕业论文中有较详细的介绍，其主要作用是克服经验数据的相关性（correlated data）和非平稳分布（non-stationary distribution）问题。它的做法是从以往的状态转移（经验）中随机采样进行训练。这样至少有两个好处：1. 数据利用率高，因为一个样本被多次使用。2. 连续样本的相关性会使参数更新的方差（variance）比较大，该机制可减少这种相关性。注意这里用的是随机采样，这也给之后的改进埋下了伏笔。

Nature 2015《Human-level control through deep reinforcement learning》

以上是NIPS 2013论文中提出的DQN原型。之后Nature 2015的论文《Human-level control through deep reinforcement learning》对之作了改进和完善。其中对于算法上的变化最主要是引入了单独的Q函数网络。研究者在实践中发现当使用如NN这样的非线性函数逼近器逼近Q函数时RL学习过程并不稳定。这种不稳定有几种原因：经验数据（即观察序列）具有相关性。Q函数的微小改变会引起策略（policy）的巨大改变，进而改变训练数据分布，以及Q函数与Q函数目标之间的差值。前者可以用experience replay解决（参见NIPS 2013论文）。后者可采用迭代式更新（iterative update）解决（Nature 2015引入）。 该方法即Q函数的参数只在一定步数后才更新，相当于延迟更新来减少Q函数和Q函数目标间的相关性。直观上，整个训练学习过程其实就是Q函数向Q函数目标逼近的过程，试想下，如果目标也跟着学习体一起变，那势必对收敛性造成影响。

到这里为止，在Q学习的基础上，DQN的大致演进路线如下。

之后，DeepMind的大牛们一刻不停地在AAAI，ICML等顶级会议中相继对DQN作了改进，使其成绩与性能有了质的飞跃。按时间顺序主要有下面论文：

AAAI 2016 《Deep Reinforcement Learning with Double Q-learning》

研究者发现，Q学习中的overestimation问题（在确定状态下Q值估计偏高）可能导致非最优解和学习过程稳定性下降。最初Thrun & Schwartz开始探讨该问题，证明了在使用函数逼近器时overestimation可能导致非最优解。之后van Hasselt发现即使用表格表示法的情况下，环境中的噪声也能导致overestimation，并且提出了解决方案Double Q-learning。而DQN是基于Q-learning，所以本质上也有这个问题。因此将Double Q-learning结合进DQN可以改善。其基本思想是将选择和评估动作分离，让它们使用不同的Q函数（网络）。其中一个用于产生贪婪策略（greedy policy），另一个用于产生Q函数估计值。实现时会有两个Q函数网络：原DQN中的Q函数网络称为在线网络（online network），后者称为目标网络（target network）。由于Nature版DQN已经引入了单独的Q目标网络，所以Double DQN对DQN架构基本不需什么改动，只需把目标网络的参数和在线网络的参数独立训练即可。注意和本文方法相比，Nature 2015上的方法相当于是参数的延迟更新，在同一步更新的动作选取和函数估计中还是用的同一个参数。

ICLR 2016《Prioritized Experience Replay》

在RL与DL结合的实践中起到比较关键作用的experience replay算法灵感可以说部分来自生物学，它类似于大脑中海马体在我们休息的时候将近期的经验回放加深印象的机制。最原始的RL是每次观察到一次状态转移（表示为s, a, R, γ, S’）只更新一次参数。这样一来有几个问题：1. 参数更新具有时间上的相关性，这与随机梯度下降算法的假设不符。2. 那些出现次数少的状态转移（经验）很快就会被“遗忘”掉。DQN中使用了experience replay来缓解这两个问题。该方法不仅稳定了函数训练过程，也提高了经验数据的利用率。缺点是需要更多内存来存储经验池（experience pool）。 这种方法的效果很好，但目前的做法还是对以往经验均匀采样的。下一步自然是根据经验的重要程度进行有侧重的replay。

在RL领域，上个世纪90年代就有类似的想法，即prioritized sweeping，应用在model-based的规划问题中。直觉上，我们知道一部分经验比其它经验要对参数的训练产生更大的作用 。基于此，该方法的基本思想是使参数更新倾向于使值估计变化更大的经验。而怎么衡量哪些经验对值估计的贡献呢，这就需要有定量的测度。在model-free的场景中，这个测度一般选用TD error。具体地，TD error越大，也就是expected learning progress越高的经验数据，可以让它们replay的次数越频繁。基于这种思想实现的greedy TD-error prioritization算法将经验数据和其TD error按序存在replay memory中，每次取最大TD error的经验进行replay，同时参数更新的量也与之同比。另外新的经验会设成最大优先级以保证它至少被训练一次。

论文还提到这种做法会导致loss of diversity问题和引入bias，但文中分别用stochastic prioritization和importance sampling方法来减轻和纠正。总得来说，按文的原话说，experience replay使得参数的更新不再受限于实际经验的顺序，prioritized experience replay继而使之不再受限于实际经验的出现频率。

ICML 2016《Dueling Network Architectures for Deep Reinforcement》

这篇论文提出了针对model-free RL的dueling network框架。它是对传统DQN架构层面上的改动，将基于状态的V函数（value function）和状态相关的advantage函数（advantage function）分离。Advantage函数的思想基于1993年Baird提出的advantage updating。除了传统的V函数外，引入的advantage函数 A(x, u)的定义是当采取动作u相比于采取当前最优动作能多带来多少累积折扣回报。简单粗暴得说，就是选这个动作比当前最优动作（或其它动作）好多少。

基于这个思想，同一个网络会同时估计V函数和advantage函数，它们结合起来可以得到Q函数。从架构上来说，这是一个一分为二，再合二为一的过程。它的出发点是因为对于很多状态，其实并不需要估计每个动作的值。可以预见到，引入advantage函数后，对于新加入的动作可以很快学习，因为它们可以基于现有的V函数来学习。它直觉上的意义在于将Q函数的估计分为两步。这样，可以先估计哪些状态更能获得更多回报，而不受该状态下不同动作的干扰。文中举了典型的赛车游戏的例子。可以看到V函数专注于远处（地平线）和分数，也就是长期目标，advantage函数专注于附近障碍，也就是短期目标。这说明V函数和advantage函数分别学习到了两个层次的策略。这种分层学习的做法有几个好处：一是V函数可以得到更多的学习机会，因为以往一次只更新一个动作对应的Q函数。二是V函数的泛化性更好，当动作越多时优势越明显。直观上看，当有新动作加入时，它并不需要从零开始学习。三是因为Q函数在动作和状态维度上的绝对数值往往差很多，这会引起噪声和贪婪策略的突变，而用该方法可以改善这个问题。

将这些改进考虑进去，我们可以把上面的图再延伸出去：

Nature 2016 《Mastering the game of Go with deep neural networks and tree search》

DRL的第二波高潮当属Nature 2016 上的论文《Mastering the Game of Go with Deep Neural Networks and Tree Search》，其中发表了AlphaGo的相关成果。它应用了DRL技术将围棋智能水平达到了一个全新的高度。我们都知道在这类信息完全博弈游戏中人工智能迟早会战胜人（因为在类似于启发式搜索问题上，人的智能会受到大脑开发的生理极限限制，而计算能力的发展可以以数量级速度增长，再加上有合适的方法出现就可以使其搜索效率极大提高），但AlphaGo似乎让它提前了好多年实现。AlphaGo虽然也基于DRL，但其意义与之前基于DQN的工作大相径庭，否则《Nature》也不会让它发两次。如果说之前的最开始提出的DQN还是一种算法的话，AlphaGo这时就已经是一套为围棋精心设计的算法框架了。前面提到过，DQN的意义在于算法具有通用性，而AlphaGo的意义在于围棋问题本身的搜索空间非常之大，同时也是经典的NP-hard问题。AlphaGo通过蒙特卡洛搜索树（Monte-Carlo Tree Search，MCTS）和DRL结合使得这个大规模搜索问题在可计算范围内。它没有用raw pixels作输入（也无必要），而是使用人工设计的特征用于policy network和value network的训练。其实AlphaGo更多是个工程上的杰作。它基于前面的DRL基础上，做了很多针对围棋问题的特有技术，且用了分布式的技术加速计算。总之，它们要展示的是DRL两方面的能力，DQN是算法的通用能力，AlphaGo是对于变态级规模搜索问题的计算有效性。

AlphaGo的大体思想是使用value network来评估棋盘位置，用policy network来选择动作，同时结合了监督学习和DRL技术。它还引入了一种结合MC模拟和value/policy network的搜索算法。

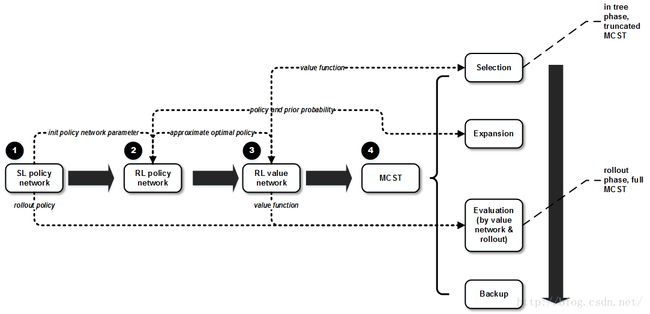
架构上，value network用于评估位置，policy network用于采样动作。流程上，学习分为几个阶段：第一阶段基于人类专家的数据集通过监督学习训练SL policy network。另外训练一个单独的策略用于在之后的rollout中快速选取动作。这一步更多是为了结合人类已有经验（毕竟纯靠自学习有些慢），用于后面几步作先验知识。接着，将SL policy network的参数来初始化RL policy network （该policy network用于之后在RL中通过self-play做策略搜索）。第二阶段是通过RL的policy gradient方法学习策略，通过随机梯度上升（Stochastic gradient ascent）算法来更新RL policy network参数。第三阶段，学习value network用于预测RL policy network玩游戏时的胜算，这一步使用随机梯度下降（Stochastic gradient descent，SGD）来最小化outcome（对当前状态而言围棋结束时的回报，即输赢）与V函数之间的差（用MSE表示）。最后，第四阶段中，有了上面的policy network和value network，就可以据此用MCST来进行搜索了。

在最后一个阶段中，算法会通过MC模拟从根状态来往下单向遍历搜索树，这一阶段又可以分为选取（selection），扩展（expansion），评估（evaluation）和回溯（backup）四步。这其实也是MCST算法框架中的经典的四个步骤。只是AlphaGo在这个MCTS算法中结合了policy和value network。其中选取这步基于前面的value network取Q函数值最大的动作。注意这一步使用的是UCT族算法，它在动作选取时除Q函数值还会考虑一个代表未知程度的量，用于解决著名的exploration-exploitation问题。毕竟，我们的期望是程序不仅仅是复制人类的经验，而且能够超越。第二步扩展是针对搜索树中的叶子结点，使用的是RL policy network中学习到的策略。第三步评估有两种完全不同的方式：1. 通过value network。2.通过随机rollout直到结束（使用fast rollout policy，也就是之前的SL policy network）所得到的回报。这两者可通过参数进行调和。最后回溯这步即根据前面的搜索进行Q函数更新。

总得来说可以大体概括为下图：

可以看到，今天的的人工智能和机器学习领域，工程和学术同样重要。一方面可能因为DL的特殊性，毕竟它基于的神经网络从一开始就是偏工程的；另一方面今天的工业与学术结合更加紧密，产业化速度大大加快。比如DRL的idea很好，但前提是要有工程能力证明它好。即使有人早几年想到了这个idea，它仍不一定能使它发在Nature这样的高级别刊物上。因为今天的DRL是工程和学术的充分结合。另外，这还提醒我们要重视学科或者说是方向的交叉。很多时候，一篇论文的学术价值取决于它能给后人留多少可以继续深究的东西。除了那些能自成一派的极端牛人，大多数时候能连接两个或多个方向并证明其价值所带来的影响就非常深远了。