字符串多模式匹配：AC算法

　　早在1975年贝尔实验室的两位研究人员Alfred V. Aho 和Margaret J. Corasick就提出了以他们的名字命名的高效的匹配算法—AC算法。该算法几乎与《KMP算法》同时问世。与KMP算法相同，AC算法时至今日仍然在模式匹配领域被广泛应用。
　　
　　AC算法是一个经典的多模式匹配算法，可以保证对于给定的长度为n的文本，和模式集合P{p1,p2,…pm}，在O(n)时间复杂度内，找到文本中的所有目标模式，而与模式集合的规模m无关。
　　
　　正如KMP算法在单模式匹配方面的突出贡献一样，AC算法对于多模式匹配算法后续的发展也产生了深远的影响，而且更为重要的是，两者都是在对同一问题——模式串前缀的自包含问题的研究中，产生出来的，AC算法从某种程度上可以说是KMP算法在多模式环境下的扩展。
　　
　　如果要用KMP算法匹配长度为n的文本中的m个模式，则需要为每一个模式维护一个next跳转表，在执行对文本的匹配过程中，我们需要关注所有这些next表的状态转移情况，这使得时间复杂度增长为O(mn)，对于较大的模式集合来说，这样的时间增长可能是无法接受的。AC算法解决了这一问题，通过对模式集合P的预处理，去除了模式集合的规模对匹配算法速度的影响。
　　

AC定义:

AC有限自动机 M 是1个6元组：M =(Q，∑，g，f，qo，F)其中：

1、Q是有限状态集(模式树上的所有节点).
2、∑是有限的输入字符表(模式树所有边上的字符).
3、g是转移函数.
4、f是失效函数，不匹配时自动机的状态转移.
5、qo∈Q是初态(根节点);
6、F量Q是终态集(以模式为标签的节点集).

AC算法思想

　　多模式匹配AC算法的核心仍然是寻找模式串内部规律，达到在每次失配时的高效跳转。这一点与单模式匹配KMP算法和BM算法是一致的。不同的是，AC算法寻找的是模式串之间的相同前缀关系。
　　
　　要理解AC算法，仍然需要对KMP算法的透彻理解。那么前缀自包含如何在AC算法中发挥作用？
　　
　　在KMP算法中，对于模式串”abcabcacab”，我们知道非前缀子串abc(abca)cab是模式串的一个前缀(abca)bcacab，而非前缀子串ab(cabca)cab不是模式串abcabcacab的前缀，根据此点，我们构造了next结构，实现在匹配失败时的跳转。
　　
　　而在多模式环境中，这个情况会发生一定的变化。
　　对于模式集合P{he，she，his，hers}，模式s(he)的非前缀子串he，实际上却是模式(he)，(he)rs的前缀。如果目标串target[i…i+2]与模式she匹配，同时也意味着target[i+1…i+2]与he，hers这两个模式的头两个字符匹配，所以此时对于target[i+3]，我们不需要回溯目标串的当前位置，而直接将其与he，hers两个模式的第3个字符对齐，然后直接向后继续执行匹配操作
　　
　　经典的AC算法由三部分构成，goto表，fail表和output表，共包含四种具体的算法，分别是计算三张查找表的算法以及AC算法本身。
　　goto表是由模式集合P中的所有模式构成的状态转移自动机。
　　failure表作用是在goto表中匹配失败后状态跳转的依据，这点与KMP中next表的作用相似。
　　output表示输出，又称：emits，即代表到达某个状态后某个模式串匹配成功

构造goto表

　　goto表是由模式集合P中的所有模式构成的状态转移自动机，本质上是一个有限状态机，这里称作模式匹配机（Pattern Matching Machine，PMM）。
　　
　　对于给定的集合P{p1,p2,…pm}，构建goto表的步骤是，对于P中的每一个模式pi[1…j]（1 <= i < m+1)），按照其包含的字母从前到后依次输入自动机，起始状态D[0]，如果自动机的当前状态D[p]，对于pi中的当前字母pi[k]（1<=k<=j），没有可用的转移，则将状态机的总状态数smax+1，并将当前状态输入pi[k]后的转移位置，置为D[p][pi[k]] = smax，如果存在可用的转移方案D[p][pi[k]]=q，则转移到状态D[q]，同时取出模式串的下一个字母pi[k+1]，继续进行上面的判断过程。这里我们所说的没有可用的转移方案，等同于转移到状态机D的初始状态D[0]，即对于自动机状态D[p]，输入字符pi[k]，有D[p][pi[k]]=0。
　　
　　对于模式集合P{he，she，his，hers}， goto表的构建过程如下：
　　
　　1、PMM初始状态为0，然后向PMM中加入第一个模式串K[0] = “he”。
　　
　　　　
　　
　　2、继续向PMM中添加第二个模式串K[1] = “she”，每次添加都是从状态0开始扫描。
　　
　　　　
　　
　　3、从状态0开始继续添加第三个模式串K[2] = “his”，这里值得注意的是遇到相同字符跳转时要重复利用以前已经生成的跳转。如这里的’h’在第一步中已经存在。
　　
　　　　
　　
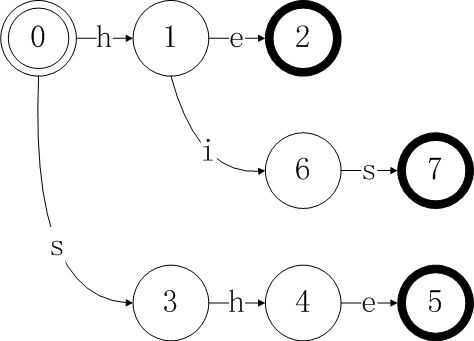
　　4、添加模式串K[3] = “hers”。至此，goto表已经构造完成。
　　
　　　　

　　对于第一和第二步而言，两个模式没有重叠的前缀部分，所以每输入一个字符，都对应一个新状态。第三步时，我们发现，D[0][p3[1]]=D[0][‘h’]=1，所以对于新模式p3的首字母’h’，我们不需要新增加一个状态，而只需将D的当前状态转移到D[1]即可。而对于模式p4其前两个字符he使状态机转移至状态D[2]，所以其第三字符对应的状态D[8]就紧跟在D[2]之后。

构造failure表

　　failure表作用是在goto表中匹配失败后状态跳转的依据，这点与KMP中next表的作用相似。
　　
　　首先说明什么状态，在上面goto表的图里，把圆圈里的数字记为状态。
　　
　　再引入状态深度的概念，状态s的深度depth(s)定义为在goto表中从起始状态0到状态s的最短路径长度。如goto表中状态1和3的深度为1。
　　
　　计算思路：先计算所有深度是1的状态的失效函数值，然后计算所有深度为2的状态，以此类推，直到所有状态（除了状态0，因为它的失效函数没有定义）的失效函数值都被计算出。

　　计算方法：用于计算某个状态失效函数值的算法在概念上是非常简单的。首先，令所有深度为1的状态s的函数值为f(s) = 0。假设所有深度小于d的状态的f值都已经被算出了，那么深度为d的状态的失效函数值将根据深度小于d的状态的失效函数值来计算。
　
　　具体步骤:　构造failure表利用到了递归的思想。

1、若depth(s) = 1，则f(s) = 0；即与状态0距离为1（即深度为1）的所有状态的fail值都为0
2、假设深度为d-1的所有状态r, 即depth(r) < d，已经计算出了f(r)；
3、那么对于深度为d的状态s：
　　(1) 若所有的字符a， 满足g(r,a) = fail，则不动作；（注：g为状态转移函数）；
　　(2) 否则，对每个使 g(r, a) = s成立的字符a，执行以下操作:：
　　 　　a、使state = f(r)
　　　　 b、重复步骤state = f(state)，直到g(state, a) != fail。（注意对于任意的a，状态0的g(0,a) != fail）
　　　　 c、使f(s) = g(state, a)。

　　例子: 求状态4 的failure 状态，已知其前一个(父节点)的f(1)= 0,且状态0(根节点)有字符’h’的外向边,该外向边对应状态1,则有f(4) = 1;类似前缀规则:求已经匹配字串”sh” 最大后缀,同时是某个模式串的前缀;

　　根据以上算法，得到该例子的failure表为：
　　i　　1　　2　　3 　　4 　　5　　6　　7　　8　　9
　　f(i)　0　　0　　0 　　1　　 2　　0　　3　　0　　3
　　　
　　将failure表用虚线表现，整合goto表，得到下图：
　　　　

构造output表

　　output表示输出，即代表到达某个状态后某个模式串匹配成功。该表的构造过程融合在goto表和failure表的构造过程中。
　　
　　 1、在构造goto表时，每个模式串结束的状态都加入到output表中，也就goto表中的黑色加粗圆圈。得到
　　　　 i 　　 output(i)
　　 　　2 　　{he}
　　 　　5　　 {she}
　　 　　7　　 {his}
　　 　　9　　 {hers}
　　 2、在构造failure表时，若f(s) = s’，则将s和s‘对应的output集合求并集。如f(5) = 2，则得到最终的output表为：
　　 　　 i　　 output(i)
　　 　　 2　　 {he}
　　 　　 5　　 {she，he}
　　 　　 7　　 {his}
　　 　　 9　　 {hers}

AC算法匹配过程

　　
　　 自动机从根节点0出发
　　 1、首先尝试按success表转移（图中实线）。按照文本的指示转移，也就是接收一个u。此时success表中并没有相应路线，转移失败。
　　 2、失败了则按照failure表回去（图中虚线）。按照文本指示，这次接收一个s，转移到状态3。
　　 3、成功了继续按success表转移，直到失败跳转步骤2，或者遇到output表中标明的“可输出状态”（图中红色状态）。此时输出匹配到的模式串，然后将此状态视作普通的状态继续转移。

　　 根据上面已经构造好的goto、failure和output表。以字符串”ushers”为例。状态转移如下：
　　　　 　　 u　　 s　　 h　　 e　　 r　　 s
　　　　 0　　0　　 3　　 4　　5　　8　　 9
　　 　　 　　 　　 　　 　　 　 2
　　 说明：在状态5发生失配，查找failure表，转到状态2继续比较。在状态5和状态9有输出。
　　
　　 算法高效之处在于，当自动机接受了“ushe”之后，再接受一个r会导致无法按照success表转移，此时自动机会聪明地按照failure表转移到2号状态，并经过几次转移后输出“hers”。来到2号状态的路不止一条，从根节点一路往下，“h→e”也可以到达。而这个“he”恰好是“ushe”的结尾，状态机就仿佛是压根就没失败过（没有接受r），也没有接受过中间的字符“us”，直接就从初始状态按照“he”的路径走过来一样（到达同一节点，状态完全相同）。

AC算法具体实现：

robert-bor实现的ac算法(java)：https://github.com/robert-bor/aho-corasick
hankcs改进robert-bor的ac算法(java)：https://github.com/hankcs/aho-corasick。

简单实现java：

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.Hashtable;
import java.util.List;

public class ACTest {

    static String Text = "ushers";
    static String[] Pattens = {"he", "she", "his", "hers"};
    // 根节点
    static TreeNode root; 

    public static void main(String[] args) {
        buildGotoTree(); // 构建goto表和output表
        addFailure();    // 构建failure表
        printTree();     // 打印tree的字符、深度、状态，fail值
        acSearch();      // 查找ushers， 并打印匹配的位置和模式
    }

    /**
     * 构建Goto表和output表
     */
    public static void buildGotoTree(){
        int i = 1;
        root = new TreeNode(null, ' ');
        // 判断节点是否存在， 存在转移 ，不存在添加   
        for (String word : Pattens) { 
            TreeNode temp = root;
            for (char ch : word.toCharArray()) {  
                TreeNode innerTem = temp.getSonNode(ch);
                if(innerTem == null){
                    TreeNode newNode = new TreeNode(temp, ch); 
                    newNode.setStatus(i++);
                    temp.addSonNode(newNode);  
                    innerTem = newNode;  
                }
                temp = innerTem;
            }  
            temp.addResult(word);
        }  
    }

    /**
     * 构建failure表
     * 遍历所有节点, 设置失败节点 原则: 节点的失败指针在父节点的失败指针的子节点中查找 最大后缀匹
     */
    public static void addFailure(){
        // 过程容器  
        ArrayList mid = new ArrayList();

        // 首先，设置二层失败指针为根节点 收集三层节点。 即令所有深度为1的状态s的函数值为f(s) = 0。 
        for (TreeNode node : root.getSons()) {  
            node.setFailure(root);  
            for (TreeNode treeNode : node.getSons()) {  
                mid.add(treeNode);  
            }  
        }  

        // 广度遍历所有节点设置失败指针 1.存在失败指针 2.不存在到root结束  
        while(mid.size() > 0){  
            // 子节点收集器
            ArrayList temp = new ArrayList();  
            for (TreeNode node : mid) {  
                TreeNode r = node.getParent().getFailure();  
                // 没有找到,保证最大后缀 (最后一个节点字符相同)  
                while(r != null && r.getSonNode(node.getCh()) == null){  
                    r = r.getFailure();
                }  

                // 是根结节点
                if(r == null){  
                    node.setFailure(root);  
                }else{  
                    node.setFailure(r.getSonNode(node.getCh()));  
                    // 重叠后缀的包含  
                    for (String result : node.getFailure().getResults()) {  
                        node.addResult(result);  
                    }  
                }  
                // 收集子节点  
                temp.addAll(node.getSons());  
            }  
            mid = temp;  
        }  
    }

    /**
     * 根据状态顺序打印树信息
     */
    public static void printTree(){
        // 收集所有节点
        List nodesList = new ArrayList();
        // 过程容器 
        List nodes = Arrays.asList(root);
        while(nodes.size() > 0){
            ArrayList temp = new ArrayList();  
            for(TreeNode node : nodes){
                temp.addAll(node.getSons());
                nodesList.add(node);
            }
            nodes = temp;
        }
        // 排序
        Collections.sort(nodesList, (a, b) -> a.getStatus().compareTo(b.getStatus()));
        for(TreeNode node : nodesList){
            System.out.println(node.getCh() + " " + node.getDepth() + " " + node.getStatus() + 
                    " " + (node.getFailure() != null ? node.getFailure().getStatus() : "0"));
        }
    }

    // 查找全部的模式串  
    public static void acSearch(){
        // 可以找到 转移到下个节点 不能找到在失败指针节点中查找直到为root节点  
        int index = 0;  
        TreeNode mid = root;  
        while(index < Text.length()){  
            TreeNode temp = null;  

            while(temp ==null){  
                temp = mid.getSonNode(Text.charAt(index));  
                if(mid ==root){  
                    break;  
                }  
                if(temp==null){  
                    mid = mid.getFailure();  
                }  
            }  
            // mid为root 再次进入循环 不需要处理  或者 temp不为空找到节点 节点位移  
            if (temp != null) mid = temp;

            for (String result : mid.getResults()) {  
                System.out.println((index - result.length() + 1) + ":" + index + "=" + result);
            }  
            index++;  
        }  
    } 
}

class TreeNode{
    // 父节点
    private TreeNode parent;
    // failuere
    private TreeNode failure;
    // 字符
    private char ch;
    // goto表
    private List sons;
    // 获取子节点
    private Hashtable sonsHash;  
    // output
    private List results;
    // 深度
    private int depth = 0;
    // 状态
    private Integer status = 0;

    public TreeNode(TreeNode parent, char ch) {  
        this.parent = parent;  
        this.ch = ch;  
        results = new ArrayList();  
        sonsHash = new Hashtable();  
        sons = new ArrayList();
        if(parent != null)
            depth = parent.getDepth() + 1;
    }  

    // 添加一个结果到结果字符中, 状态5量 output : he 和 she
    public void addResult(String result){  
          if(!results.contains(result)) results.add(result); 
    }

    // 添加子节点  
    public void addSonNode(TreeNode node){  
        sonsHash.put(node.ch, node);  
        sons.add(node);
    }  

    // 设置失败指针并且返回  
    public TreeNode setFailure(TreeNode failure){  
        this.failure = failure;  
        return this.failure;  
    }  

    // 获取子节点中指定字符节点  
    public TreeNode getSonNode(char ch){  
        return sonsHash.get(ch);  
    }  

    // 获取父节点
    public TreeNode getParent() {
        return parent;
    }
    // 获取字符
    public char getCh() {
        return ch;
    }
    // 获取所有的孩子节点  
    public List getSons() {
        return sons;
    }
    // 获取搜索的字符串  
    public List getResults() {
        return results;
    }
    // 获取深度
    public int getDepth() {
        return depth;
    }
    public Integer getStatus() {
        return status;
    }
    public void setStatus(Integer status) {
        this.status = status;
    }
    public TreeNode getFailure() {
        return failure;
    }
}

心得：

　　KMP算法依然是解读AC算法的重要线索，前缀，子串，后缀永远和模式匹配纠缠在一起。
　　
　　AC状态机实际上更适合用Trie结构来存储。
　　
　　可以将算法中使用到的goto，fail，output三张表以离线的方式计算出来保存在一个文件中，当AC算法启动时，直接从文件中读取三个表的内容，这样可以有效减少每次AC算法启动时都需要构建三个表所花费的时间。
　　
　　可以把同深度节点排序，后面查找某状态的指定字符外向边状态，可以使用二分查找，加快速度;

　　值得注意的是在AC算法的以上实现中，对于输入字符a的跳转次数是不确定的。因为有可能在输入a后发生失配，需要查找failure表重新跳转。能不能在PMM的基础上实现确定型的有限状态机，即对于任意字符a，都只用进行一次确定的状态跳转？答案是肯定的。在Aho和Corasick论文中给出了处理的方法：构造一个与KMP算法中相似的next表，实现确定性跳转。