广度优先搜索(BFS)分分钟让你学会BFS!!!

BFS—从入门到精通

什么是BFS

对于一棵树,一般有两种方法去遍历一棵树,一种是深度优先搜索(DFS),还有一种就是我们今天要讲的广度优先搜索(BFS)啦.
对于深度优先搜索,我们在这里不做详细讲解,有兴趣的童鞋可以到这里看看哦.
好了,回到正题,所谓广度优先搜索,顾名思义就是通过广度的大小来决定搜索的顺序了(既从深度小的开始搜,再搜深度大的).什么意思??看到这里,可能有些童鞋还没看懂,下面举一个详细的例子.

(这可是灵魂画师的手笔哦,是有点丑,不要介意)
对于一棵树(such this),我们可以选择一个节点作为它的根节点,就以1为根节点为例.
首先,我们先访问根节点1,将它加入队列G中.(将它标记为蓝色表示访问过了)

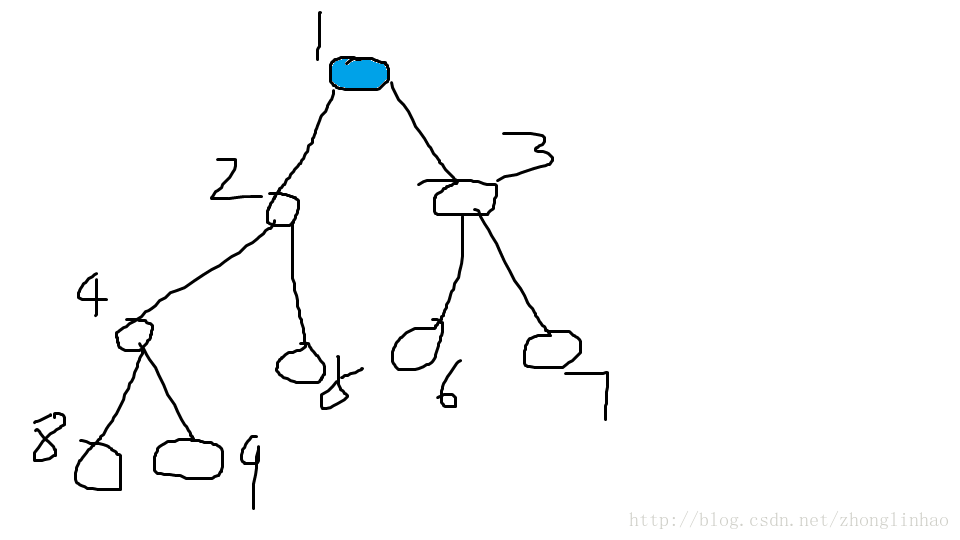
此时队列中有{1}一个元素.
然后将队列G中的头元素取出,发现它有2,3两个子节点,将其先后加入到队列中.

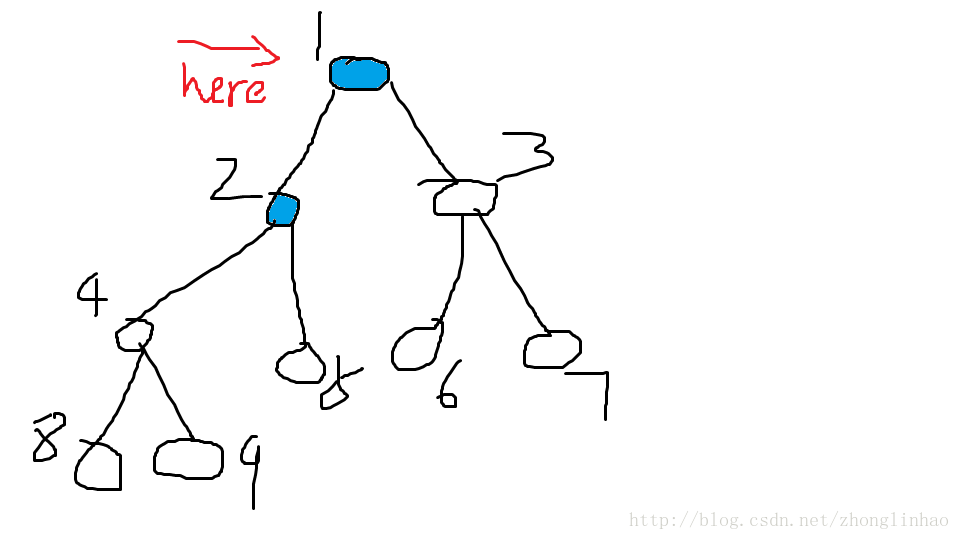
此时队列G中有{2}1个元素(1这个元素已经被取出了)
取出的元素有{1}

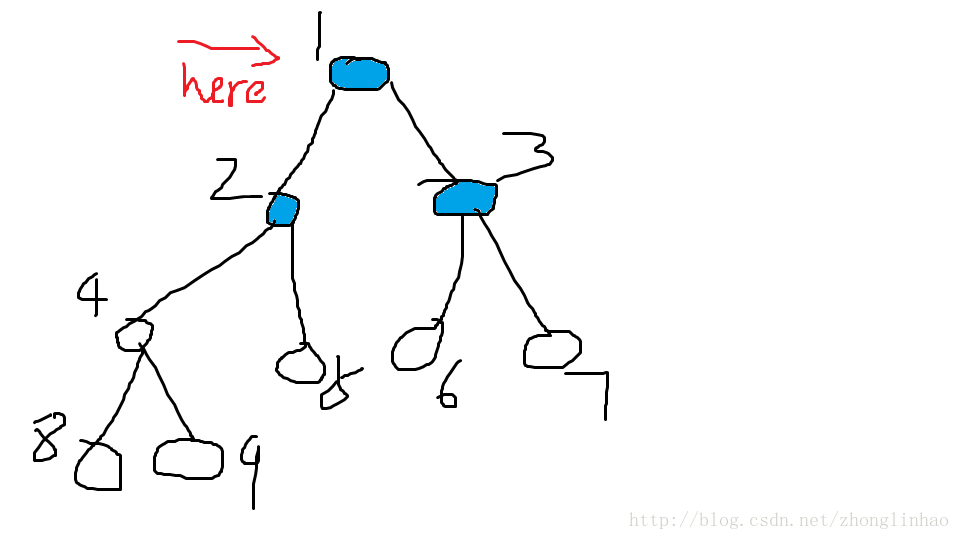
此时队列G中有{2,3}1个元素
取出的元素有{1}
现在我们遍历完1的子节点了,再将队列G中的头元素(2)取出进行上述操作

此时队列G中有{3,4}2个元素
取出的元素有{1,2}

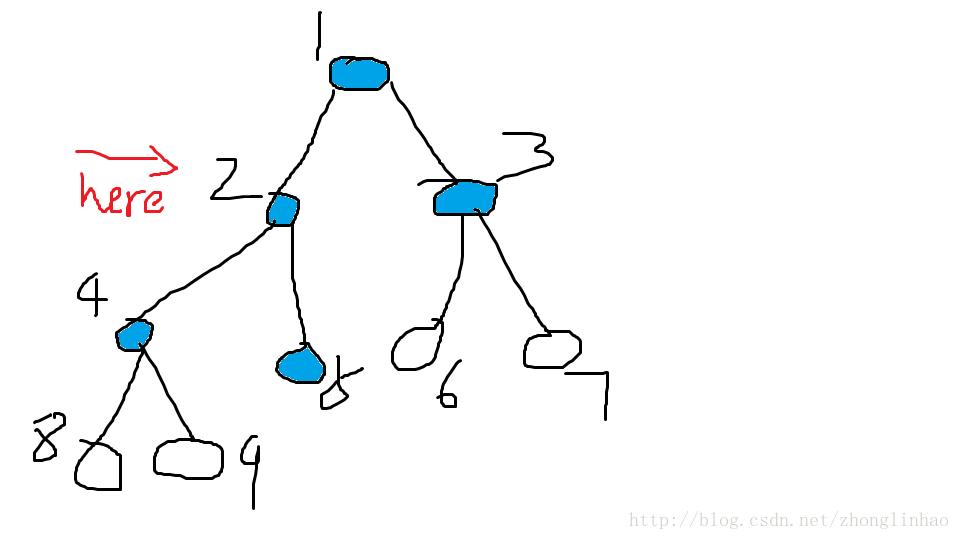
此时队列G中有{3,4,5}3个元素
取出的元素有{1,2}
然后是一样的操作啦.

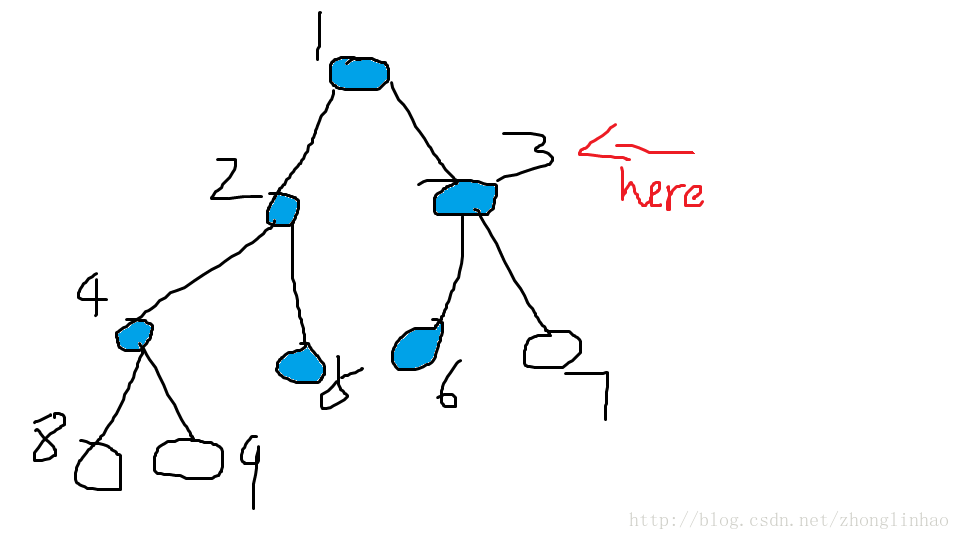
此时队列G中有{4,5,6}3个元素
取出的元素有{1,2,3}

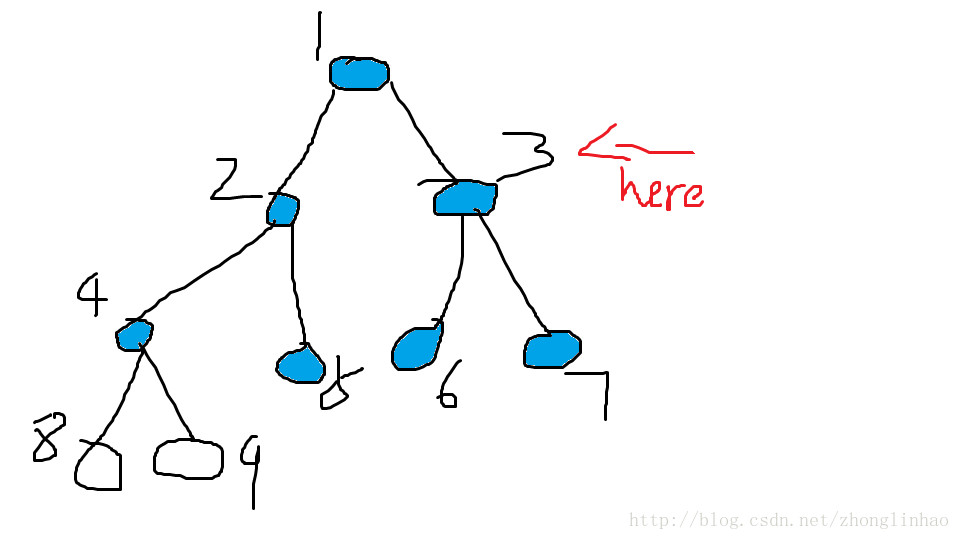
此时队列G中有{4,5,6,7}4个元素
取出的元素有{1,2,3}

此时队列G中有{5,6,7,8}4个元素
取出的元素有{1,2,3,4}

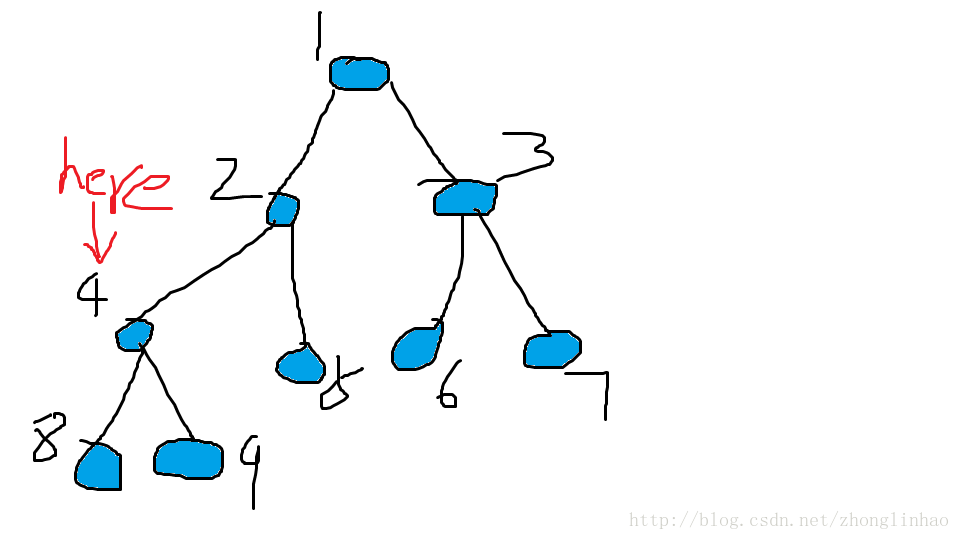
此时队列G中有{5,6,7,8,9}5个元素
取出的元素有{1,2,3,4}
哎呀,接下来将5取出,可是5没有子节点,这该怎么办呢?
并没有关系,你可以直接将5取出
此时队列中有{6,7,8,9}5个元素
取出的元素有{1,2,3,4,5}
同理,依次取出6,7,8,9,最后得到的序列就是{1,2,3,4,5,6,7,8,9}了,是不是很神奇呢.
下面附上实现的代码

void BFS() {
    q.push(1);//q是一个队列用来储存拜访过的数(既上文的G)
    vis[1]=1;将其标记为已拜访过(在此处无用,但在做题的时候常常会用到)
    while(!q.empty()) {//如果队列没有空,既
        if(q.empty())break;
        int now=q.front();
        q.pop();//将q队列中的头元素取出,然后在q队列中删掉
        ans[++cnt]=now;//记录答案的顺序(既上文取出的元素顺序)
        for(int i=0; i//w[now][i]记录now节点的子节点
            q.push(w[now][i]);//将遍历的子节点加入到去q队列中
            vis[w[now][i]]=1;//将其标记为已拜访过(在此处无用,但在做题的时候常常会用到)
        }
    }
    return;
}

BFS小练(初入茅庐)

Catch That Cow

poj-3278

题意

一位农夫在点n上,他要到奶牛所在的点k上,他可以每次从点X到点X-1或点X+1或点2*X,问他到达点k的最短次数.(0 ≤ N ≤ 100,000,0 ≤ K ≤ 100,000)
样例:
Sample Input
5 17
Sample Output
4

思路

看到这一道题,我的第一反应就是看看能否找到规律,然而很显然它没有规律可言,我们需要靠一种近似暴力的方法,而DFS在这里是行不通的,于是只能用BFS来解这道题了.

code

#include 
#include 
#include 
#include
#define pp pair
using namespace std;
int n,k,ans;
queueq;
bool v[200004];
void bfs() {
    q.push(pp(n,0));//先将n丢进队列
    v[n]=1;
    while(!q.empty()) {
        if(q.empty())break;
        pp now=q.front();
        q.pop();
        if(now.first==k) {
            ans=now.second;
            break;
        }
        now.second++;//接下来我们有3种操作,将现在的位置now.second 加1 或 减1 或 乘2
        if(!v[now.first+1]&&now.first//边界条件不能少了
            q.push(pp(now.first+1,now.second));
            v[now.first+1]=1;//将已经走过的点标记为1,为什么呢??q队列中到这个数的次数是从小到大排序的,now.first+1这个点刚通过now.first被拜访过,它的此时次数肯定小于等于下一次拜访的次数.想一想为什么.
        }
        if(!v[now.first-1]&&now.first-1>=0) {
            q.push(pp(now.first-1,now.second));
            v[now.first-1]=1;
        }
        if(now.first2])) {
            q.push(pp(now.first*2,now.second));
            v[now.first*2]=1;
        }
    }
    return;
}
int main() {
    scanf("%d%d",&n,&k);
    bfs();
    printf("%d\n",ans);
    return 0;
}

这样题目就打完了,看到这里是不是有一种亲切感呢??v[]数组在这里体现了它的作用.
相关题目有:poj-1915;有兴趣的童鞋可以做一做哦.

BFS小练(崭露头角)

Prime Path

poj-3126

题意

给你两个四位数的质数a,b,让你通过一个操作使a变成b.这个操作可以使你当前的数x改变一位上的数使其变成另一个质数,问操作的最小次数(如果没有这种方式,输出Impossible)
注意:没有前导0!!!;
例如:1033到8179可以从1033->1733->3733->3739->3779->8779->8179
样例:
Sample Input
3
1033 8179
1373 8017
1033 1033
Sample Output
6
7
0

思路

看到这题目,我顿时懵了一下.这题目貌似无法用普通的方法写出.我看了好久才想到方法.这题目想要将其与BFS联系起来真的有点难.其实可以先将10000以内所有的质数记录下来,再进行BFS

code

#include
#include
#include
#include
#include
#define N 10003
#define pp pair
using namespace std;
int T,n,m,ans;
bool v[N],vis[N],t[N];
queueq;
void pre() {//记录10000以内的质数
    for(int i=2; i<=9999; i++) {
        if(!v[i]) {
            t[i]=1;//t[i]=1表示i是质数
            for(int j=i; j<=9999; j+=i) {
                v[j]=1;
            }
        }
    }
}
void BFS() {
    q.push(pp(n,0));//先将给我们的初始数加入q队列
    while(!q.empty()) {
        while(!q.empty()&&vis[q.front().first])q.pop();
        if(q.empty())break;
        pp now=q.front();
        vis[q.front().first]=1;
        q.pop();
        if(now.first==m) {
            ans=now.second;
            break;
        }
        for(int i=1; i<=1000; i*=10) {//枚举位数
            int r=now.first-((now.first/i)%10)*i;
            for(int j=0; j<=9; j++) {//枚举当前位数更改的值
                if(i==1000&&j==0)continue;//特判前导0的情况!!!
                if(t[r+j*i]&&!vis[r+j*i]) {
                    q.push(pp(r+j*i,now.second+1));//BFS的核心转移代码
                }
            }
        }
    }
    return;
}
int main() {
    pre();
    scanf("%d",&T);
    while(T--) {
        while(!q.empty())q.pop();
        memset(vis,0,sizeof vis);
        ans=-1;
        scanf("%d%d",&n,&m);
        BFS();
        if(ans==-1)printf("Impossible\n");
        else printf("%d\n",ans);
    }
    return 0;
}

相关题目有:poj-3669;有兴趣的童鞋可以做一做哦.

BFS小练(登堂入室)

Eight

poj-1077

题意

就是经典的八数码问题啦,给你一个状态s(such as{2 3 4}{1 5 x}{7 6 8} ),使其变成{1,2,3}{4,5,6}{7,8,x}的路径(左为l,右为r,上为u,下为d);
样例
Sample Input
2 3 4 1 5 x 7 6 8
Sample Output
ullddrurdllurdruldr

思路

这题卡了我很久,最后还是在其他大佬的帮助下才写出来的.这一题可以用康托展开来写(不知道的同学请点击here查看哦).我们可以将八数码的每一种状态通过康托展开的方法用一个数字表示出来,进行状态转移.但这不是重点!!!,我们重点是看它BFS是怎么打的.其他的不说了,代码中已经很详细了.

code

#include
#include
#include
#include
#define N 400000
using namespace std;
char s[10],lu[N],ans[N];
int a[10],jc[10],mark,dx[4]= {-3,-1,3,1},last[N],tt,flag;
struct node {
    int s[10];
} w;
bool v[N];
queueq;
int build(int a[]) {
    int sum=0;
    for(int i=1; i<=9; i++) {
        int r=0;
        for(int j=i+1; j<=9; j++) {
            if(a[j]9-i];//这里是康托展开的部分,sum是通过一个数表示着a数组的状态
    }
    return sum;
}
void pre() {
    jc[1]=1;
    for(int i=2; i<=9; i++) {
        jc[i]=jc[i-1]*i;//这里预处理出了1~9的阶乘
    }
}
void BFS() {
    node temp;
    for(int i=1; i<=9; i++)temp.s[i]=a[i];
    q.push(temp);
    mark=build(temp.s);
    v[mark]=1;
    while(!q.empty()) {
        node now=q.front();
        mark=build(now.s);
        q.pop();
        for(int i=1; i<=9; i++)temp.s[i]=now.s[i];
        int cnt;
        for(int i=1; i<=9; i++) {//找到9所在的位置
            if(now.s[i]==9) {
                cnt=i;
                break;
            }
        }
        for(int i=0; i<4; i++) {
            if(i==0&&(cnt-3)>=1||i==1&&(cnt%3)!=1||i==2&&(cnt+3)<=9||i==3&&(cnt%3)!=0) {//边界条件,不能丢!!!
                swap(temp.s[cnt],temp.s[cnt+dx[i]]);/进行状态转移
                int f=build(temp.s);
                if(!v[f]) {
                    v[f]=1;
                    last[f]=mark;
                    if(i==0)lu[f]='u';
                    if(i==1)lu[f]='l';
                    if(i==2)lu[f]='d';
                    if(i==3)lu[f]='r';//这里lu[f]表示到一个状态到状态f是向上向下向左向右4种中哪一种情况转换而来的
                    q.push(temp);//将符合的状态加入q队列
                }
                if(f==0) {//如果到达我们所要的结果({1,2,3}{4,5,6}{7,8,9}的状态表示值为0),就返回
                    flag=1;
                    return;
                }
                swap(temp.s[cnt],temp.s[cnt+dx[i]]);//返回之前的状态
            }
        }
    }
    return;
}
int main() {
    pre();
    int n;
    for(int i=1; i<=9; i++) {
        cin>>s[i];
        if(s[i]=='x')a[i]=9;//将x变成9,便于接下来的计算
        else a[i]=s[i]-'0';
    }
    BFS();
    if(!flag) {
        printf("unsolvable\n");
        return 0;
    }
    mark=build(a);
    int now=0;
    while(1) {
        if(now==mark)break;//递推求出路径
        ans[++tt]=lu[now];
        now=last[now];
    }
    for(int i=tt; i>=1; i--) {
        printf("%c",ans[i]);
    }
    printf("\n");
    return 0;
}

相关题目有:poj-1475;有兴趣的童鞋可以做一做哦.
希望这篇文章对你们有所帮助吧,小编在此与你们说再见了.>﹏<