对迪杰斯特拉算法的理解

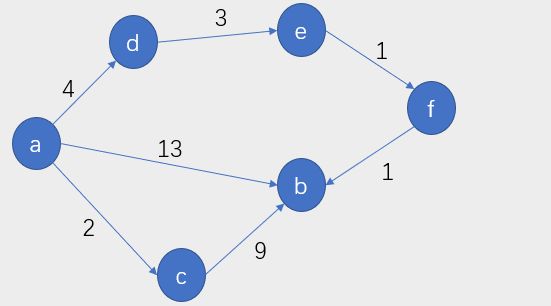
迪杰斯特拉算法的作用：

计算图中某个顶点到其他顶点的最短路径，边的权值不能为负数

 

 迪杰斯特拉算法的基本思想及代码介绍：

https://www.cnblogs.com/skywang12345/p/3711512.html

 

 

迪杰斯特拉算法的正确性证明：

数学上的证明：https://www.zhihu.com/question/20630094 

扣鼎之歌的回答 清晰地证明了dist[j] = min{dist[j], dist[i] + matrix[i][j]} 

 

贪心算法的最优子结构性质：https://zhidao.baidu.com/question/489320921946816252.html 

整体最优必定局部最优，但并不是所有局部最优解都被整体最优解包含

 

根据上述资料可以了解到，每当确定了一个顶点（初始顶点也算在内）的最短路径，并对所有已找到最短路径的顶点的邻居顶点进行调整后，下一个顶点的最短路径也就确定了

 

例子如下：

 

 

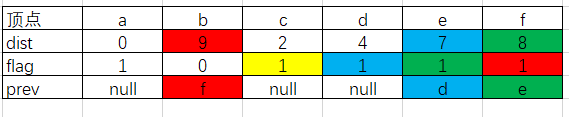
初始状态：

 

 

在flag=0的顶点中比较dist，选择顶点c（可以看到c是a的邻居顶点），令c的flag=1，改变其他顶点的dist，如下：

 

 

 

 

 

选择顶点d（d也是a，c的邻居顶点），操作同上：

 

 选择顶点e（e是a，c，d的邻居顶点），操作同上：

 

 

选择顶点f（f是a，c，d，e的邻居顶点），操作同上：

 

 选择顶点b，这时所有的顶点找到了最短路径，结束

 

 

例题：

租用游艇问题     完完全全的套dijkstra

#include 

#define MAXSIZE 200
#define INF 32767
void mindis(int(*matrix)[MAXSIZE], int start, int num)
{
    int dist[MAXSIZE], flag[MAXSIZE];
    int point=0;
    for (int i = 1; i <= num; i++)
    {
        dist[i] = matrix[start][i];
        flag[i] = 0;
    }
    flag[start] = 1;
    dist[start] = 0;
    for (int i = 1; i < num; i++)
    {
        int min = INF;
        for (int i = 1; (i <= num); i++)
        {
            if ((dist[i] < min) && (flag[i] == 0))
            {
                min = dist[i];
                point = i;
            }
        }
        flag[point] = 1;
        for (int j = 1; j <= num; j++)
            if (flag[j] == 0 && dist[j] > min + matrix[point][j])
                dist[j] = min + matrix[point][j];
    }
    printf("%d", dist[num]);

}

int main()
{
    int matrix[MAXSIZE][MAXSIZE],n;
    scanf("%d", &n);
    for (int i = 0; i < MAXSIZE; i++)
        for (int j = 0; j < MAXSIZE; j++)
        {
            if (i == j)
                matrix[i][j] = 0;
            else
                matrix[i][j] = INF;
        }
    for (int i = 1; i < n; i++)
        for (int j = i + 1; j <= n; j++)
            scanf("%d", &matrix[i][j]);
    mindis(matrix, 1, n);
    return 0;
}