计算机组成原理个人总结(2)
数据的表示和运算
- (一)数制与编码
- 进位计数制及其相互转换
- 进制:
- 不同进制数之间的相互转换
- 真值和机器数
- BCD码
- 字符与字符串(了解)
- 校验码
- 1.奇偶校验码
- 海明(汉明)校验码
- 循环冗余校验(CRC)码
- 相关一些知识
- 源补码的转换规律
- 定点数的运算
- 源码定点数的加减法运算
- 定点数的乘法运算
- 原码一位乘法
- 补码一位乘法
- 定点数的除法运算
- 原码除法运算(不恢复余数法)
- 补码除法运算(加减交替法)
(一)数制与编码
进位计数制及其相互转换
进制:
- 二进制。计算机中用得最多的是基数为2的计数制,即二进制。二进制只有0和1两种
数字符号,计数“逢二进一”。它的任意数位的权为2i, i为所在位数。 - 八进制。八进制作为二进制的一种书写形式,其基数为8,有0~7共8个不同的数字符
号,计数“逢八进一”。 因为r=8=23, 所以只要把二进制中的3位数码编为组就是一
位八进制数码,两者之间的转换极为方便。 - 十六进制。十六进制也是一进制的一 种常用书写形式, 其基数为16,“逢十六进一”。每个
数位可取0-9.A.B、C.D、E、F中的任意一个,其中A、B、C、D、E、F分别表示10~15。因为r=16=24,因此4位进制数码与1位十六进制数码相对应
不同进制数之间的相互转换
(1)二进制数转换为八进制数和十六进制数
在转换时应以小数点为界。
整数部分:在从小数点开始往左数,将一串二进制数分为3位(八进制)一组或4位(十六进制)一组,在数的最左边可根据需要加“0”补齐;对于小数部分,从小数点开始往右数,也将一串二进制分为3位一组或4位一组,在数的最右边也可以根据需要加“0”补齐。最终使总的位数为3或4的整数倍,然后分别用对应的八进制数或十六进制数取代;
例: 将二进制数 1111000010.01101 分别转换为八进制数和十六进制数
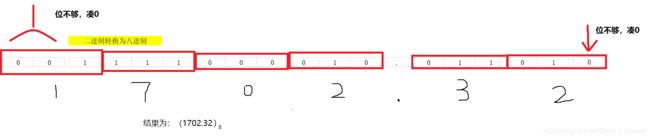

(2)任意进制数转换为十进制数
将各位数码与他们的权值相乘在相加。
(3)十进制数转换为任意进制数
通常采用基数相乘法,对整数部分用除基取余法,对小数部分用乘基取整法,最后将整数和小数拼接在一起。
例:将十进制数123.6875转换成二进制数
整数部分

小数部分:

结果为:(1111011.1011)2
注意:小数和整数不一样,整数可以连续表示,但小数是离散的。二进制的小数只能表示1/2,1/4,……,1/2n,因此无法表示所有的十进制小数。
真值和机器数
带“+”或“-”符号的数为真值。
用0,1这种表示正负的数称为机器数。
BCD码
二进制编码的十进制通常采用4位二进制数来表示一位十进制数中的0~9这十个数码。但4位二进制数可以组合出16种代码,因此必有6种状态为无效码。
(1)8421码:
权值按8,4,2,1由高到低来表示。若两个8421码相加之和小于等于(1001)2即(9)10,则不需要修正;若相加之和大于等于(1001)2即(9)10,则要加6修正(从1010到1111这六个为无效码)
(2)余3码
这个是在8421码的基础上加(0011)2形成的,因为每个数都余“3”,因此称为余3码。
(3)2421码
也是一种有权码,权值按2,4,2,1由高到低来表示。特点是大于等于5的4位二进制数中最高位为1,小于5的最高位为0.如5→1011而非0101.
字符与字符串(了解)
ASCII码:表示10个十进制数码,52个英文大写字母和小写字母以及一定量的专用符号(如$、%、^、&、*),共128个字符。
汉字的表示和编码
校验码
1.奇偶校验码
码距为等于2,可以检测出一位错误(或奇数位错误),但不能确定出错的位置,也不能够检测出偶数位错误,增加的冗余位称为奇偶校验位。
奇校验码:整个校验码(有效信息位和校验位中)“1”的个数为奇数。
偶校验码:整个校验码(有效信息位和校验位中)“0”的个数为偶数。
例 :
1001101 11001101(奇校验) 01001101(偶校验)
1010111 01010111(奇校验) 11010111(偶校验)
海明(汉明)校验码
实现原理:
在有效信息位中加入几个校验位形成海明码,并把海明码的每个二进制位分配到几个奇偶校验组中。当某一位出错后,就会引起有关的几个校验位的值发生变化,这不但可以发现错位,还能指出错位的位置,为自动纠错提供依据。
L-1=D+C且D>=C
L:编码最小码距 D:检测错误的位数 C:纠正错误的位数
在海明码中,为了达到检测和纠正一位错,校验的位数k应满足2k>=n+k+1,其中n为信息位的位数.若在纠正一位错的情况下还要能够发现两位错,则还需在增加一位校验位,即需要满足2k-1-1>=n+k
循环冗余校验(CRC)码
CRC接收端检测出某一位数据错误后,纠正的方法是:1.请求重发2.删除数据3.通过余数值自动纠正。
相关一些知识
- ASCII编码:使用8位二进制代码,最右边一位是0。
ASCII码由7位二进制代码表示,从000000到11111共128种编码。但由于字节是计算
机存储的基本单元,ASCI码仍以一字节存入一个ASCII字符,只是每字节中多余的一 位即最高
位(最左边-位)在机内部保持为“0”。 - 校验码:1.任意两个码字之间最少变化的二进制位数称为码距,码距大于等于2的数据校验码开始具有检错的能力。2.码距越大,检错、纠错能力越强。奇偶校验码的码距等于2,可以检测出一位错误(或奇数位错误),但不能确定出错的位置,也不能检测出偶数位错误;海明码的码距大于2,因此不仅可以发现错误,还能指出错误的位置。3.仅靠增加奇偶校验位的位数不能提高正确性,还要考虑码距。
- 在大量数据传送的过程中,常用且有效的校验法是CRC校验。
源补码的转换规律
定点数的运算
源码定点数的加减法运算
- 加法规则:先判符号位,若相同,则绝对值相加,结果符号位不变;若不同,则做减法,绝对值大的数减去绝对值小的数,结果符号位与绝对值大的数相同。
- 减法规则:两个原码表示的数相减,首先将减数与符号取反后的减数按原码加法进行运算。
- 注意:运算时注意机器字长,当左边位出现溢出时,将溢出位丢掉。
3.补码定点数加减法运算
- 参与运算的两个操作数均用补码表示。
- 按二进制运算规则运算,逢二进一。
- 符号位与数值位按同样规则一起参与运算,符号位运算产生的进位要丢掉,结果的符号位由运算得出。
- 补码加减运算依据下面的公式进行。当参加运算的数是定点小数时,模M=2;当参加运算的数是定点整数时,模M=2n+1。
[A+B]补=[A]补+[B]补(mod M)
[A-B]补=[A]补+[ - B]补(mod M)
注意:mod M运算是为了将溢出位丢掉。 - 补码运算的结果亦为补码。
定点数的乘法运算
原码一位乘法
原码一位乘法的特点是符号位与数值位是分开求的,乘积符号由两个数的符号位“异或”形成,而乘积的数值部分则是两个数的绝对值相乘之积。
设[X]原=xs.x1x2……xn,[Y]原=ys.y1y2……yn,则运算规则如下:
(1)被乘数和乘数均取绝对值参加运算,符号位为xs异或ys。
(2)部分积的长度同被乘数,取n+1位,以便存放乘法过程中绝对值大于等于1的值,初值为0.
(3)从乘数的最低位yn开始判断:若yn=1,则部分积加上被乘数|x|,然后右移一位;若yn=0,则部分积加上0,然后右移一位。
(4)重复步骤(3),判断n位
注意:考虑到运算时可能出现绝对值大于1的情况(但此刻并非溢出),所以部分积和被乘数取双符号位。
补码一位乘法
这是一种有符号数的乘法,采用相加和相减操作计算补码数据的乘积。
设[X]补=xs.x1x2……xn,[Y]补=ys.y1y2……yn,则运算规则如下:
(1)符号位参与运算,运算的数均以补码表示。
(2)被乘数一般取双符号位数进行运算,部分积取双符号位,初值为0,乘数可取单符号位。
(3)乘数末位增设附加位yn+1,且初值为0.
(4)根据(yn,yn+1)的取值来确定操作,见表2.2.
表2.2 Booth 算法的移位规则
| yn(高位) | yn+1(低位)) | 操作 |
|---|---|---|
| 0 | 0 | 部分积右移一位 |
| 0 | 1 | 部分积加[X]补,右移一位 |
| 1 | 0 | 部分积加[-X]补,右移一位 |
| 1 | 1 | 部分积右移一位 |
(5)移位按补码右移规则进行。
(6)按照上述算法进行n+1步操作,但第n+1步不再移位(共进行n+1次累加和n次右移),仅根据yn与yn+1的比较结果做相应的运算。
定点数的除法运算
在计算机中,除法运算可转换成“累加——左移”(逻辑左移),根据机器数的不同,可分为原码除法和补码除法。
原码除法运算(不恢复余数法)
原码除法主要采用原码不恢复余数法,也称原码加减交替除法。特点是商符和商值是分开进行的,商符由两个操作数的符号位“异或”形成。求商值的规则如下。
设被除数[X]原=xs.x1x2x3……xn,除数[Y]原=ys.y1y2y3……yn。
(1)商的符号:Qs=xs异或ys。
(2)商的数值:|Q|=|X|/|Y|。
求|Q|的不恢复余数法运算规则如下。
(1)符号位不参加运算。
(2)先用被除数减去除数(|X|-|Y|=|X|+(-|Y|)=|X|+|[-Y|]补),当余数为正时,商上1,余数和商左移一位,在减去除数;当余数为负时,商上0,余数和商左移一位,在加上除数。
(3)当第n+1步余数为负时,需加上|Y|得到第n+1步正确的余数(余数与被除数同号)。
补码除法运算(加减交替法)
补码一位除法的特点是,符号位与数值位一起参加运算,商符自然形成。除法第一步根据被除数和除数的符号决定是做加法还是减法;上商的原则根据余数和除数的符号位共同决定,同号上商“1”,异号上商“0”;最后一步商恒置“1”。
加减交替法的规则如下:
(1)符号位参加运算,除数与被除数均用补码表示,商和余数也用补码表示。
(2)若被除数与除数同号,则被除数减去除数;若被除数与除数异号,则被除数加上除数。
(3)若余数与除数同号,则商上1,余数左移一位减去除数;若余数与除数异号,则商上0,余数左移一位加上除数。
(4)重复执行第(3)步操作n次。
(5)若对商的精度没有特殊要求,则一般采用“末位恒置1”法。




