数据结构—无向图—通信网络的构建(c++)

实验内容

项目名称：通信网构建
项目内容：在 n 个城市之间建立通信联络网，则连通 n 个城市只需要 n-1 条线路。要求在 最节省经费的前提下建立这个通信网。
（1） 完成城市信息的输入。

（2） 完成城市信息的编辑，包括城市以及城市间距离的增加，删除，信息修改等。
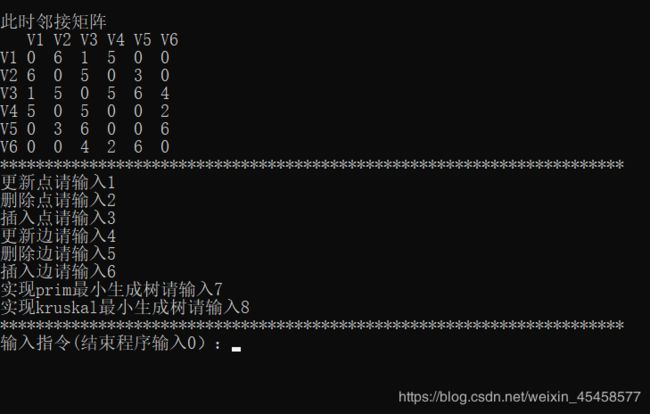
（3） 允许用户指定下列两种策略进行通信网的构建
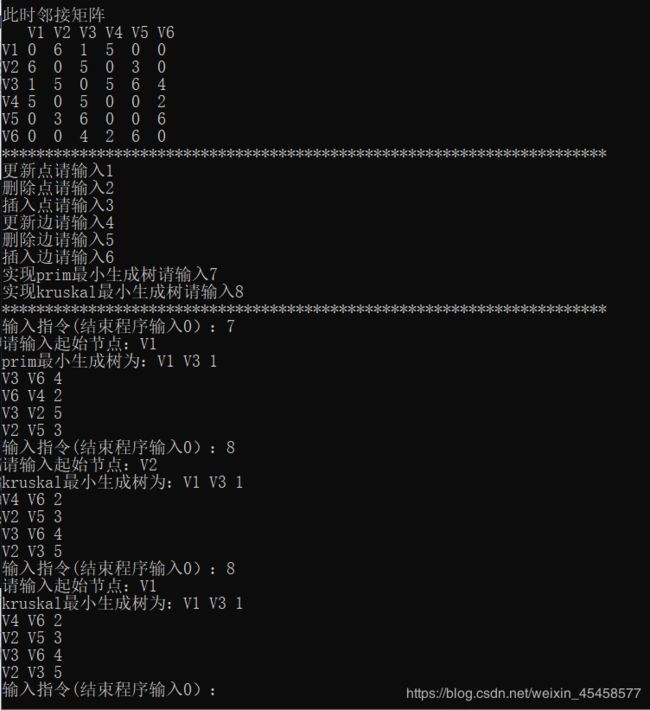
1）采用 Prim 算法进行通信网的构建；
2）采用 Kruskal 算法进行通信网的构建；

程序截图

开始时输入信息：

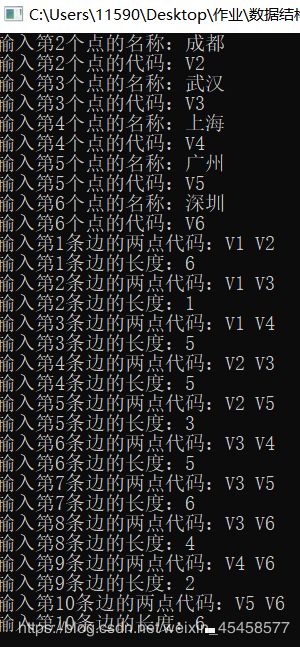
初始化完成后：

最小生成树：

也能对节点和边进行删改。

实现代码

main.cpp

#include"Graph.h"
#include
using namespace std;
void printmenu(Graph &a)
{
	cout << endl;
	a.CreateUDN();
	cout << "**********************************************************************" << endl;
	cout << "更新点请输入1" << endl << "删除点请输入2" << endl << "插入点请输入3" << endl;
	cout << "更新边请输入4" << endl << "删除边请输入5" << endl << "插入边请输入6" << endl;
	cout << "实现prim最小生成树请输入7" << endl << "实现kruskal最小生成树请输入8" << endl;
	cout << "**********************************************************************" << endl;
	cout << "输入指令(结束程序输入0）：";
}
int main()
{
	int command;
	Edge edge;
	Vex vex;
	cout << "输入图的点数和边数：";
	Graph a;
	system("cls");
	printmenu(a);
	while (true)
	{
		cin >> command;
		switch (command)
		{
		case 0:return 0;
		case 1:cout << "请输入要更新点的代码：";cin >> vex.Code;a.UpdateVex(a.GetVex(vex.Code));break;
		case 2:cout << "请输入要删除点的代码：";cin >> vex.Code;a.DeleteVex(a.GetVex(vex.Code));break;
		case 3:cout << "请输入要插入点的代码和名称：";cin >> vex.Code >> vex.Name;a.InsertVex(vex);break;
		case 4:cout << "请输入要更新边的2个点的代码：";cin >> edge.vex1.Code >> edge.vex2.Code;a.UpdateEdge(a.GetEdge(edge.vex1.Code,edge.vex2.Code));break;
		case 5:cout << "请输入要删除边的2个点的代码：";cin >> edge.vex1.Code >> edge.vex2.Code;a.DeleteEdge(a.GetEdge(edge.vex1.Code, edge.vex2.Code));break;
		case 6:cout << "请输入要插入边的2个点的代码和长度：";cin >> edge.vex1.Code >> edge.vex2.Code >>edge.weight;a.InsertEdge({ a.GetVex(edge.vex1.Code),a.GetVex(edge.vex2.Code),edge.weight});break;
		case 7:a.PrimMinTree();break;
		case 8:a.KruskalMinTree();break;
		}
		if(command==7||command==8)
			cout << "输入指令(结束程序输入0）：";
		else
		{
			system("cls");
			printmenu(a);
		}
	}
}

SqList.h

#pragma once
#define MAXSIZE 100
#include
using namespace std;
typedef bool Status;
template <class T>
class SqList
{
private:
	T data[MAXSIZE];
	int length;//实际存放元素的个数
public:
	SqList();
	~SqList();
	Status Insert(int i, T e); //在i位置插入一个元素
	Status Delete(int i);//删除i位置的元素
	Status Update(int i, T e); //在i位置更新一个元素
	int Locate(T e);//根据元素查找在线性表中的位置
	T Output(int i);//返回值为第i个元素
};

Sqlist.cpp

#include "SqList.h"
#include
using namespace std;


template<class T>
SqList<T>::SqList()
{
	length = 0;
}

template<class T>
SqList<T>::~SqList()
{
}

template<class T>
Status SqList<T>::Delete(int i)
{
	if (length == 0)
		return false;
	if (i<1 || i>length)
		return false;
	T x = data[i];
	for (int j = i; j < length; j++)
		data[j] = data[j+1];
	length--;
    return true;
}

template<class T>
Status SqList<T>::Insert(int i, T x)
 {
	if (length >= MAXSIZE)
		return false;
	if (i<1 || i>length + 1)
		return false;
	for (int j = length; j >= i; j--)
		data[j+1] = data[j];
	data[i] = x;
	length++;
	return true;
 }

template<class T>
int SqList<T>::Locate(T x)
{
	int i;
	for (i = 1;i <= length;i++)
		if (data[i] == x)
			return i;
	return 0;
}

template<class T>
Status SqList<T>::Update(int i, T e)
{
	if (i <= length)
	{
		data[i] = e;
		return true;
	}
	else
	{
		return false;
	}
}

template<class T>
T SqList<T>::Output(int i)
{
	return data[i];
}

Graph.h

#pragma once
#define numMAX 20
#define StrMAX 100
#define MAX 100000
#include"SqList.h"
#include
using namespace std;

//顶点
struct Vex
{
	char Code[StrMAX];
	char Name[StrMAX];
	bool operator==(Vex rhs)
	{
		return(strcmp(Code, rhs.Code) == 0) && (strcmp(Name, rhs.Name) == 0);
	}
};
struct Edge
{
	Vex vex1;
	Vex vex2;
	int weight;
	bool operator==(Edge rhs)
	{
		return(strcmp(vex1.Code, rhs.vex1.Code) == 0) && (strcmp(vex2.Code, rhs.vex2.Code) == 0);
	}
};

class Graph
{
public:
	Graph();
	~Graph();
	bool InsertVex(Vex svex);
	bool DeleteVex(Vex svex);
	bool UpdateVex(Vex svex);
	bool UpdateEdge(Edge sedge);
	bool InsertEdge(Edge sedge);
	bool DeleteEdge(Edge sedge);
	void CreateUDN();

	Edge GetEdge(char *vex1Code, char *vex2Code);
	Vex GetVex(char *vex1Code);

	void PrimMinTree();//Prim最小生成树
	void KruskalMinTree();//Kruskal最小生成树
private:
	int AdjMatrix[numMAX][numMAX];//邻接矩阵
	SqList<Vex> Vexs;//顶点
	SqList<Edge> Edges;//边
	int Vexnum;//顶点数
	int Edgenum;//边数
	int num1,num2;
};

Prim 算法的实现与应用

假设 G=(V，E)是一个具有 n 个顶点的带权无向连通图，T(U，TE)是 G 的最小生成树，其
中 U 是 T 的顶点集，TE 是 T 的边集，则构造 G 的最小生成树 T 的步骤如下：
1）初始状态，TE 为空，U={v0}，v0∈V；
2）在所有 u∈U，v∈V-U 的边(u，v) ∈E 中找一条代价最小的边(u′，v′)并入 TE，同时将 v′并入 U；
重复执行步骤（2）n-1 次，直到 U=V 为止。

Kruskal 算法的实现与应用

假设 G=(V，E)是一个具有 n 个顶点的带权无向连通图，T(U，TE)是 G 的最小生成树，其
中 U 是 T 的顶点集，TE 是 T 的边集，则构造 G 的最小生成树 T 的步骤如下：
1）置 U 的初值等于 V，TE 的初值为空
2）将图 G 中的边按权值从小到大的顺序依次选取：若选取的边未使生成树 T 形成回路，
则加入 TE，否则舍弃，直到 TE 中包含（n-1）条边为止。

Graph.cpp

#include "Graph.h"
#include"SqList.h"
#include"SqList.cpp"
#include
#include
using namespace std;

Graph::Graph()
{
	Vexnum = 0;
	Edgenum = 0;
	int i;
	Vex vex1;
	Edge edge1;
	char a[StrMAX], b[StrMAX];
	cin >> num1 >> num2;
	for (i = 1;i <= num1;i++)
	{
		cout << "输入第" << i << "个点的名称：";
		cin >> vex1.Name;
		cout << "输入第" << i << "个点的代码：";
		cin>> vex1.Code;
		InsertVex(vex1);
	}
	for (i = 1;i <= num2;i++)
	{
		cout << "输入第" << i << "条边的两点代码：";
		cin >> a >> b;
		cout << "输入第" << i << "条边的长度：";
		cin	>> edge1.weight;
		edge1.vex1 = GetVex(a);
		edge1.vex2 = GetVex(b);
		InsertEdge(edge1);
	}
	cout << "初始化成功" << endl;
}

Graph::~Graph()
{
}

bool Graph::InsertVex(Vex svex)
{
	if (Vexs.Insert(++Vexnum, svex))
		return true;
	else
		return false;
}


bool Graph::InsertEdge(Edge sedge)
{
	if (Edges.Insert(++Edgenum, sedge))
		return true;
	else
	{
		return false;
	}
}

bool Graph::UpdateVex(Vex svex)
{
	cout << "请输入新点的代码和名称：";
	Vex a;
	cin >> a.Code;
	cin >> a.Name;
	if (DeleteVex(svex)&&InsertVex(a))
		return true;
	else
		return false;
}
bool Graph::DeleteVex(Vex svex)
{
	if (Vexs.Delete(Vexs.Locate(svex)))
	{
		Vexnum--;
		for (int i = 1; i <= Edgenum; i++)
			if (Edges.Output(i).vex1 == svex || Edges.Output(i).vex2 == svex)
				DeleteEdge(Edges.Output(i));
		return true;
	}
	else
	{
		return false;
	}
}
bool Graph::DeleteEdge(Edge sedge)
{
	if (Edges.Delete(Edges.Locate(sedge)))
	{
		Edgenum--;
		return true;
	}
	else
	{
		return false;
	}
}
bool Graph::UpdateEdge(Edge sedge)
{
	Edge a=sedge;
	cout << "请输入新边的长度：";
	cin >>a.weight;
	if (Edges.Update(Edges.Locate(sedge),a))
		return true;
	else
		return false;       
}

Edge Graph::GetEdge(char *vex1code,char *vex2code)
{
	int i = 1;
	while (true)
	{
		if ((strcmp(Edges.Output(i).vex1.Code , vex1code)==0&&strcmp(Edges.Output(i).vex2.Code,vex2code)==0)||(strcmp(Edges.Output(i).vex1.Code , vex2code)==0 &&strcmp(Edges.Output(i).vex2.Code,vex1code)==0))
			break;
		i++;
	}
	return Edges.Output(i);
}

Vex Graph::GetVex(char *vex1code)
{   int i = 1;
	while (true)
	{
		if (strcmp(Vexs.Output(i).Code,vex1code)==0)
		  break;
		i++;
	}
	return Vexs.Output(i);
}

void Graph::CreateUDN()
{
	int i, j;
	for (i = 1; i <= Vexnum; i++)
		for (j = 1; j <= Vexnum; j++)
			AdjMatrix[i][j] = MAX;
	for (i = 1; i <= Edgenum; i++)
	{
		AdjMatrix[Vexs.Locate(Edges.Output(i).vex1)][Vexs.Locate(Edges.Output(i).vex2)] = Edges.Output(i).weight;
		AdjMatrix[Vexs.Locate(Edges.Output(i).vex2)][Vexs.Locate(Edges.Output(i).vex1)] = Edges.Output(i).weight;
	}
	cout << "此时邻接矩阵" << endl<<"   ";
	for (i = 1; i <= Vexnum; i++)
		cout << Vexs.Output(i).Code<<" ";
	cout << endl;
	for (i = 1; i <= Vexnum; i++)
	{
		cout<<Vexs.Output(i).Code<<" ";
		for (j = 1; j <= Vexnum; j++)
		{
			if (AdjMatrix[i][j] == MAX)
			{
				cout<<"0  ";
			}
			else 
			{
				cout << AdjMatrix[i][j] << "  ";
			}
		}
		cout << endl;
	}//输出邻接矩阵
}
void Graph::PrimMinTree()
{
	cout << "请输入起始节点：";
	char code[StrMAX];
	cin >> code;
	cout << "prim最小生成树为：";
	int i, j,k,s;
	struct {
		char codes[StrMAX];
		int lowcost;
	}closedge[MAXSIZE];//设置一个辅助数组closedge，以记录U到V-U最小代价边
	k = Vexs.Locate(GetVex(code));
	for (j = 1;j <= Vexnum;j++)
	{
		if (j != k)
		{
			strcpy(closedge[j].codes,code);
			closedge[j].lowcost = AdjMatrix[k][j];
		}
	}//辅助数组初始化
	closedge[k].lowcost = 0;//初始，U={u}
	for (i = 1;i < Vexnum;i++)//选择其余vexnum-1个顶点
	{
		for (j = 1,s=MAX;j <= Vexnum;j++)
		{
			if ((s > closedge[j].lowcost)&&closedge[j].lowcost!=0)
			{
				s = closedge[j].lowcost;
				k = j;
			}
		}//k=最小lowcost所在的指针
		cout << closedge[k].codes << " "<< Vexs.Output(k).Code<<" "<<closedge[k].lowcost<<endl;
		closedge[k].lowcost = 0;
		for (j = 1;j <= Vexnum;j++)
			if ((AdjMatrix[k][j] < closedge[j].lowcost) && closedge[j].lowcost != 0)//新顶点并入U后重新选择最小边
			{
				strcpy(closedge[j].codes ,  Vexs.Output(k).Code );
				closedge[j].lowcost = AdjMatrix[k][j];
			}
	}
}

void Graph::KruskalMinTree()
{
	cout << "请输入起始节点：";
	char code[StrMAX];
	cin >> code;
	cout << "kruskal最小生成树为：";
	struct {
		char codes[StrMAX];
		int ad;
	}T[MAXSIZE];
	int i, j,s,k,x,y;
	for (i = 1;i <= Vexnum;i++)
	{
		strcmp(T[i].codes, Vexs.Output(i).Code);
		T[i].ad = i;
	}
	for (i = 1;i <= Edgenum;i++)
	{
		for (j = 1,s=MAX;j <= Edgenum;j++)
		{
			if (Edges.Output(j).weight < s&&(T[Vexs.Locate(Edges.Output(j).vex1)].ad!=T[Vexs.Locate(Edges.Output(j).vex2)].ad))
			{
				s = Edges.Output(j).weight;
				k = j;
			}
		}
		x = Vexs.Locate(Edges.Output(k).vex1);
		y = Vexs.Locate(Edges.Output(k).vex2);
		if (T[y].ad != T[x].ad)
		{
			cout << Edges.Output(k).vex1.Code << " " << Edges.Output(k).vex2.Code << " " << Edges.Output(k).weight << endl;
			for (j = 1;j <= Vexnum ;j++)
				if (T[j].ad == T[y].ad&& j != y)
					T[j].ad = T[x].ad;
			T[y].ad = T[x].ad;
		}
	}
}