图上寻找路径问题

图上寻找路径

今天开始介绍一种非常有用的算法，深度优先搜索算法。本片博文只是入门介绍一下。

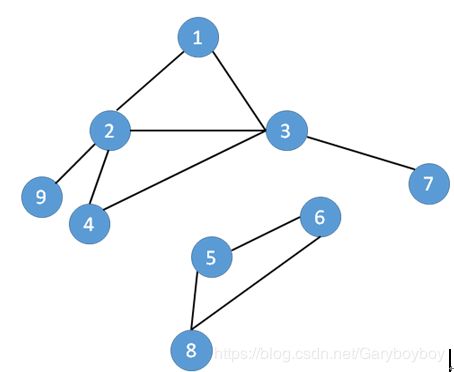
先提出问题，从1-8如何在图上寻找路径

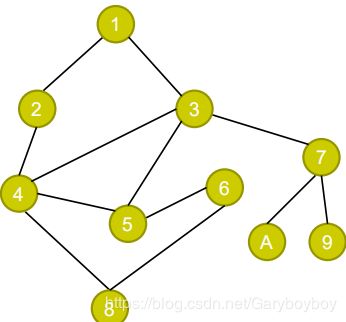
解决策略：
很简单，就是发现没走过的点就走过去。多个点可以走的时候，我们就随便选，无路可走就回退，然后再看看有没有没走过的点可以走

运气最差的时候就是走了1->3->7->9=>7->A=>7=>3->5->6->8

最好最走最左边那一条路

如果是不连通的路怎么办 遇到这种情况，你只有在走完全部的路径之后才会下结论说此路不通！

那么它大概的算法实现也是比较明了的了
下面讲解的全部都是伪代码

//判断从V出发是否能走到终点：
bool Dfs(V) { 
if( V 为终点）
	return true;
if( V 为旧点)   //前面找过的点，不管它行不行，这里我们都不管了，只走没走过的点
	return false;
	将V标记为旧点;  //其余情况就是V为新点
	对和V相邻的每个节点U { 
if( Dfs(U) == true)
	return true;
}
	return false; 
}

int main()
{
	将所有点都标记为新点;
	起点 = 1
	终点 = 8
	cout << Dfs(起点）; }

加多点要求：记录出路径出来

想必看完上面大家都感觉到其实我们把深度改成远度也是可以的了。
那么顾名思义，深度优先，我们用depth来来作为下标，把路径存在一维数组里面就大功告成了，稍微有一些细节处理一下就行。看伪代码：

Node path[MAX_LEN]; //MAX_LEN取节点总数即可，要什么数据类型自己决定
	int depth;
bool Dfs(V) {
if( V为终点）{
	path[depth] = V;
	return true;
}
if( V 为旧点)
	return false;
将V标记为旧点;
path[depth]=V;
++depth;
对和V相邻的每个节点U { 
if( Dfs(U) == true)
return true;
}
--depth;
return false;
}
int main()
{
将所有点都标记为新点;
depth = 0;
if( Dfs(起点）） {
for(int i = 0;i <= depth; ++ i)
cout << path[i] << endl;
}
 }

遍历这张图也不会有什么难度了

Dfs(V) {
if( V是旧点)
return;
将V标记为旧点;
对和V相邻的每个点 U {
Dfs(U);
} 
}
int main() {
将所有点都标记为新点;
while(在图中能找到新点k) 
Dfs(k);
}

遍历完上半部分节点，再下半部分

图的表示方法

一般情况下我们有两种表示的方法：

1. 邻接矩阵
2. 邻接表

两种有什么差异和作用在下面会给大家讲解

1.用一个二维数组G存放图，G[i][j]表示节点i和节点j之间边的情况(如有无边，边方向，权值大小等) 。

2.每个节点V对应一个一维数组(vector)，里面存放从V连出去的边，边的信息包括另一顶点，还可能包含边权值等。

当然还会有有向图
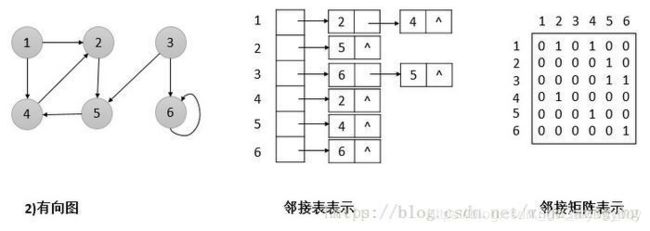1.如果G是一个无向图，那么所有邻接表的长度之和为2|E|，因为如果（u，v）是一条无向边，那么u会出现在v的邻接表中，v也会出现在u的邻接表中。

2.如果G是一个有向图，则对于边（u，v）中，节点v将会出现在u的邻接表里，因此，所有邻接链表的长度之等于|E|但不管是有向图还是无向图，邻接表需要的存储空间均为O（V+E）

3.对邻接表稍作变动，即可用来表示加权图，即每条边都有着相应权值的图，权值通常由加权函数w：E→R
给出。例如，设G=（V，E）是一个加权函数为w的加权图。对每一条边（u，v)∈E，权值w（u，v）和顶点v一起存储在u的邻接表中。

综上在所谓的稀疏的判断上，主要取决于n^2和e的比较

实现代码

邻接矩阵

#include
#include
#include
#include
#include
using namespace std;
int n,m,u,v,w,a[1000][1000];
int main(){
    scanf("%d%d",&n,&m);//给出n个点，m条边，要求建立邻接表存图
    for(int i=1;i<=m;i++){
        scanf("%d%d%d",&u,&v,&w);//表示u和v连了一条权值为w的边
        a[u][v]=a[v][u]=w;//无向边，表示u向v连了一条w的边，v也向w连了一条w的边
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            printf("%d",a[i][j]);
            //打印邻接矩阵,表示i向a[i][j]连了一条权值为val[i][j]的边
        }
        printf("\n");
    }
    //如果要找与节点x相连的边有哪些，x自己来定
    for(int i=1;i<=n;i++){
        if(a[x][i]>0){
            printf("%d %d %d\n",x,i,a[x][i]);
        }
    }
    return 0;
}

邻接表

#include
#include
#include
#include
#include
using namespace std;
int n,m,u,v,w,a[1000][1000],val[1000][1000],sum[1000];
int main(){
    scanf("%d%d",&n,&m);//给出n个点，m条边，要求建立邻接表存图
    for(int i=1;i<=m;i++){
        scanf("%d%d%d",&u,&v,&w);//表示u和v连了一条权值为w的边
        sum[u]++;a[u][sum[u]]=v;val[u][sum[u]]=w;
        sum[v]++;a[v][sum[v]]=w;val[v][sum[v]]=w;
        //无向边，表示u向v连了一条w的边，v也向w连了一条w的边
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=sum[i];j++){
            printf("%d %d %d\n",i,a[i][j],val[i][j]);
            //打印邻接表,表示i向a[i][j]连了一条权值为val[i][j]的边
        }
        printf("\n");
    }
    //如果要找与节点x相连的边有哪些
    for(int i=1;i<=sum[x];i++){
        printf("%d %d %d\n",x,a[x][i],val[x][i]);
    }
    return 0;
}

学会程序和算法，走遍天下都不怕

挪威盖朗厄尔峡湾
祝小伙伴们54青年节快乐！