获取程序运行时间以判别算法优劣

clock():捕捉从程序开始运行到clock()被调用所耗费的时间，这个时间单位是clock tick，即“时钟打点”。

常数CLK_TCK:机器时钟每秒所走的时间打点数

源代码示例：

#include 
#include 
clock_t start,stop;//clock_t是clock()函数返回的变量类型
double duration;//记录被测函数运行时间，以秒为单位 
int main()
{
	/*不在测试范围内的准备工作写在clock()之前*/
	start=clock();//开始计时 
	MyFunction();//把被测函数加在里面 
	stop=clock();//停止计时 
	duration=(double(stop-start))/CLK_TCK; //计算运行时间
	/*其他不在测试范围内的处理写在后面，例如输出duration的值*/ 
    return 0;
}

例如：计算下面式子的两个算法比较。

源代码：

#include 
#include 
#include 
clock_t start,stop;
double duration;
#define MAXN 10		//多项式项数，即多项式最大阶数加一 
double fun1(double a[],int n,double x);//n为数组最大下标 
double fun2(double a[],int n,double x);
int main()
{
	int i;
	double a[MAXN];	//存储系数
	for(i=0;i0;i--){
		result=a[i-1]+x*result;
	}
	return result;
}

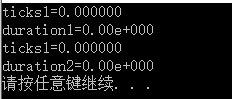
运行结果：

之所以结果都是0，这是因为程序跑得太快，捕捉时间太短。于是，可以利用重复多次运行程序方法进行比较。

修改代码如下：

#include 
#include 
#include 
clock_t start,stop;
double duration;
#define MAXK 1e7	//被测函数最大重复调用次数 
#define MAXN 10		//多项式项数，即多项式最大阶数加一 
double fun1(double a[],int n,double x);//n为数组最大下标 
double fun2(double a[],int n,double x);
int main()
{
	int i;
	double a[MAXN];	//存储系数
	for(i=0;i0;i--){
		result=a[i-1]+x*result;
	}
	return result;
}

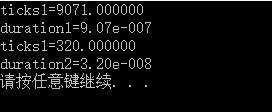
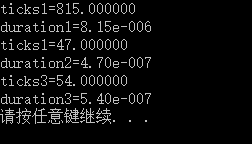
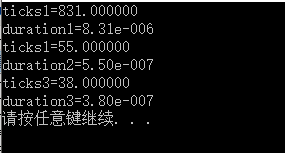
运行：

可见算法1的要比算法2大得多，算法2更好。

再如：

源代码：

#include 
#include 
#include 
clock_t start,stop;
double duration;
#define MAXK 1e5	//被测函数最大重复调用次数 
#define MAXN 101	//多项式项数，即多项式最大阶数加一 
double fun1(double x);
double fun2(double x);
int main()
{
	int i;
	start=clock();
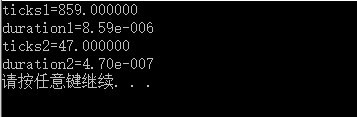
	for(i=0;i

注意，这里的最大重复调用次数是1e5

运行效果：

算法还是不够简洁，可以仿照上面的例子，利用数组初始化。

修改代码如下：

#include 
#include 
#include 
clock_t start,stop;
double duration;
#define MAXK 1e5	//被测函数最大重复调用次数 
#define MAXN 101	//多项式项数，即多项式最大阶数加一 
double fun1(double a[],int n,double x);
double fun2(double a[],int n,double x);
int main()
{
	int i;
	double a[MAXN];
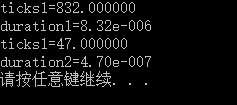
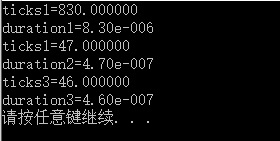
	for(i=1;i

效果：

额，仿佛也还是那回事。那再思考下，既然在第一个例子中“将f(x)看成f(x)=a0+x*(a1+x*(...(an-1+x*(an))...))”那么这道题也可以用同样的思想：

#include 
#include 
#include 
clock_t start,stop;
double duration;
#define MAXK 1e5	//被测函数最大重复调用次数 
#define MAXN 101	//多项式项数，即多项式最大阶数加一 
double fun1(double a[],int n,double x);
double fun2(double a[],int n,double x);
double fun3(double a[],int n,double x);
int main()
{
	int i;
	double a[MAXN];
	for(i=1;i1;i--){
		result=a[i-1]+x*result;
	}
	return result+1.0;
} 

跑了几次，感觉2和3差不多...

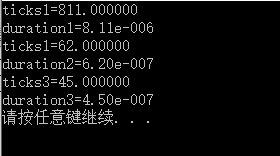
那就酱吧。