机器学习算法原理总结系列---算法基础之(2)决策树（Decision Tree）

一、原理详解

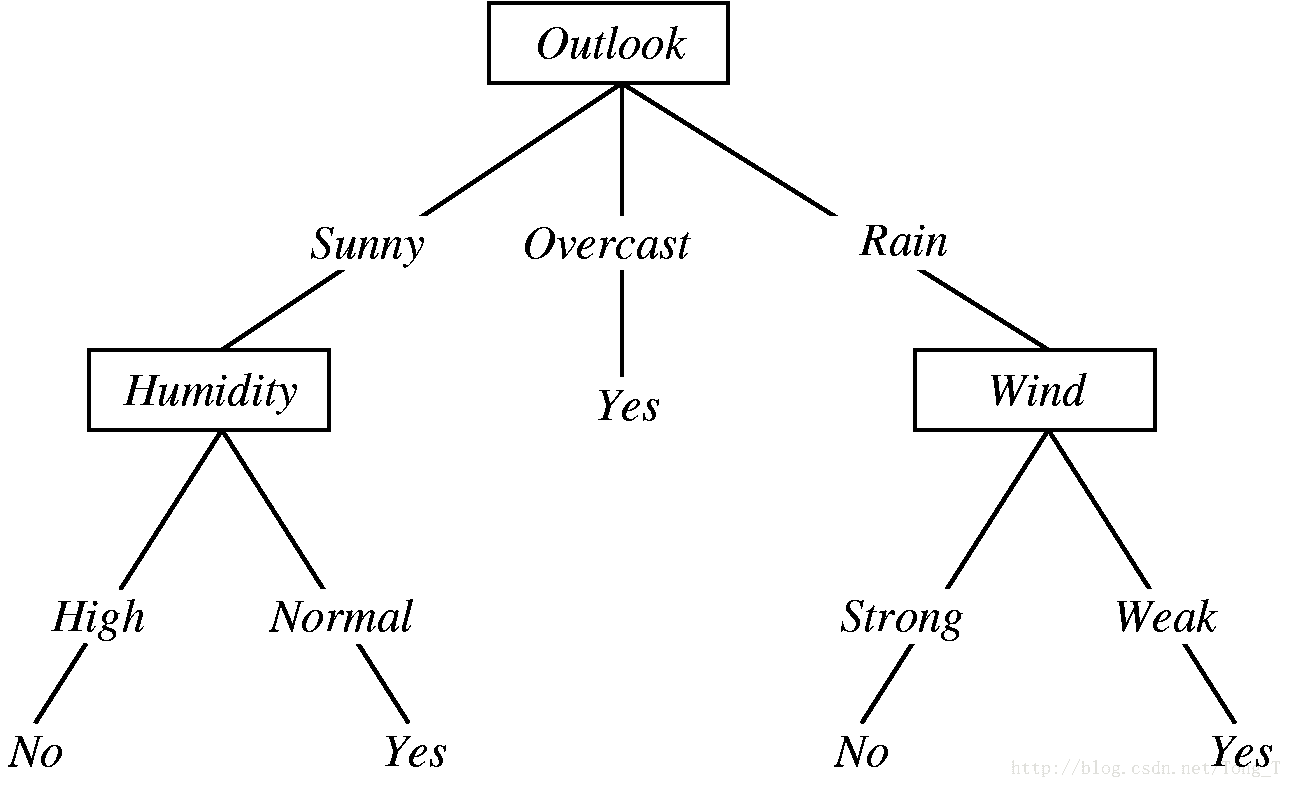
决策树是一个类似于流程图的树结构。其中，每个内部结点表示在一个属性上的测试，每个分支代表一个属性输出，而每个树叶结点代表类或类分布。树的最顶层是根结点。

机器学习中分类方法中的一个重要算法

构造决策树的基本算法：

1. 熵（entropy）的概念：
   信息和抽象，如何度量？
   1948年，香农提出了”信息熵(entropy)”的概念。
   一条信息的信息量大小和它的不确定性有直接的关系，要搞清楚一件非常非常不确定的事情，或者是我们一无所知的事情，需要了解大量信息==>信息量的度量就等于不确定性的多少

   比特(bit)来衡量信息的多少，信息的不确定性越大，熵也就越大；反过来说也是一样的，熵越大，信息的不确定性就越大。
   那到底是怎么度量的呢？数学家永远喜欢用一个等式表达他们的思想，计算熵的公式为：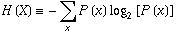

2. 决策树归纳算法 （ID3）
   根据entropy来确定的决策树算法其实也被叫做ID3算法。
   1970-1980， J.Ross. Quinlan, ID3算法

   选择属性判断结点

   信息获取量(Information Gain)：Gain(A) = Info(D) - Infor_A(D)
   通过A来作为节点分类获取了多少信息

   实战例子：
   
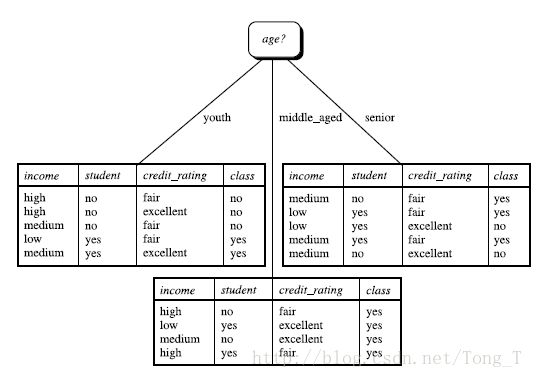
   任务：现在有14个人买电脑的实际数据，数据中体现的特征有每个人的年龄，收入，是否为学生，信用度。现在根据这些信息和属性来构建一个决策树，然后进行分类预测。再来一个人的话，可以有科学依据的进行预测到底买不买电脑。

   那么根据entropy来计算的过程是这样的：
   
   
   
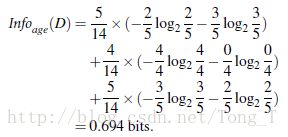
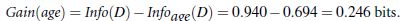
   类似，Gain(income) = 0.029, Gain(student) = 0.151, Gain(credit_rating)=0.048

   所以，选择age作为第一个根节点：
   

   然后重复这个求entropy的过程，接着继续去画分支，最后在终止条件下结束，也就画成了决策树。

3. 算法步骤归纳：

   1. 树以代表训练样本的单个结点开始（步骤1）。

   2. 如果样本都在同一个类，则该结点成为树叶，并用该类标号（步骤2 和3）。

   3. 否则，算法使用称为信息增益的基于熵的度量作为启发信息，选择能够最好地将样本分类的属性（步骤6）。该属性成为该结点的“测试”或“判定”属性（步骤7）。
   4. 在算法的该版本中，所有的属性都是分类的，即离散值。连续属性必须离散化。
   5. 对测试属性的每个已知的值，创建一个分枝，并据此划分样本（步骤8-10）。
   6. 算法使用同样的过程，递归地形成每个划分上的样本判定树。一旦一个属性出现在一个结点上，就不必该结点的任何后代上考虑它（步骤13）。
   7. 递归划分步骤仅当下列条件之一成立停止：
      (a) 给定结点的所有样本属于同一类（步骤2 和3）。
      (b) 没有剩余属性可以用来进一步划分样本（步骤4）。在此情况下，使用多数表决（步骤5）。这涉及将给定的结点转换成树叶，并用样本中的多数所在的类标记它。替换地，可以存放结点样本的类分布。
      (c) 分枝
      test_attribute = a i 没有样本（步骤11）。在这种情况下，以 samples 中的多数类创建一个树叶（步骤12）

其他算法：
- C4.5: Quinlan
- Classification and Regression Trees (CART): (L. Breiman, J. Friedman, R. Olshen, C. Stone)
共同点：都是贪心算法，自上而下(Top-down approach)
区别：属性选择度量方法不同： C4.5 gain ratio), CART(gini index), ID3 (Information Gain)

树剪枝叶 （避免overfitting)

• 先剪枝
• 后剪枝

决策树的优点：

• 直观，便于理解，小规模数据集有效

决策树的缺点：

• 处理连续变量不好
• 类别较多时，错误增加的比较快
• 可规模性一般

二、原生代码实现

任务同原理举得例子一样，这里放着全部的代码，笔者也不是全部是自己写的，但是每一行笔者都打印出来，看看实现的逻辑和结果。真心要想弄懂这些的话，100行代码也够你研究几个小时的了。

buy_computer.csv：

import csv
import operator
from math import log


def read_data():
    buy_computer = open('buy_computer.csv', 'r')
    reader = csv.reader(buy_computer)
    headers = next(reader)
    data_set = []
    for row in reader:
        # 删除将每一行的序号
        row.pop(0)
        data_set_item = []
        # 分别遍历每一行中的所有项，将其转换为数值
        for v in row:
            if v == 'youth':
                v = 0
            elif v == 'middle_aged':
                v = 1
            elif v == 'senior':
                v = 2
            elif v == 'low':
                v = 0
            elif v == 'medium':
                v = 1
            elif v == 'high':
                v = 2
            elif v == 'no':
                v = 0
            elif v == 'yes':
                v = 1
            elif v == 'fair':
                v = 0
            elif v == 'excellent':
                v = 1
            data_set_item.append(v)
        data_set.append(data_set_item)
    return headers[1:], data_set


def calculate_shan(data_set):
    """计算数据集的信息熵 （信息熵即指类别标签的混乱程度，值越小越好）"""
    data_set_length = len(data_set)
    p = {}
    H = 0.0
    for data in data_set:
        current_label = data[-1]  # 获取类别标签
        if current_label not in p.keys():  # 若字典中不存在该类别标签，即创建
            p[current_label] = 0
        p[current_label] += 1  # 递增类别标签的值
    for key in p:
        px = float(p[key]) / float(data_set_length)  # 计算某个标签的概率
        H -= px * log(px, 2)  # 计算信息熵
    return H


def spilt_data(data_set, axis, value):
    """
    根据某一特征分类数据集
    dataSet为要划分的数据集,axis为给定的特征，value为给定特征的具体值
    """
    sub_dataset = []
    for data in data_set:
        if data[axis] == value:
            sub_data = data[:axis]  # 取出data中第0到axis-1个数进subData;
            sub_data.extend(data[axis + 1:])  # 取出data中第axis+1到最后一个数进subData;这两行代码相当于把第axis个数从数据集中剔除掉
            sub_dataset.append(sub_data)  # 此处要注意expend和append的区别
    return sub_dataset


def choose_best_feature(data_set):
    """遍历所有特征，选择信息熵最小的特征，即为最好的分类特征"""
    len_feature = len(data_set[0]) - 1  # 计算特征维度时要把类别标签那一列去掉
    shan_init = calculate_shan(data_set)  # 计算原始数据集的信息熵
    init_value = 0.0
    best_feature = 0
    for i in range(len_feature):
        shan_carry = 0.0
        feature = [example[i] for example in data_set]  # 提取第i个特征的所有数据
        feature = set(feature)  # 得到第i个特征所有的分类值，如'0'和'1'
        for feat in feature:
            sub_data = spilt_data(data_set, i, feat)  # 先对数据集按照分类值分类
            prob = float(len(sub_data)) / float(len(data_set))
            shan_carry += prob * calculate_shan(sub_data)  # 计算第i个特征的信息熵
        out_value = shan_init - shan_carry  # 原始数据信息熵与循环中的信息熵的差
        if out_value > init_value:
            init_value = out_value  # 将信息熵与原始熵相减后的值赋给inValue，方便下一个循环的信息熵差值与其比较
            best_feature = i
    return best_feature


def majority_cnt(class_list):
    """选择列表中重复次数最多的一项"""
    class_count = {}
    for vote in class_list:
        if vote not in class_count.keys():
            class_count[vote] = 0
            class_count[vote] += 1
    sorted_class_count = sorted(class_count.items(),
                                key=operator.itemgetter(1),
                                reverse=True)  # 按逆序进行排列，并返回由元组组成元素的列表
    return sorted_class_count[0][0]


def create_tree(data_set, label):
    """创建我们所要分类的决策树"""
    class_list = [example[-1] for example in data_set]  # classList是指当前数据集的类别标签
    if class_list.count(class_list[0]) == len(class_list):  # 计算classList中某个类别标签的数量，若只有一类，则数量与它的数据长度相等
        return class_list[0]
    if len(data_set[0]) == 1:  # 当处理完所有特征而类别标签还不唯一时起作用
        return majority_cnt(class_list)
    feat_best = choose_best_feature(data_set)  # 选择最好的分类特征
    feature = [example[feat_best] for example in data_set]  # 接下来使用该分类特征进行分类
    feat_value = set(feature)  # 得到该特征所有的分类值，如'0'和'1'
    new_label = label[feat_best]
    del (label[feat_best])
    Tree = {new_label: {}}  # 创建一个多重字典，存储决策树分类结果
    for value in feat_value:
        sub_label = label[:]
        # 递归函数使得Tree不断创建分支，直到分类结束
        Tree[new_label][value] = create_tree(spilt_data(data_set, feat_best, value), sub_label)
    return Tree


headers, data_set = read_data()
tree = create_tree(data_set, headers)
print(tree)
'''
{
    'age': {
        0: {
            'student': {
                0: 0,
                1: 1
            }
        },
        1: 1,
        2: {
            'credit_rating': {
                0: 1,
                1: 0
            }
        }
    }
}
将数值变回原来的字符串形式为：
{
    'age': {
        'youth': {
            'student': {
                'no': 'no',
                'yes': 'yes'
            }
        },
        'middle_aged': 'yes',
        'senior': {
            'credit_rating': {
                'fair': 'yes',
                'excellent': 'no'
            }
        }
    }
}
'''

三、scikit-learn包实现

1. Python机器学习的库：scikit-learn
   1.1 特性：

   简单高效的数据挖掘和机器学习分析
   对所有用户开放，根据不同需求高度可重用性
   基于Numpy, SciPy和matplotlib
   开源，商用级别：获得 BSD许可

   2.2 覆盖问题领域：

   分类（classification), 回归（regression), 聚类（clustering), 降维(dimensionality reduction)

   模型选择(model selection), 预处理(preprocessing)

2. 使用用scikit-learn

   安装scikit-learn: pip
   安装必要package：numpy， SciPy和matplotlib， 可使用Anaconda (包含numpy, scipy等科学计算常用package）

   文档： http://scikit-learn.org/stable/modules/tree.html

3. 安装 Graphviz： http://www.graphviz.org/
   这是一个可视化的图形绘制工具软件，下载安装，然后配置环境变量。

   打开命令行终端：cd到文件目录：
   转化dot文件至pdf可视化决策树：dot -Tpdf buy_computer.dot -o output.pdf

 # 将dict类型的list数据，转换成numpy array
from sklearn.feature_extraction import DictVectorizer
import csv
from sklearn import preprocessing
from sklearn import tree
import numpy as np


class Data_Processing(object):
    def __init__(self):
        self.reader = None
        self.headers = None
        self.vec = None
        self.dummy_x = None
        self.dummy_y = None

    def read_data(self, path):
        buy_computer = open(path, 'r')
        self.reader = csv.reader(buy_computer)
        self.headers = next(self.reader)

    def pre_processing(self):
        feature_list = []
        label_list = []

        if self.reader and self.headers is None:
            raise ValueError

        for row in self.reader:
            label_list.append(row[len(row) - 1])
            row_dict = {}
            for i in range(1, len(row) - 1):
                row_dict[self.headers[i]] = row[i]
            feature_list.append(row_dict)

        # print("feature_list:" + str(feature_list))
        # print("label_list:" + str(label_list))

        self.vec = DictVectorizer()
        self.dummy_x = self.vec.fit_transform(feature_list).toarray()

        # print("dummy_x:" + str(dummy_x))
        print(self.vec.get_feature_names())

        lb = preprocessing.LabelBinarizer()
        self.dummy_y = lb.fit_transform(label_list)
        # print("dummy_y:" + str(dummy_y))


if __name__ == '__main__':
    dp = Data_Processing()
    dp.read_data('buy_computer.csv')
    dp.pre_processing()

    clf = tree.DecisionTreeClassifier(criterion='entropy')
    print(clf)
    clf_ = clf.fit(dp.dummy_x, dp.dummy_y)
    print("clf:" + str(clf_))

    with open('buy_computer.dot', 'w') as f:
        f = tree.export_graphviz(clf, feature_names=dp.vec.get_feature_names(), out_file=f)

    one_row_x = dp.dummy_x[0, :]
    print("one_row_x:" + str(one_row_x))
    new_row_x = one_row_x
    new_row_x[0] = 1
    new_row_x[2] = 0
    new_row_x = np.array(new_row_x).reshape((1, -1))
    print("new_row_x" + str(new_row_x))

    prediction_y = clf.predict(new_row_x)
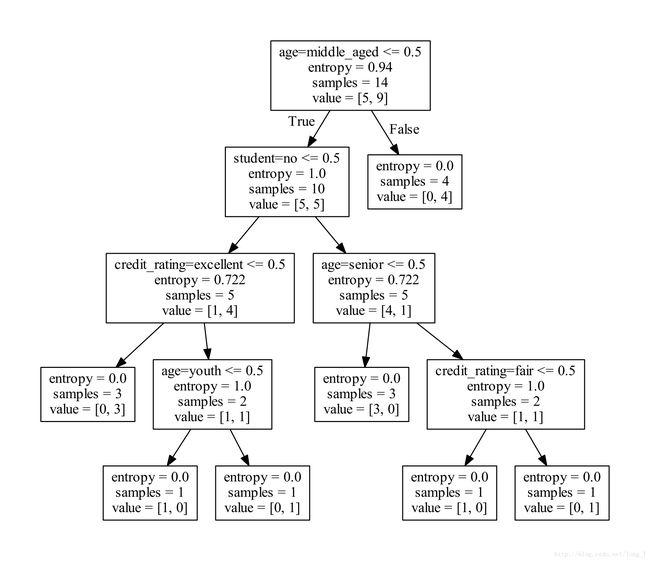
    print("prediction_y:" + str(prediction_y))

两种方式实现都能画出这样的图。有了这样的模型，我们就可以进行预测了。
上一组不同的数据来看看（上面代码中的这部分）：

    one_row_x = dp.dummy_x[0, :]
    print("one_row_x:" + str(one_row_x))
    new_row_x = one_row_x
    new_row_x[0] = 1
    new_row_x[2] = 0
    new_row_x = np.array(new_row_x).reshape((1, -1))
    print("new_row_x" + str(new_row_x))

    prediction_y = clf.predict(new_row_x)
    print("prediction_y:" + str(prediction_y))

从图中我们可以看出，新的一组数据，我们预测这个人是要买电脑。所以当模型的数据足够大，内容特征足够丰富影响做这个事儿的决断。我们就能很好的、很正确的进行预测。