路径规划Dijkstra算法
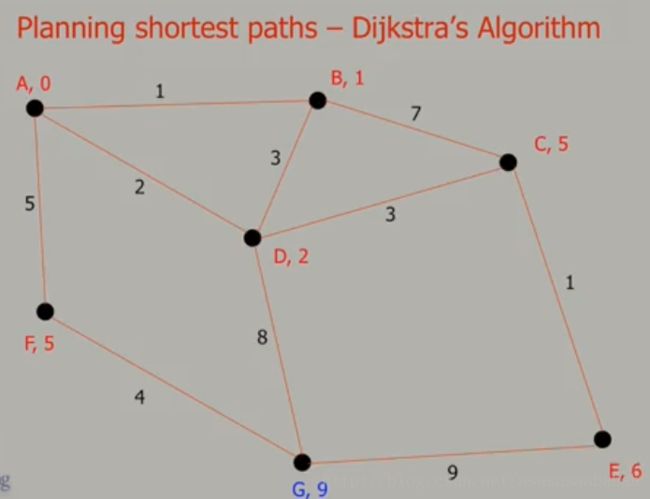
Dijkstra搜索最短路径:
整体思路
从起始节点开始,将邻域节点进行遍历,标注好邻域节点最小的累计路径长度,直到遍历到终止节点。
算法复杂度
- naive的方式,算法复杂度为 O(|V|2) ,其中 |V| 是节点数量
- 聪明的方式,使用优先队列,算法复杂度为 O((|E|+|V|)log(|V|)) ,其中 |E| 是边界数量, |V| 是节点数量。
伪代码
- 对所有图中的节点n
- n.distance = Infinity
- n.parent = nil
- 创建一个List。
- 起始节点start.distance = 0, start.parent = nil,将start节点放入List
- While(List 非空)
- 令current = List中distance最小的那个节点,然后将这个节点从List取出(表示这个节点已经完全访问过了,不需要以后在访问了)
- 对所有和current节点相邻的节点n
- tempDistance = current.distance + length of edge from n to current
- if(n.distance > tempDistance)
- n.distance = tempDistance;
- n.parent = current
- 如果整个过程还没有完成,那么就将n加入到list里边去(或者更新list里边n的distance值和parent值)。
Matlab代码
本节来自Cousera的Robotics课程
function [route,numExpanded] = DijkstraGrid (input_map, start_coords, dest_coords, drawMapEveryTime)
% Run Dijkstra's algorithm on a grid.
% Inputs :
% input_map : a logical array where the freespace cells are false or 0 and
% the obstacles are true or 1
% start_coords and dest_coords : Coordinates of the start and end cell
% respectively, the first entry is the row and the second the column.
% Output :
% route : An array containing the linear indices of the cells along the
% shortest route from start to dest or an empty array if there is no
% route. This is a single dimensional vector
% numExpanded: Remember to also return the total number of nodes
% expanded during your search. Do not count the goal node as an expanded node.
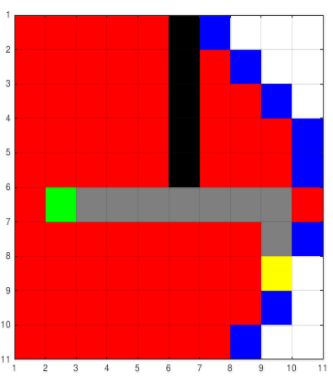
% set up color map for display
% 1 - white - clear cell
% 2 - black - obstacle
% 3 - red = visited
% 4 - blue - on list
% 5 - green - start
% 6 - yellow - destination
cmap = [1 1 1; ...
0 0 0; ...
1 0 0; ...
0 0 1; ...
0 1 0; ...
1 1 0; ...
0.5 0.5 0.5];
colormap(cmap);
% variable to control if the map is being visualized on every
% iteration
[nrows, ncols] = size(input_map);
% map - a table that keeps track of the state of each grid cell
map = zeros(nrows,ncols);
map(~input_map) = 1; % Mark free cells
map(input_map) = 2; % Mark obstacle cells
% Generate linear indices of start and dest nodes
start_node = sub2ind(size(map), start_coords(1), start_coords(2));
dest_node = sub2ind(size(map), dest_coords(1), dest_coords(2));
map(start_node) = 5;
map(dest_node) = 6;
% Initialize distance array
distanceFromStart = Inf(nrows,ncols);
% For each grid cell this array holds the index of its parent
parent = zeros(nrows,ncols);
distanceFromStart(start_node) = 0;
% keep track of number of nodes expanded
numExpanded = 0;
% Main Loop
while true
% Draw current map
map(start_node) = 5;
map(dest_node) = 6;
% make drawMapEveryTime = true if you want to see how the
% nodes are expanded on the grid.
if (drawMapEveryTime)
image(1.5, 1.5, map);
grid on;
axis image;
drawnow;
end
% Find the node with the minimum distance
[min_dist, current] = min(distanceFromStart(:));
if ((current == dest_node) || isinf(min_dist))
break;
end;
% Update map
map(current) = 3; % mark current node as visited
distanceFromStart(current) = Inf; % remove this node from further consideration
% Compute row, column coordinates of current node
[i, j] = ind2sub(size(distanceFromStart), current);
% *********************************************************************
% YOUR CODE BETWEEN THESE LINES OF STARS
% Visit each neighbor of the current node and update the map, distances
% and parent tables appropriately.
numExpanded = numExpanded + 1;
if(i-1>=1) %upper
id = sub2ind(size(map), i-1, j);
if((map(id) ~= 2) ... %if not obst
&& (map(id) ~= 3) ... % if not visited
&& (map(id) ~= 5)) ... % if not start
if(distanceFromStart(id) >= min_dist + 1)
distanceFromStart(id) = min_dist + 1;
parent(id) = current;
map(id) = 4;
end
end
end
if(i+1 <= nrows) %lower
id = sub2ind(size(map), i+1, j);
if((map(id) ~= 2) ... %if not obst
&& (map(id) ~= 3) ... % if not visited
&& (map(id) ~= 5)) ... % if not start
if(distanceFromStart(id) >= min_dist + 1)
distanceFromStart(id) = min_dist + 1;
parent(id) = current;
map(id) = 4;
end
end
end
if(j-1 >= 1) %left
id = sub2ind(size(map), i, j-1);
if((map(id) ~= 2) ... %if not obst
&& (map(id) ~= 3) ... % if not visited
&& (map(id) ~= 5)) ... % if not start
if(distanceFromStart(id) >= min_dist + 1)
distanceFromStart(id) = min_dist + 1;
parent(id) = current;
map(id) = 4;
end
end
end
if(j+1 <= ncols) %left
id = sub2ind(size(map), i, j+1);
if((map(id) ~= 2) ... %if not obst
&& (map(id) ~= 3) ... % if not visited
&& (map(id) ~= 5)) ... % if not start
if(distanceFromStart(id) >= min_dist + 1)
distanceFromStart(id) = min_dist + 1;
parent(id) = current;
map(id) = 4;
end
end
end
%*********************************************************************
end
%% Construct route from start to dest by following the parent links
if (isinf(distanceFromStart(dest_node)))
route = [];
else
route = [dest_node];
while (parent(route(1)) ~= 0)
route = [parent(route(1)), route];
end
% Snippet of code used to visualize the map and the path
for k = 2:length(route) - 1
map(route(k)) = 7;
pause(0.1);
image(1.5, 1.5, map);
grid on;
axis image;
end
end
end然后执行代码
map = false(10); %Input Map Parameters
map (1:5, 6) = true; %Obstacle Declaration
start_coords = [6, 2]; %Starting Coordinates
dest_coords = [8, 9]; %Destination Coordinates
drawMapEveryTime = false; %Display Outputs
[route, numExpanded] = DijkstraGrid(map,start_coords,dest_coords,drawMapEveryTime) %Implementation最终结果: