RegNet论文阅读笔记

1.解决问题

现有的配准方法中，雅可比矩阵的计算常常是采用数值计算，只利用了邻域的像素信息，使得优化对初始值的设定十分敏感。为了解决这一问题，这篇文章提出了一个基于两张图像特征图的雅可比矩阵学习网络，来增大收敛范围，增加配准网络的性能。

 

2.创新点

提出一个基于两张图像特征图的雅可比矩阵学习网络，增大收敛范围，增加准确度和鲁棒性。

3.重点

1.采用特征矩阵误差来代替光度误差，特征矩阵误差比光度误差更平滑，并且有更明显的最值，特征金字塔使得收敛范围更大。

2.深度预测网络中使用基础深度图的线性加权叠加形式联合训练得到最终的深度预测图，相比针对单个像素进行深度预测更容易。

3.雅可比矩阵采用学习网络得到，而不是通过数值计算得到，加大收敛范围。

4.整个网络采用“粗-精”的分层训练方式。利用最小化特征矩阵误差来估计转换矩阵，在重投影误差的限制下学习雅可比矩阵。

4.模型介绍

4.1整体流程介绍

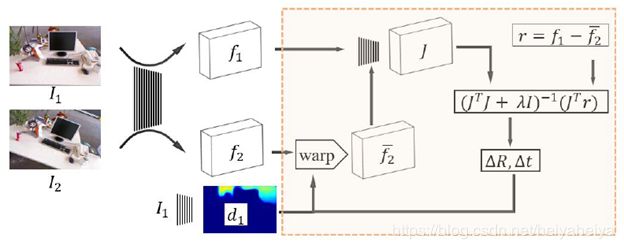
                                                    图1 整体流程图

由上图可知，在这篇文章中，输入两幅图像I1和I2,通过特征学习网络得到特征图f1,f2。F2与深度学习网络相连使用LM算法与相对姿态估计网络进行联合训练。这篇文章中采用特征矩阵误差来代替光度误差，特征矩阵误差比光度误差更平滑，并且有更明显的最值，特征金字塔使得收敛范围更大。深度预测网络中使用基础深度图的线性加权叠加形式联合训练得到最终的深度预测图，相比针对单个像素进行深度预测更容易。雅可比矩阵采用学习网络得到，而不是通过数值计算得到，加大收敛范围。

深度学习网络中使用权重向量w:   来预测深度基础图B，并表示深度图D。W通过最小化特征度量误差r 和转换矩阵T一起进行联合优化。

                                                                                                   (1)

                                                                                       (2)

公式(2)表示像素xi的特征度量误差，M是由图像分辨率决定的像素数。Xi代表图像I1中的像素坐标，通过函数  转换到I2空间。fk=F(Ik) ， k=0,1表示从图像 中学习到的特征表示。{w,T}通过最小化特征矩阵误差r的L2范式来实现：

                                                                                      (3)

式（3）通过LM算法进行优化计算：

                                                                                             （4）

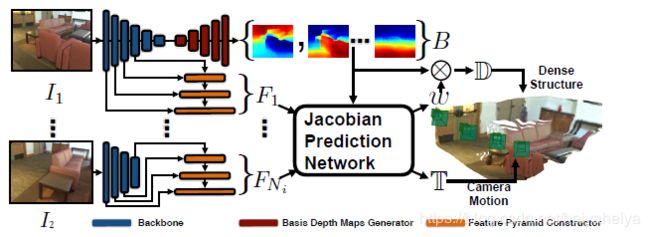
为了克服对于初始值敏感的问题，加大收敛范围，其中雅可比矩阵J通过连接特征图，和雅可比网络学习得到。深度预测网络和特征金字塔网络公用基础网络，整体网络框架图如下：

                                                           图2    网络架构图

 

4.2特征金字塔网络

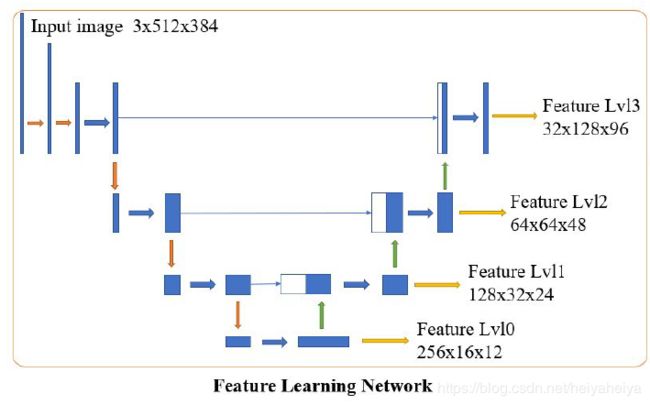
                                                                     图3    特征学习网络

使用类似U-Net的结构来预测不同分辨率下的特征图，使用卷积层提取特征，然后使用平均池化层进行下采样得到256维的16*12的L0层，来做初始配准。特征层使用双线性插值进行上采样，并在每个level上添加跳过连接进行扩展。这篇论文中，使用l0到l2的特征层进行粗略的配准，此时不需要对深度预测网络进行的优化。基于l2层进行初始姿势估计，特征层l3被用于准确配准以及深度预测图的优化。雅可比矩阵预测网络采用第一幅图像的特征图和第二幅图像的变换特征图进行输入，预测整个雅可比矩阵。

4.3雅可比矩阵学习网络

                                                                         图4   雅可比矩阵预测网络

相比于对特征矩阵进行数值雅可比矩阵计算，这篇文章对特征矩阵误差求偏导。并且由于对各个偏导数的可学习参数，有效的消除了特征表示上的平滑约束。在常用的数值计算迭代算法中，每一次迭代过程视为线性方程，整个过程是线性最小二乘法的叠加，通过对雅可比矩阵的学习，弥补了这一点。另外在神经网络中引入f1的信息，可以为雅可比矩阵添加更多约束，得到更稳健的结果。

 

4.4深度预测网络

使用U-Net作为编码器与特征金字塔共享特征。对于解码器，微调最后一层卷积到128通道，并使用这些特征图作为基础深度图进行优化。最后的深度图是基础深度图的线性组合【17】：

                                                                                            (5)

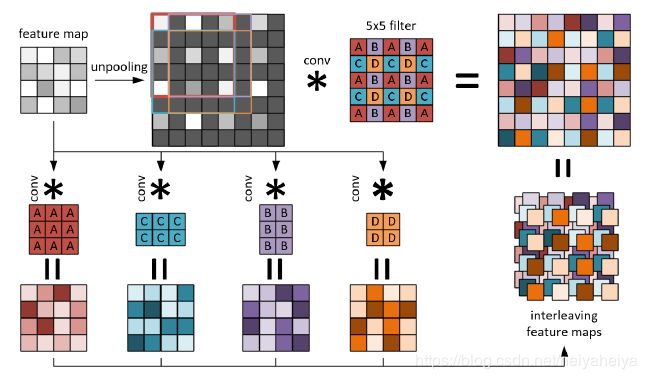
解码器中采用三个上采样层和一个卷积层，最后一个卷积层生成128个基础深度图，上采样层采用如下结构【18】，进行快速计算：

                                                                      图5    上采样层                   

4.5训练

采用分层的方式进行训练。首先，采用预训练的深度图作为初始值，仅预测l0层特征图，并与雅可比预测网络联合训练，用于优化。基于从上一层提供的初始相对变换，训练下一层来优化结果。对于雅可比预测网络，仅在第一层训练来进行初始化，后面的层使用数值雅可比行列式进行优化，因为初始值在收敛范围内。利用真实转换矩阵 和深度图 ，来最小化重投影误差：

                                                                     (6)

在最后一层中，联合训练特征提取网络和深度图预测网络：

                                                                            (7)

是指深度图之间的BerHu损失，D0是初始深度图，D1是优化的深度图，D* 是真实深度图，μ 是深度图损失和投影损失之间的比例常数。

5.不足

1.LM 算法中由于阻尼因子的存在，不可微，所以不能直接进行反向传递来训练特征学习网络。

2.只能处理刚性变换