2013年第四届蓝桥杯试题(Java本科B组)
1.标题: 世纪末的星期
曾有邪教称1999年12月31日是世界末日。当然该谣言已经不攻自破。
还有人称今后的某个世纪末的12月31日,如果是星期一则会....
有趣的是,任何一个世纪末的年份的12月31日都不可能是星期一!!
于是,“谣言制造商”又修改为星期日......
1999年的12月31日是星期五,请问:未来哪一个离我们最近的一个世纪末年(即xx99年)的12月31日正好是星期天(即星期日)?
请回答该年份(只写这个4位整数,不要写12月31等多余信息)
答案:2299
import java.util.Calendar;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
//Calendar的构造方式是protected,所以不能直接new
Calendar cal = Calendar.getInstance();
for (int i=2099; ; i+=100) {
//0表示1月,11表示12月
cal.set(i, 11, 31);
//星期日,星期一....对应对应1,2,3
if (cal.get(Calendar.DAY_OF_WEEK) == 1) {
System.out.println(i);
break;
}
}
}
}
3.标题: 振兴中华
小明参加了学校的趣味运动会,其中的一个项目是:跳格子。
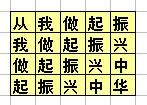
地上画着一些格子,每个格子里写一个字,如下所示:(也可参见p1.jpg)
从我做起振
我做起振兴
做起振兴中
起振兴中华
比赛时,先站在左上角的写着“从”字的格子里,可以横向或纵向跳到相邻的格子里,但不能跳到对角的格子或其它位置。一直要跳到“华”字结束。
要求跳过的路线刚好构成“从我做起振兴中华”这句话。
请你帮助小明算一算他一共有多少种可能的跳跃路线呢?
答案是一个整数,请通过浏览器直接提交该数字。
注意:不要提交解答过程,或其它辅助说明类的内容。
思路:随便找一条路从左上角走到右下角都能构成从我做起振兴中华这句话
答案:35
public class Main {
public static int[][] dir = { { 0, 1 }, { 1, 0 } };
public static int sum;
public static void main(String[] args) {
sum = 0;
dfs(0, 0);
System.out.println(sum);
}
private static void dfs(int x, int y) {
if (x == 3 && y == 4) {
sum++;
}
for (int i = 0; i < 2; i++) {
int newx = x + dir[i][0];
int newy = y + dir[i][1];
if (newx > 3 || newy > 4)
continue;
dfs(newx, newy);
}
}
}4.标题: 黄金连分数
黄金分割数0.61803... 是个无理数,这个常数十分重要,在许多工程问题中会出现。有时需要把这个数字求得很精确。
对于某些精密工程,常数的精度很重要。也许你听说过哈勃太空望远镜,它首次升空后就发现了一处人工加工错误,对那样一个庞然大物,其实只是镜面加工时有比头发丝还细许多倍的一处错误而已,却使它成了“近视眼”!!
言归正传,我们如何求得黄金分割数的尽可能精确的值呢?有许多方法。
比较简单的一种是用连分数:
1
黄金数 = ---------------------
1
1 + -----------------
1
1 + -------------
1
1 + ---------
1 + ...
这个连分数计算的“层数”越多,它的值越接近黄金分割数。
请你利用这一特性,求出黄金分割数的足够精确值,要求四舍五入到小数点后100位。
小数点后3位的值为:0.618
小数点后4位的值为:0.6180
小数点后5位的值为:0.61803
小数点后7位的值为:0.6180340
(注意尾部的0,不能忽略)
你的任务是:写出精确到小数点后100位精度的黄金分割值。
注意:尾数的四舍五入! 尾数是0也要保留!
显然答案是一个小数,其小数点后有100位数字,请通过浏览器直接提交该数字。
注意:不要提交解答过程,或其它辅助说明类的内容。
答案:0.6180339887498948482045868343656381177203091798057628621354486227052604628189024497072072041893911375
import java.math.BigDecimal;
public class Main {
public static void main(String[] args) {
BigDecimal one,sum;
one = sum = BigDecimal.ONE;
//具体的合适次数可以自己打印出来看
for (int i=0; i<1000; i++) {
sum = one.add(sum);
//设置精度和舍入方式
sum = one.divide(sum, 200, BigDecimal.ROUND_HALF_UP);
}
System.out.println(sum.setScale(100, BigDecimal.ROUND_HALF_UP));
}
}5.标题:有理数类
有理数就是可以表示为两个整数的比值的数字。一般情况下,我们用近似的小数表示。但有些时候,不允许出现误差,必须用两个整数来表示一个有理数。
这时,我们可以建立一个“有理数类”,下面的代码初步实现了这个目标。为了简明,它只提供了加法和乘法运算。
class Rational
{
private long ra;
private long rb;
private long gcd(long a, long b){
if(b==0) return a;
return gcd(b,a%b);
}
public Rational(long a, long b){
ra = a;
rb = b;
long k = gcd(ra,rb);
if(k>1){ //需要约分
ra /= k;
rb /= k;
}
}
// 加法
public Rational add(Rational x){
return ________________________________________; //填空位置
}
// 乘法
public Rational mul(Rational x){
return new Rational(ra*x.ra, rb*x.rb);
}
public String toString(){
if(rb==1) return "" + ra;
return ra + "/" + rb;
}
}
使用该类的示例:
Rational a = new Rational(1,3);
Rational b = new Rational(1,6);
Rational c = a.add(b);
System.out.println(a + "+" + b + "=" + c);
请分析代码逻辑,并推测划线处的代码,通过网页提交
注意:仅把缺少的代码作为答案,千万不要填写多余的代码、符号或说明文字!!
return new Rational(x.rb * ra + x.ra * rb,rb * x.rb);