数据结构与算法学习七:栈、数组模拟栈、单链表模拟栈、栈应用实例 实现 综合计算器
文章目录
- 前言
- 一、栈
- 1.1 栈的介绍
- 1.2 栈的应用实例【重点】
- 1.3 栈的应用场景
- 1.4 入栈与出栈
- 二、数据模拟栈
- 2.1 思路分析
- 2.2 代码结构
- 2.3 ArrayStack 栈类
- 2.4 ArrayStackMain 测试类
- 2.5 测试结果
- 三、单链表模拟栈
- 3.1 方法分析
- 3.2 代码结构
- 3.3 StackNode 链表节点
- 3.4 LinkedStack 栈方法
- 3.5 LinkedStackMain 测试方法
- 3.5 测试结果
- 四、栈+中缀表达式 实现综合计算器
- 4.1 需求描述
- 4.2 思路分析
- 4.3 代码实现
- 4.3.1 Calculator.java 计算类
- 4.3.2 ArrayStack.java 使用的栈(自定义,数组模拟栈)
前言
- 学习栈
- 了解栈的特点。
先进后出,后进先出。 - 使用数组模拟栈、链表模拟栈。(相比于双链表和单向环形链表来说是相对简单的)
- 栈的应用实例:
用栈+中缀表达式 实现综合计算器。 - 2020.4.21、22 日学习
- 相对于前面的双链表和单向环形链表,这里的数组模拟栈、链表模拟栈是比较简单的。
比较重要的是 栈的应用:栈+中缀表达式 实现综合计算器。关于中缀在下一节博客学习、讲解。
一、栈
1.1 栈的介绍
- 栈的英文为(stack)
- 栈是一个
先入后出(FILO-First In Last Out)的有序列表。 - 栈(stack)是限制线性表中元素的插入和删除
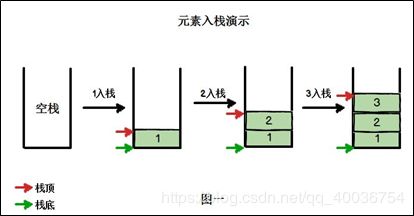
只能在线性表的同一端进行的一种特殊线性表。允许插入和删除的一端,为变化的一端,称为栈顶(Top),另一端为固定的一端,称为栈底(Bottom)。 - 根据栈的定义可知,最先放入栈中元素在栈底,最后放入的元素在栈顶,而删除元素刚好相反,最后放入的元素最先删除,最先放入的元素最后删除。
- 栈的基础方法为
入栈、出栈、显示栈数据。
1.2 栈的应用实例【重点】
请输入一个表达式
计算式:[722-5+1-5+3-3] 点击计算【如下图】
请问: 计算机底层是如何运算得到结果的? 注意不是简单的把算式列出运算,因为我们看这个算式 7 * 2 * 2 - 5, 但是计算机怎么理解这个算式的(对计算机而言,它接收到的就是一个 字符串 ),我们讨论的是这个问题。-> 栈
1.3 栈的应用场景
- 子程序的调用:在跳往子程序前,会先将下个指令的地址存到堆栈中,直到子程序执行完后再将地址取出,以回到原来的程序中。
- 处理递归调用:和子程序的调用类似,只是除了储存下一个指令的地址外,也将参数、区域变量等数据存入堆栈中。
- 表达式的转换:[中缀表达式转后缀表达式]与求值(实际解决)。
- 二叉树的遍历。
- 图形的深度优先(depth一first)搜索法。
1.4 入栈与出栈
二、数据模拟栈
2.1 思路分析
- 由于栈是一种有序列表,当然可以使用数组的结构来储存栈的数据内容,下面我们就用
数组模拟栈的出栈,入栈等操作 - 实现思路分析,并画出示意图
- 使用数组来模拟栈
定义一个 top 来表示栈顶,初始化 为 -1入栈的操作,当有数据加入到栈时,top++; stack[top] = data;出栈的操作,int value = stack[top]; top--, return value
2.2 代码结构
ArrayStack: 数组模拟栈的 类
ArrayStackMain:测试类

2.3 ArrayStack 栈类
package com.feng.ch06_stack.s1_arraystack;
/*
* 定义一个 ArrayStack 表示栈,数组模拟 栈
* */
public class ArrayStack {
private int maxSize; // 栈的大小
private int[] stack; // 数组,数组模拟栈,数据就放在数组中。
private int top = -1; // top 表示栈顶,初始化为-1
public ArrayStack(int maxSize) {
this.maxSize = maxSize;
this.stack = new int[this.maxSize];
}
//栈满
public boolean isFull(){
return top == maxSize-1;
}
// 栈空
public boolean isEmpty(){
return top == -1;
}
// 入栈
public void push(int value){
if (isFull()){
System.out.println("栈已满,无法添加~");
return;
}
top++;
stack[top] = value;
}
// 出栈,将栈顶的数据返回
public int pop(){
if (isEmpty()){
throw new RuntimeException("栈已空,无法获取数据\n");
}
int num = stack[top];
top--;
return num;
}
// 显示栈的情况【遍历栈】,遍历时,需要从栈顶开始显示数据
public void list(){
if (isEmpty()){
System.out.printf("栈空,无数据\n");
}
for (int i = top; i>=0; i--){
System.out.printf("stack[%d]=%d\n", i, stack[i]);
}
}
}
2.4 ArrayStackMain 测试类
package com.feng.ch06_stack.s1_arraystack;
import java.util.Scanner;
public abstract class ArrayStackMain {
public static void main(String[] args) {
// 测试 ArrayStack 是否正确
// 先创建一个 ArrayStack 对象 -》栈
ArrayStack stack = new ArrayStack(4);
String key = "";
boolean loop = true;
Scanner scanner = new Scanner(System.in);
while (loop) {
System.out.println("show:表示显示栈");
System.out.println("exit:退出程序");
System.out.println("push:表示添加数据到栈(入栈)");
System.out.println("pop:表示从栈取数据(出栈)");
System.out.println("请输入您的选择");
key = scanner.next();
switch (key) {
case "show":
stack.list();
break;
case "push":
System.out.println("请输入一个数:");
int value = scanner.nextInt();
stack.push(value);
break;
case "pop":
try {
int res = stack.pop();
System.out.printf("出栈的数据是 %d\n", res);
} catch (Exception e) {
System.out.println(e.getMessage());
}
break;
case "exit":
scanner.close();
loop = false;
break;
default:
break;
}
}
System.out.printf("程序退出成功~~~");
}
}
2.5 测试结果
三、单链表模拟栈
3.1 方法分析
栈的基础方法为入栈(push)、出栈(pop)、显示栈数据(list)
- 先创建头节点head。
- push():第一次添加时,直接添加到头结点的后面:
head.setNext(newNode);
第二次往后,先将头结点后面的节点挂载到newNode上,再将newNode挂载到head 上。即:
newNode.setNext(head.getNext());
head.setNext(newNode); - pop():直接输出头结点head后的一个节点即可,再将后一个节点的后一个节点挂载到 头节点即可:
StackNode next = head.getNext();
head.setNext(next.getNext());
return next; - list():设置辅助指针。循环遍历输出即可。
3.2 代码结构
StackNode: 链表节点
LinkedStack: 栈方法
LinkedStackMain: 测试方法
3.3 StackNode 链表节点
package com.feng.ch06_stack.s2_linkedstack;
public class StackNode {
private int no;
private StackNode next;
public StackNode(int no) {
this.no = no;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public StackNode getNext() {
return next;
}
public void setNext(StackNode next) {
this.next = next;
}
@Override
public String toString() {
return "StackNode{" +
"no=" + no +
'}';
}
}
3.4 LinkedStack 栈方法
package com.feng.ch06_stack.s2_linkedstack;
public class LinkedStack {
private StackNode head = new StackNode(0);
public StackNode getHead() {
return head;
}
/*
* 入栈
* */
public void push(StackNode newNode) {
if (head.getNext() == null) { // 第一次天机
head.setNext(newNode);
} else {
newNode.setNext(head.getNext());
head.setNext(newNode);
}
}
/*
* 出栈
* */
public StackNode pop(){
if (head.getNext() == null){
throw new RuntimeException("栈为空,无法出栈");
}
/*
* 两种返回方式
* */
// int value = head.getNext().getNo();
// head.setNext(head.getNext().getNext());
// return value;
StackNode next = head.getNext();
head.setNext(next.getNext());
return next;
}
/*
* 遍历
* */
public void list(){
if (head.getNext() == null){
System.out.println("栈为空,无法遍历");
return;
}
StackNode temporary = head.getNext();
while (true){
if (temporary == null){
break;
}
System.out.printf("节点编号%d\n",temporary.getNo());
temporary = temporary.getNext();
}
}
}
3.5 LinkedStackMain 测试方法
package com.feng.ch06_stack.s2_linkedstack;
public class LinkedStackMain {
public static void main(String[] args) {
LinkedStack stack = new LinkedStack();
StackNode node1 = new StackNode(1);
StackNode node2 = new StackNode(2);
StackNode node3 = new StackNode(3);
StackNode node4 = new StackNode(4);
StackNode node5 = new StackNode(5);
stack.push(node1);
stack.push(node2);
stack.push(node3);
stack.push(node4);
stack.push(node5);
System.out.println("初始化的栈:");
stack.list();
// 测试出栈
System.out.println();
System.out.println("出栈的数据:"+stack.pop());
System.out.println();
System.out.println("出栈后的栈:");
stack.list();
}
}
3.5 测试结果
四、栈+中缀表达式 实现综合计算器
4.1 需求描述
给定一个表达式字符串:【3+2*6-2】, 进行计算。
中缀表达式 就是 3+2*6-2 这种我们熟知的计算表达式。关于中缀表达式在下一节详细讲解
4.2 思路分析
- 使用上面开发的数组模拟栈,
新建两个栈,一个数栈、一个符号栈。 - 通过一个 index 值(索引),来遍历我们的表达式
- 如果我们
发现是一个数字, 就直接入数栈 - 如果发现
扫描到是一个符号, 就分如下情况
4.1 如果发现当前的符号栈为 空,就直接入栈
4.2 如果符号栈有操作符,就进行比较,如果 当前的操作符的优先级小于或者等于栈中的操作符, 就需要从数栈中pop出两个数,在从符号栈中pop出一个符号,进行运算,将得到结果,入数栈,然后将当前的操作符入符号栈,如果当前的操作符的优先级大于栈中的操作符, 就直接入符号栈。 - 当表达式扫描完毕,就顺序的从 数栈和符号栈中pop出相应的数和符号,并运行.
- 最后在数栈只有一个数字,就是表达式的结果
4.3 代码实现
- 先实现一位数的运算。
- 扩展到多位数的运算, 扩展多位的运算,主要改变的地方:
- 增加了一个变量
keepNum用户多位数的拼接, 然后在扫描时,遇到的字符 为数字时,再往后多看一位,如果是数字,则拼接,如果不是数组,则到此结束。
4.3.1 Calculator.java 计算类
package com.feng.ch06_stack.s3_calculator;
public class Calculator {
public static void main(String[] args) {
// 根据前面思路,完成表达式的运算
String expression = "3+2*6-2"; // 3+2*6-2=13
// 思考:如果处理多位数的问题? 30+2*6-2=40 。添加 keepNum 用于拼接多位数。
// 创建两个栈,数栈、一个符号栈
ArrayStack numStack = new ArrayStack(10);
ArrayStack operStack = new ArrayStack(10);
// 定义需要的相关变量
int index = 0; // 用于扫描
int num1 = 0;
int num2 = 0;
int oper = 0;
int res = 0;
char ch = ' '; // 将每次扫描得到插入保存到 ch
String keepNum = ""; // 用于拼接多位数
// 开始循环的扫描 expression
while (true) {
// 依次得到expression 的每一个字符
ch = expression.substring(index, index + 1).charAt(0);
/*
* 判断 ch 是什么,然后做相应的处理
* 如果是运算符
* */
if (operStack.isOperation(ch)) {
// 判断当前的符号栈是否为空
if (!operStack.isEmpty()) {
// 如果符号栈有操作符,就进行比较,如果当前的操作符的优先级小于或者等于栈中的操作符,就需要从数栈中 pop 出两个数,
// 在符号栈中 pop 出一个符号,进行运算,将得到结果,入数栈,然后将当前的操作符入符号栈。
if (operStack.priority(ch) <= operStack.priority(operStack.peek())) {
oper = operStack.pop();
num1 = numStack.pop();
num2 = numStack.pop();
res = numStack.calculation(num1, num2, oper);
// 把运算的结果入数栈
numStack.push(res);
// 然后把当前的操作符入符号栈
operStack.push(ch);
} else {
// 如果当前的操作符的优先级大于栈中的操作符,就直接入符号栈
operStack.push(ch);
}
} else {
// 如果为空,直接入栈。。
operStack.push(ch);
}
} else {// 如果是数
/*
* 如果是数,就直接入数栈, 这样不能满足 多位数。。。
* // ? "1+3" '1' => 1, ch 为字符,转换为 数字要 减48。
* 如果是个位数,用字符 char 来表示,则要减48,如果是多位数,下边变成了字符串,就直接使用包装类的方法转换成 整型
* */
//numStack.push(ch-48);
/*
* 解决多位数的 分析思路:
* 1、当处理多位数时,不能发现是一个数就立即入栈,因为他可能是多位数
* 2、在处理数时,需要向expression 的表达式的index 后在多看一位,如果是数就立刻扫描,如果是符号在入栈
* 3、因此定义一个 变量 字符串,用于拼接
* */
// 处理多位数
keepNum += ch;
// 如果 ch 已经是expression 的最后一位,就直接入栈
if (index == expression.length() - 1) {
numStack.push(Integer.parseInt(keepNum));
} else {
//判断下一个字符是不是数字,如果是数字,就继续扫描,如果是运算符,则入栈
// 注意是看后一位,不是 index++
if (operStack.isOperation(expression.substring(index + 1, index + 2).charAt(0))) {
// 如果后一位是运算符,则入栈, keepNum = "1" 或者 "123"
numStack.push(Integer.parseInt(keepNum));
keepNum = "";
}
}
}
// 让index +1 ,并判断 是否扫描到 expression 最后
index++;
if (index >= expression.length()) {
break;
}
}
/*
* 当表达式扫描完毕,就顺序的从数栈 和符号栈 中 pop 出相应的数和符号,并运行
* */
while (true) {
// 如果符号栈为空,则计算到最后的结果,数栈中只有一个数字【结果】
if (operStack.isEmpty()) {
break;
}
num1 = numStack.pop();
num2 = numStack.pop();
oper = operStack.pop();
res = numStack.calculation(num1, num2, oper);
numStack.push(res);
}
// 将数栈的最后数,pop出,就是结果
int result = numStack.pop();
System.out.printf("表达式 %s = %d", expression, result);
}
}
4.3.2 ArrayStack.java 使用的栈(自定义,数组模拟栈)
对于之前的数组模拟栈、链表模拟栈,这里需要增加几个方法:
peek(): 查看栈顶数据,但不是出栈。
priority(int oper):返回运算符的优先级,优先级是程序员来确定,优先级使用数字表示。
calculation(int num1, int num2, int oper):计算方法
package com.feng.ch06_stack.s3_calculator;
/*
* 先创建一个栈,直接使用前面创建好的,
* 需要扩展功能:增加
* 定义一个 ArrayStack 表示栈
* */
public class ArrayStack {
private int maxSize; // 栈的大小
private int[] stack; // 数组,数组模拟栈,数据就放在数组中。
private int top = -1; // top 表示栈顶,初始化为-1
public ArrayStack(int maxSize) {
this.maxSize = maxSize;
this.stack = new int[this.maxSize];
}
//栈满
public boolean isFull() {
return top == maxSize - 1;
}
// 栈空
public boolean isEmpty() {
return top == -1;
}
// 入栈
public void push(int value) {
if (isFull()) {
System.out.println("栈已满,无法添加~");
return;
}
top++;
stack[top] = value;
}
// 出栈,将栈顶的数据返回
public int pop() {
if (isEmpty()) {
throw new RuntimeException("栈已空,无法获取数据\n");
}
int num = stack[top];
top--;
return num;
}
// 显示栈的情况【遍历栈】,遍历时,需要从栈顶开始显示数据
public void list() {
if (isEmpty()) {
System.out.printf("栈空,无数据\n");
}
for (int i = top; i >= 0; i--) {
System.out.printf("stack[%d]=%d\n", i, stack[i]);
}
}
/*
* 查看栈顶的 数据, 不是真正出栈
* */
public int peek(){
return stack[top];
}
/*
* 返回运算符的优先级,优先级是程序员来确定,优先级使用数字表示
* 数字越大,则优先级越高。
* */
public int priority(int oper) {
if (oper == '*' || oper == '/') {
return 1;
} else if (oper == '+' || oper == '-') {
return 0;
} else {
return -1; // 假定目前的表达式只有 + - * /
}
}
/*
* 判断是不是一个云算法
* */
public boolean isOperation(char value) {
return value == '+' || value == '-' || value == '*' || value == '/';
}
/*
* 计算方法
* @param num1
* @param num2
* @param oper
* @return
* */
public int calculation(int num1, int num2, int oper){
int res = 0;
switch (oper){
case '+':
res = num1 + num2;
break;
case '-':
res = num2 - num1; // 注意顺序
break;
case '*':
res = num1 * num2;
break;
case '/':
res = num1/num2;
break;
default:
break;
}
return res;
}
}