九 哈希表、图、图的遍历
- 61.哈希表概述
- 62. 散列函数的设计
- 63.散列冲突的解决方案
- 64.图结构概述
- 65.图结构代码实现
- 66.图的遍历原理
- 67.图的遍历代码实现
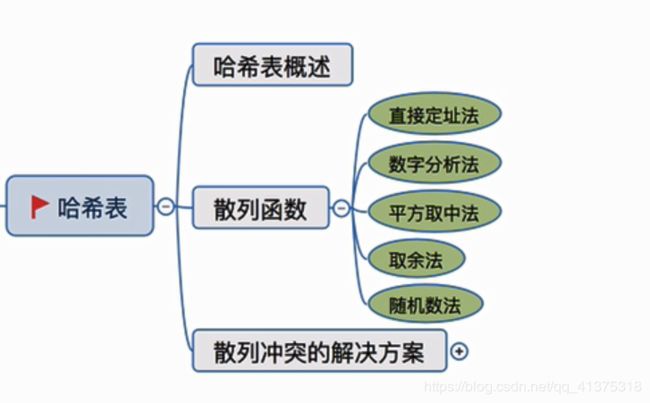
哈希(散列)表概述
散列表(Hash table,也叫哈希表),是根据关键码值(Key value)而直接进行访问的数据结构。也就是说,它通过把关键码值映射到表中一个位置来访问记录,以加快查找的速度。这个映射函数叫做散列函数,存放记录的数组叫做散列表。
给定表M,存在函数f(key),对任意给定的关键字值key,代入函数后若能得到包含该关键字的记录在表中的地址,则称表M为哈希(Hash)表,函数f(key)为哈希(Hash) 函数。
哈希表作为一种数据结构其实并不难,其本质就是一顺序存储的循序表。
只要牢牢抓住 M为哈希(Hash)表,函数f(key)为哈希(Hash) 函数 在代码中的实现就行

哈希表是顺序存储
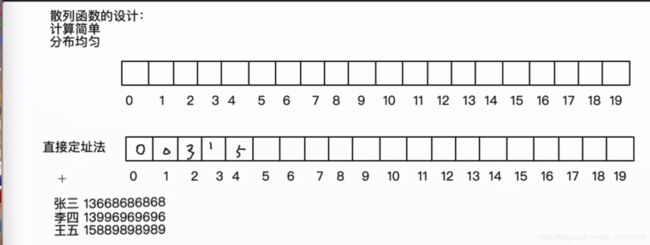
散列函数的设计
package demo13;
public class StuInfo {
private int age;
private int count;
public int getAge() {
return age;
}
public void setAge(int age) {
this.age = age;
}
public int getCount() {
return count;
}
public void setCount(int count) {
this.count = count;
}
/**
* 散列函数
*/
public int hashCode() {
return age;
}
public StuInfo(int age, int count) {
super();
this.age = age;
this.count = count;
}
public StuInfo(int age) {
super();
this.age = age;
}
@Override
public String toString() {
return "StuInfo [age=" + age + ", count=" + count + "]";
}
}
===================================================================================
package demo13;
import java.util.Arrays;
public class TestHashTable {
public static void main(String[] args) {
StuInfo s1 = new StuInfo(16, 3);
StuInfo s2 = new StuInfo(17, 11);
StuInfo s3 = new StuInfo(18, 23);
StuInfo s4 = new StuInfo(19, 24);
StuInfo s5 = new StuInfo(20, 9);
HashTable ht = new HashTable();
ht.put(s1);
ht.put(s2);
ht.put(s3);
ht.put(s4);
ht.put(s5);
System.out.println(ht);
//想要获取的目标数据
StuInfo target = new StuInfo(18);
StuInfo info = ht.get(target);
System.out.println(info);
}
}
===================================================================================
package demo13;
import java.util.Arrays;
public class HashTable {
private StuInfo[] data = new StuInfo[100];
/**
* 向散列表中添加元素
* @param stuInfo
*/
public void put(StuInfo stuInfo) {
//调用散列函数获取存储位置
int index = stuInfo.hashCode();
//添加元素
data[index]=stuInfo;
}
public StuInfo get(StuInfo stuInfo) {
return data[stuInfo.hashCode()];
}
@Override
public String toString() {
return "HashTable [data=" + Arrays.toString(data) + "]";
}
}
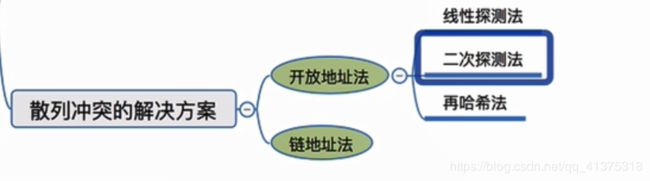
散列冲突的解决方案
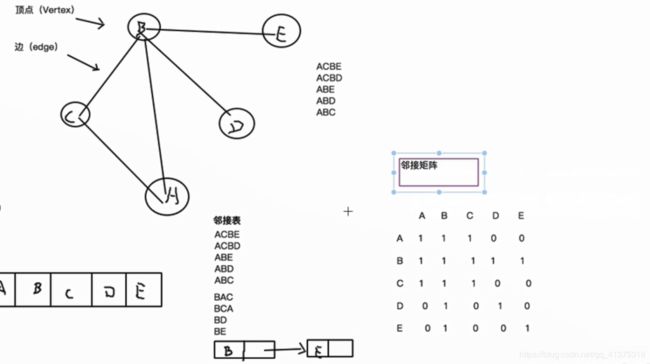
图结构概述
图虽然作为比较难的数据结构,但是如果能把握住图中主要含有的 顶点组 和 邻接矩阵就会容易理解和使用

图结构代码实现
public class Graph {
// 定义所有顶点
private Vertex[] vertex;
// 定义当前顶点多少
public int currentSize;
// 定义邻接矩阵
public int[][] adjMat;
// 图的构造函数,用于初始化
public Graph(int size){
vertex=new Vertex[size];
adjMat=new int[size][size];
}
// 加入顶点,就是加入顶点集合里
public void addVertex(Vertex v){
vertex[currentSize++]=v;
}
// 确定邻接矩阵,即确定边
public void addEdge(String v1,String v2) {
//找出两个顶点的下标
int index1=0;
int index2=0;
for(int i=0;i<vertex.length;i++){
if(vertex[i].getValue().equals(v1)){
index1=i;
break;
}
}
for(int i=0;i<vertex.length;i++){
if(vertex[i].getValue().equals(v2)){
index2=i;
break;
}
}
for(int i=0;i<vertex.length;i++){
adjMat[i][i]=1;
}
adjMat[index1][index2]=1;
adjMat[index2][index1]=1;
}
}
package demo14;
import demo2.MyStack;
/**
* 图
* @author Richard
*
*/
public class Graph {
private Vertex[] vertex;
private int currentSize;
public int[][] adjMat;
private MyStack stack = new MyStack();
//当前遍历的下标
private int currentIndex;
public Graph(int size) {
vertex=new Vertex[size];
adjMat=new int[size][size];
}
/**
* 向图中加入一个顶点
* @param v
*/
public void addVertex(Vertex v) {
vertex[currentSize++]=v;
}
public void addEdge(String v1,String v2) {
//找出两个顶点的下标
int index1=0;
for(int i=0;i<vertex.length;i++) {
if(vertex[i].getValue().equals(v1)) {
index1=i;
break;
}
}
int index2=0;
for(int i=0;i<vertex.length;i++) {
if(vertex[i].getValue().equals(v2)) {
index2=i;
break;
}
}
adjMat[index1][index2]=1;
adjMat[index2][index1]=1;
}
/**
* 深度优先搜索算法遍历图
*/
public void dfs() {
//把第0个顶点标记为已访问状态
vertex[0].visited=true;
//把第0个顶点的下标。
stack.push(0);
//打印顶点的值
System.out.println(vertex[0].getValue());
//遍历
out:while(!stack.isEmpty()) {
for(int i=currentIndex+1;i<vertex.length;i++) {
//如果和下一个遍历的元素是通的
if(adjMat[currentIndex][i]==1&&vertex[i].visited==false) {
//把下一个元素压入栈中
stack.push(i);
vertex[i].visited=true;
System.out.println(vertex[i].getValue());
continue out;
}
}
//弹出栈顶元素
stack.pop();
//修改当前位置为栈顶元素的位置
if(!stack.isEmpty()) {
currentIndex=stack.peek();
}
}
}
}
package demo14;
import java.util.Arrays;
public class TestGraph {
public static void main(String[] args) {
Vertex v1 = new Vertex("A");
Vertex v2 = new Vertex("B");
Vertex v3 = new Vertex("C");
Vertex v4 = new Vertex("D");
Vertex v5 = new Vertex("E");
Graph g = new Graph(5);
g.addVertex(v1);
g.addVertex(v2);
g.addVertex(v3);
g.addVertex(v4);
g.addVertex(v5);
//增加边
g.addEdge("A", "C");
g.addEdge("B", "C");
g.addEdge("A", "B");
g.addEdge("B", "D");
g.addEdge("B", "E");
for(int[] a:g.adjMat) {
System.out.println(Arrays.toString(a));
}
//深度优先遍历
g.dfs();
}
}
package demo14;
/**
* 顶点类
* @author Richard
*/
public class Vertex {
private String value;
public boolean visited;
public String getValue() {
return value;
}
public void setValue(String value) {
this.value = value;
}
public Vertex(String value) {
super();
this.value = value;
}
@Override
public String toString() {
return value;
}
}