重拾数据结构与算法(六)什么是二叉树
文章目录
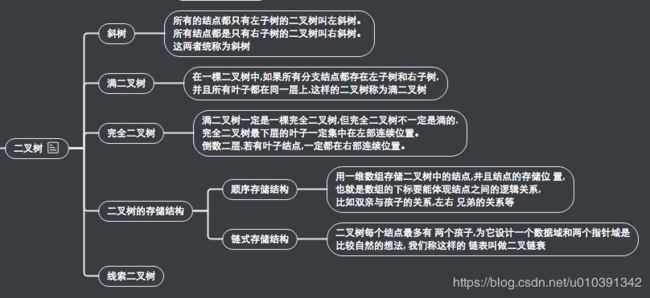
- 概述
- 二叉树五种基本形态
- 特殊二叉树
- 斜树
- 满二叉树
- 完全二叉树
- 二叉树的性质
- 二叉树的顺序存储结构
- 二叉树的链式存储结构
- 遍历二叉树
- 二叉树遍历方法
概述
二叉树是树的特殊一种,具有如下特点:
- 每个结点最多有两颗子树,结点的度最大为2。
- 左子树和右子树是有顺序的,次序不能颠倒。
- 即使某结点只有一个子树,也要区分左右子树。
二叉树五种基本形态
- 空二叉树。
- 只有一个根结点。
- 根结点只有左子树。
- 根结点只有右子树。
- 根结点既有左子树又有右子树。
特殊二叉树
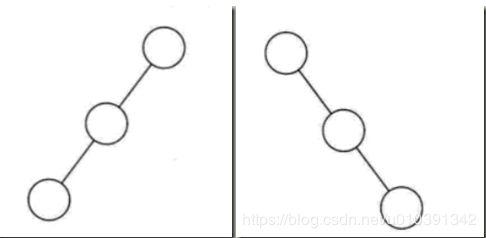
斜树
- 斜树一定要是斜的,但是往哪斜还是有讲究。所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树 。
- 斜树有很明显的特点,就是每 一层都只有一个结点,结点的个数与二叉树的深度相同 。
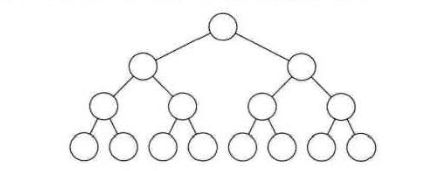
满二叉树
- 在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树
- 单是每个结点都存在左右子树,不能算是满二叉树,还必须要所有的叶子都在同一层上,这就做到了整棵树的平衡
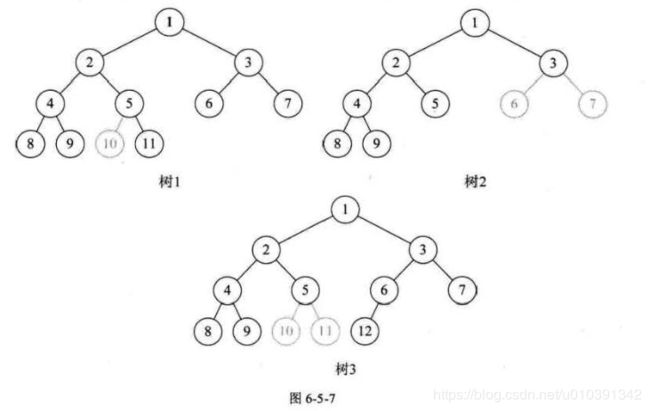
完全二叉树
- 对一棵具有n个结点的二叉树按层序编号,如果编号为
i的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树
满二叉树一定是一棵完全二叉树,但完全二叉树不一定是满的 。
完全二叉树的所有结点与同样深度的满二叉树,它们按层序编号相同的结点是一 一对应的
- 像图 6-5-7 中的树 1,因为5结点 没有左子树,却有右子树,那就使得按层序编号的第 10 个编号空档了。
- 同样道理,图 6-5-7 中的树2,由于3结点没有子树,所以使得 6、7 编号的位置空挡了。
- 图 6-5-7 中的树3又是因为5编号下没有子树造成第 10 和第 11 位置空档。
- 只有图 6-5-6 中的 树,尽管它不是满二叉树,但是编号是连续的,所以它是完全二叉树。
完全二叉树的特点:
- 叶子结点只能出现在最下两层。
- 最下层的叶子一定集中在左部连续位置。
- 倒数二层,若有叶子结点,一定都在右部连续位置。
- 如果结点度为 1,则该结点只有左孩子,即不存在只有右子树的情况。 同样结点数的二叉树,完全二叉树的深度最小。
二叉树的性质
-
在二叉树的第i层上至多有2的i-1次方个结点 (( 2 i − 1 2^i-1 2i−1))。
-
深度为k的二叉树至多有2的k次方减1个结点( 2 k − 1 2^k-1 2k−1)。
-
对任何一棵二叉树 T,如果其终端结点数为 n 0 n_0 n0,度为2的结点数为 n 2 n_2 n2,则 n 0 n_0 n0= n 2 n_2 n2+1
-
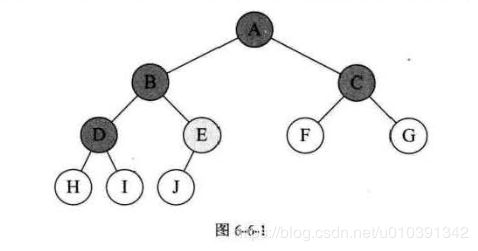
比如图 6-6-1 的例子,结点总数为 10,宫是由 A、 B、 c、 D 等度为 2 结点, F、 G、H、 l、J等度为0的叶子结点和E这个度为1的结点组成。 总和为4+1+5=10。
- 具有 n 个结点的完全二叉树的深度为[logn2n]+1
如果对一棵有 n 个结点的完全二叉树(其深度为 [logn2n]+1) 的结点按层 序编号(从第 1 层到第[logn2n]+1层,每层从左到右),对任一结点 i (1<=i<=n) 有:
- 如果
i=1,则结点 i 是二叉树的棍,无双亲;如果i> 1,则其双亲是结点 i 2 \frac{i}{2} 2i。 - 如果
2*i>n,则结点 i 左孩子(结点i为叶子结点) ;否则其左孩子是结点2*i。 - 如果
2*i+1>0,则结点i无右孩子;否则其右孩子是结点2*i+1.
- i=l 时就是根结点。 i>1 时,比如结点7的双亲就是7/2=3, 结点9它的双亲就是9/2=4
- 第二条, 比如结点 6,因为 2X6=12 超过了结点总数 10,所以结点 6 元左孩子 , 它是叶子结点。 同样,而结点5, 因为2XS=10正好是结点,总数10,所以它的左孩子 是结点 10。
- 第三条,比如结点 5,因为 2X5+1=l1,大于结点总数 10,所以它无右孩子。 而 结点 3,因为 2X3吐=7小于 10,所以宫的右孩子是结点 7
二叉树的顺序存储结构
- 二叉树的顺序存储结构就是用一维数组存储二叉树中的结点,井且结点的存储位
置,也就是数组的下标要能体现结点之间的逻辑关系,比如双亲与孩子的关系,左右 兄弟的关系等。 - 顺序存储 结构一般只用于完全二叉树。
package com.example.qxw.tree;
import java.util.Arrays;
/**
* 二叉树的顺序存储结构:
*
* 二叉树的顺序存储结构就是用一维数组存储二叉树中的结点,井且结点的存储位 置,
* 也就是数组的下标要能体现结点之间的逻辑关系,比如双亲与孩子的关系,左右 兄弟的关系等
*
* 顺序存储结构一般只用于完全二叉树
*
* @author qinxuewu
* @create 19/2/9下午6:12
* @since 1.0.0
*/
public class TreeTest01<T> {
//二叉树的默认深度
private final int DEFAULT_DEEP=16;
//二叉树的深度
private int k;
//用来存储数组的长
private int length;
//数据区域
private Object[] data;
//初始化二叉树
public TreeTest01(){
k=DEFAULT_DEEP;
//深度为k的二叉树至多有2的k次方减1个结点
length=(int) Math.pow(2, k);
data=new Object[length];
}
public TreeTest01(int deep){
this.k=deep;
length=(int) Math.pow(2, deep);
data=new Object[length];
}
//初始化二叉树 指定根结点
public TreeTest01(T element,int deep){
this.k=deep;
length=(int) Math.pow(2, deep);
data=new Object[length];
data[0]=element;
}
//根据元素查找在二叉树出现的第一个位置
public int indexOf(T element){
for(int i=0;i<data.length;i++){
if(data[i].equals(element)){
return i;
}
}
return -1;
}
//根节点
public T getRoot(){
return (T) data[0];
}
//
/**
* 查找指定结点的父节点
*
* 根据二叉树的性质:
* 如果i=1 ,则结点i是二叉树的根,无双亲;如果i> 1,则其双亲是结点(i/2)
* 所以得出求父节点公式:(index-1)/2 因为数据下标从0开始所以index-1。
*/
public T getParent(int index){
if(index==0){
throw new RuntimeException("该节点不存在父节点");
}
return (T) data[(index-1)/2];
}
//判断二叉树是否为空
public boolean isEmpty(){
return data[0]==null;
}
//获取指定结点
public T get(int index){
if(index>length||index<0){
throw new RuntimeException("超出底层数组范围");
}
return (T) data[index];
}
/**
* 为指定结点添加子节点
* @param index
* @param element
* @param left 是否是左结点
*/
public void add(int index,T element,boolean left){
if(data[index]==null){
throw new RuntimeException("该节点为空,不能添加子节点");
}
if(index*2+1>length||index*2+2>length){
throw new RuntimeException("超出底层数组范围");
}
if(left){
/**
* 根据二叉树的性质:
* 如果对一棵有 n 个结点的完全二叉树的结点按层序编号(每层从左到右))对任一结点i
* 如果 2*i>n(i=结点编号即下标 n=结点总数),则结点i无左孩子
* 所以得出data[index*2+1]下标处如果为空就不存在左子节点可以进行插入
*/
if(data[index*2+1]!=null){
throw new RuntimeException("该节点已经存在左子节点");
}else{
data[index*2+1]=element;
}
}else{
/**
* 根据二叉树的性质:
* 如果对一棵有 n 个结点的完全二叉树的结点按层序编号(每层从左到右))对任一结点i
* 如果 2*i+1>n(i=结点编号即下标 n=结点总数),则结点i无右孩子
* 所以得出data[index*2+1++]下标处如果为空就不存在右子节点可以进行插入
*/
if(data[index*2+2]!=null){
throw new RuntimeException("该节点已经存在右子节点");
}else{
data[index*2+2]=element;
}
}
}
//获取指定结点的右节点
public T getRight(int index){
if(index*2+1>length||index*2+2>length){
throw new RuntimeException("超出底层数组范围");
}
return (T) data[index*2+2];
}
//获取指定结点的左结点
public T getLeft(int index){
if(index*2+1>length||index*2+2>length){
throw new RuntimeException("超出底层数组范围");
}
return (T) data[index*2+1];
}
public String toString(){
if(data[0]==null){
return "[]";
}else{
return Arrays.toString(data);
}
}
public static void main(String[] args) {
//完全二叉树
TreeTest01<String> tree=new TreeTest01<>("A",4);
tree.add(0,"B",true); //左结点
tree.add(0,"C",false);//右结点
tree.add(1,"D",true);
tree.add(1,"E",false);
tree.add(2,"F",true);
tree.add(2,"G",false);
tree.add(3,"H",true);
tree.add(3,"I",false);
tree.add(4,"J",true);
System.out.println(tree.toString());
System.out.println(tree.get(2)); // 获取下标2的结点:C
System.out.println(tree.getParent(2));// 获取下标2的双亲结结点:A
System.out.println(tree.getRight(2));// 获取下标2的右子结点:G
System.out.println(tree.getLeft(2));// 获取下标2的左子结点:F
}
}
二叉树的链式存储结构
- 二叉树每个结点最多有 两个孩子,所以为它设计一个数据域和两个指针域是 比较自然的想法, 我们称这样的 链表叫做二叉链衰
data是数据区域。lchild和 民rchild都是指针域分别存放指向左孩子和右孩子的指针
遍历二叉树
- 二叉树的遍历是指从根结点出发,按照某种次序依次访问二叉树中所有结点.使得每个结点被访问-次 旦仅被访问一次 。
- 二叉树的遍历次序不同于线性结构,最多也就是从头至尾、循环、双向等简单的 遍历方式。树的结点之间不存在唯一的前驱和后继关系,在访问 一个结点后,下一个 被访问的结点面临着不同的选择 。
二叉树遍历方法
如果我们限制了从左到右的习惯方式,那么主要就分为四种
- 前序遍历
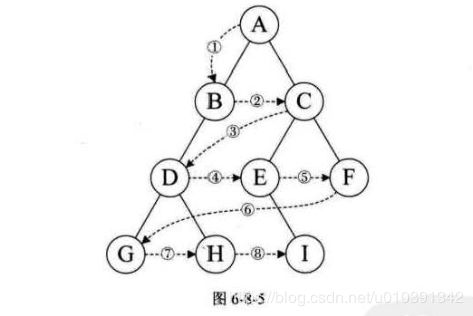
- 若二叉树为空,则空操作返回,否则先访问根结点,然后前序遍历左子 树 , 再前序遍历右子树
- 中序遍历
- 若树为空,则空操作返回,否则从根结点开始(注意并不是先访问根结点),中序遍历根结点的左子树,然后是访问根结点,最后中序遍历右子树 。
- 后序遍历
- 层序遍历
- 若树为空,则空操作返回,否则从树的第一层,也就是根结点开始访问, 从上而下逐层遍历,在同一层中, 按从左到右的颇用才结点逐个访问
public class TreeNode<E> {
private E data; //数据域
private TreeNode<E> lchild; //左孩子
private TreeNode<E> rchild; //右孩子
TreeNode(){}
TreeNode(E e){
this.data = e;
}
TreeNode(E data,TreeNode<E> lchild, TreeNode<E> rchild){
this.data = data;
this.lchild = lchild;
this.rchild = rchild;
}
public void setData(E data){
this.data = data;
}
public E getData(){
return this.data;
}
public void setLchild(TreeNode<E> lchild){
this.lchild = lchild;
}
public TreeNode<E> getLchild(){
return this.lchild;
}
public void setRchild(TreeNode<E> rchild){
this.rchild = rchild;
}
public TreeNode<E> getRchild(){
return this.rchild;
}
}
public class BinaryTree<E> {
private TreeNode<E> root; //根节点
private List<TreeNode> nodeList = null; //二叉树节点的链式结构
public BinaryTree(){
}
public BinaryTree(TreeNode<E> root){
this.root = root;
}
//把一个数组转化为一颗完全二叉树
public TreeNode<E> buildTree(E[] array){
nodeList = new LinkedList<TreeNode>();
//将数组中的元素依次转换为TreeNode节点,存放于链表中
for(int i=0; i< array.length; i++){
nodeList.add(new TreeNode(array[i]));
}
//对前(array.length / 2 - 1)个父节点,按照父节点与孩子节点的数字关系建立完全二叉树
for(int j=0; j < (array.length/2-1);j++){
/**
* 根据二叉树的性质:
* 如果对一棵有 n 个结点的完全二叉树的结点按层序编号(每层从左到右))对任一结点i
* 如果 2*i>n(i=结点编号即下标 n=结点总数),则结点i无左孩子
* 如果 2*i+1>n(i=结点编号即下标 n=结点总数),则结点i无右孩子
*/
//左孩子 (2*i+1)
nodeList.get(j).setLchild(nodeList.get(j*2+1));
//右孩子 2*i+2)
nodeList.get(j).setRchild(nodeList.get(j*2+2));
}
//最后一个父节点:因为最后一个父节点可能没有右孩子,所以单独处理
int index = array.length/2 -1;
//左孩子
nodeList.get(index).setLchild(nodeList.get(index*2+1));
//右孩子:如果数组的长度为奇数才有右孩子
if(array.length % 2 == 1){
nodeList.get(index).setRchild(nodeList.get(index*2+2));
}
root=nodeList.get(0); //设置根节点
return root;
}
//得到树的高度
public int height(TreeNode<E> node){
if(node == null){
return 0;
}else{
int i = height(node.getLchild());
int j = height(node.getRchild());
return (i<j)?(j+1):(i+1);
}
}
//递归计算节点的总个数
public int size(TreeNode<E> node){
if(node == null){
return 0;
}else{
//根节点+左子节点+右子节点
return 1+ size(node.getLchild())+size(node.getRchild());
}
}
/**
* 递归实现先序遍历
* 先访问根结点,然后前序遍历左子 树 , 再前序遍历右子树
* @param node
*/
public void preOrder(TreeNode<E> node){
if(node != null){
System.out.print(node.getData() + " ");
preOrder(node.getLchild());
preOrder(node.getRchild());
}
}
/**
* 递归实现中序遍历
* 从根结点开始(注意并不是先访问根结点),中序遍历根结点的左子树,
* 然后是访问根结点,最后中序遍历右子树
* @param node
*/
public void inOrder(TreeNode<E> node){
if(node != null){
inOrder(node.getLchild());
System.out.print(node.getData() + " ");
inOrder(node.getRchild());
}
}
/**
* 递归实现后序遍历
* 从左到右先叶子后结点的方式遍历访问左右子树,最后是访问根结点
* @param node
*/
public void postOrder(TreeNode<E> node){
if(node != null){
postOrder(node.getLchild());
postOrder(node.getRchild());
System.out.print(node.getData() + " ");
}
}
/**
* 层序遍历
*
* 从树的第一层,也就是根结点开始访问, 从上而下逐层遍历,
* 在同一层中, 按从左到右的颇用才结点逐个访问
* @param root
*/
public void levelOrder(TreeNode<E> root){
Queue<TreeNode<E>> nodeQueue = new LinkedList<TreeNode<E>>();
TreeNode<E> node = null;
nodeQueue.add(root); //将根节点入队
while(!nodeQueue.isEmpty()){ //队列不空循环
node = nodeQueue.peek();
System.out.print(node.getData()+" ");
nodeQueue.poll(); //队头元素出队
if(node.getLchild() != null){ //左子树不空,则左子树入队列
nodeQueue.add(node.getLchild());
}
if(node.getRchild() != null){ //右子树不空,则右子树入队列
nodeQueue.add(node.getRchild());
}
}
}
public static void main(String[] args) {
//将一个数组转化为一颗完全二叉树
//将一个数组转化为一颗完全二叉树
Object[] array = {1,2,3,4,5,6,7,8};
BinaryTree bt = new BinaryTree();
TreeNode root = bt.buildTree(array);
System.out.println("height: "+bt.height(root));
System.out.println("size: "+bt.size(root));
System.out.println("先序遍历:");
bt.preOrder(root);
System.out.println();
System.out.println("中序遍历:");
bt.inOrder(root);
System.out.println();
System.out.println("中序遍历:");
bt.levelOrder(root);
System.out.println();
System.out.println("层次遍历:");
bt.levelOrder(root);
}
}
*《大话数据结构》
- 参考:https://www.cnblogs.com/CherishFX/p/4617105.html
- 面试常见二叉树算法题 https://blog.csdn.net/u012428012/article/details/79089915