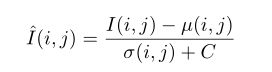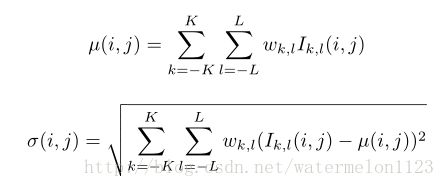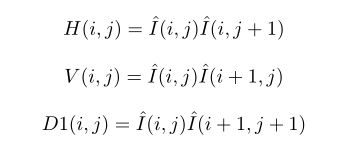图像质量评估BRISQUE算法详解
BRISQUE算法来源于论文:《No-Reference Image Quality Assessment in the Spatial Domain》
BRISQUE的意思是Blind/Referenceless Image Spatial QUality Evaluator,一种无参考的空间域图像质量评估算法。算法总体原理就是从图像中提取mean subtracted contrast normalized (MSCN) coefficients,将MSCN系数拟合成asymmetric generalized Gaussian distribution(AGGD)非对称性广义高斯分布,提取拟合的高斯分布的特征,输入到支持向量机SVM中做回归,从而得到图像质量的评估结果。
MSCN系数
MSCN系数I(x,y)定义
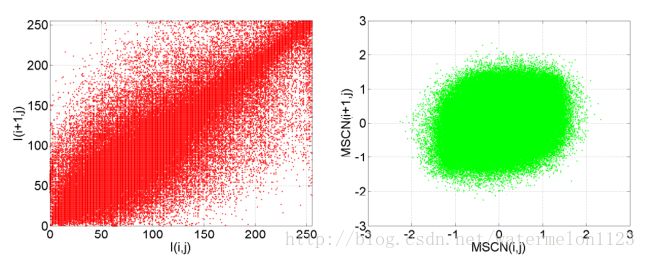
其中u(x,y)为高斯滤波后的结果,σ(x,y)为标准差。MSCN系数的优点在于因为纹理等特征而产生的区域corelation很小。如下图左侧(原始像素点)和右侧(MSCN)结果间的区别。
在图像中体现出的效果如下,右下角为MSCN系数结果:
可以看出MSCN对于纹理的强弱并没有非常强的依赖性,这样提取出来的特征更有适用性。
拟合成GGD
广义高斯分布GGD的定义:
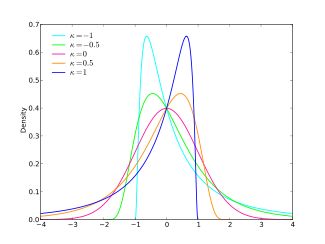
计算过程不详细说。有两点需要注意,GGD的特点在其模型可以发现数据的非正常分布,比如:
因为数据的特殊分布会产生左倾斜和右倾斜的现象。在图像质量评估中,因为各种distortion的影响,都会导致GGD分布的变形,比如:
可以看到不同的distortion对分布结果产生的影响。
Four orientation
为了加入相连像素间的关联信息,BRISQUE在计算的时候选取了4个方向分别计算MSCN。
即当前像素与下方,右方,主、次对角线4个方向分别进行计算。
拟合成AGGD
非对称性广义高斯分布asymmetric generalized Gaussian distribution(AGGD),定义如下:
计算过程不详说,AGGD主要是为了更好的拟合distortion image产生的非对称高斯分布,例如:
因为不同的distortion会使得AGGD产生不同的左右非对称现象,AGGD的pair parameters能更好的拟合出这种现象。
Two-stagePerformance
这一步主要是通过对原图和0.5倍原图大小的图像分别提取上述特征,能产生更好的效果。
综上所述,通过GGD输出2个feature,四个方向AGGD输出4*4=16个feature,再经过twostage,每幅图像共输出2*(2+4*4)=36个feature,将这些feature输入到SVM中做回归即可得到图像distortion的结果。作者的SVM模型是基于TID数据库进行训练的。
作者给出了开源matlab/c++源码:
http://live.ece.utexas.edu/research/quality/
代码需要林智仁教授的libsvm支持:
https://www.csie.ntu.edu.tw/~cjlin/libsvm/index.html
注意因为作者使用的libsvm版本貌似和最新的3.2版本libsvm冲突,所以建议使用3.1版本的libsvm。使用方法非常简单,可以自己写一个脚本做测试:
img=imread('testimage1.bmp');
qualityscore=brisquescore(img);
得到的qualityscore为图像质量结果,注意因为用svm作回归,qualityscore的结果越高代表图像质量越差。
对于输出feature的部分代码我做了些注释,仅供参考。
function feat = brisque_feature(imdist)
%------------------------------------------------
% Feature Computation
%-------------------------------------------------
scalenum = 2;
window = fspecial('gaussian',7,7/6); %创建7*7的高斯滤波器,标准差为7/6
window = window/sum(sum(window));
feat = [];
tic %tic和toc记录matlab命令执行的时间
%循环两次,two-stage framework?
for itr_scale = 1:scalenum
mu = filter2(window, imdist, 'same'); %用window对imdist进行滤波
mu_sq = mu.*mu;
sigma = sqrt(abs(filter2(window, imdist.*imdist, 'same') - mu_sq));
structdis = (imdist-mu)./(sigma+1); %论文中公式(1),计算?I(i,j)
[alpha overallstd] = estimateggdparam(structdis(:)); %计算zero mean GGD,得到GGD (α, σ ^2 )
feat = [feat alpha overallstd^2];
shifts = [ 0 1;1 0 ; 1 1; -1 1];
for itr_shift =1:4
shifted_structdis = circshift(structdis,shifts(itr_shift,:)); %循环位移
pair = structdis(:).*shifted_structdis(:);
[alpha leftstd rightstd] = estimateaggdparam(pair);
const =(sqrt(gamma(1/alpha))/sqrt(gamma(3/alpha)));
meanparam =(rightstd-leftstd)*(gamma(2/alpha)/gamma(1/alpha))*const; %公式15
feat =[feat alpha meanparam leftstd^2 rightstd^2]; %对照TABLE 1
end
%feat为最终输出的特征feature 一共含有18项
imdist = imresize(imdist,0.5);
end
toc