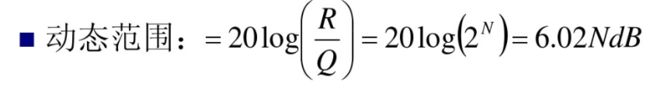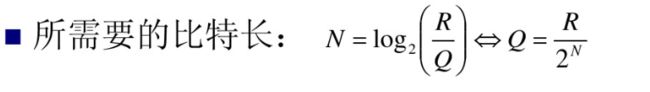一、数字信号处理概述
1.数字信号
(1)信号:信号是运载信息的载体,没有信息,信号将毫无意义
(2)数字信号:用计算机处理的信号
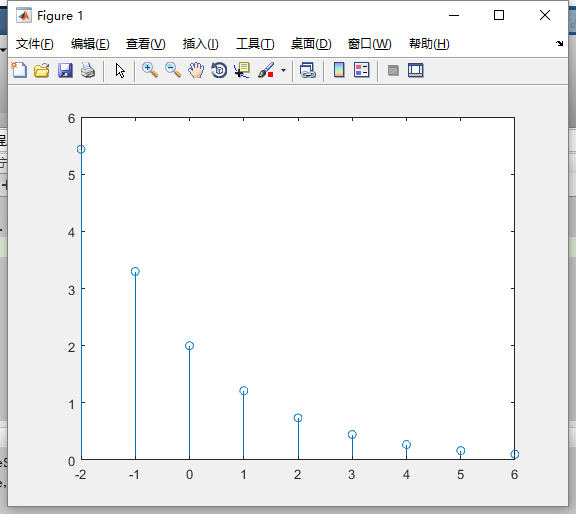
1)表示:x[n],图示为顶部带圈的竖线。
2)数字信号可用脉冲信号和阶跃信号表示
3)数字频率与模拟频率的转换:
在数字信号处理的学习中,很多刚入门朋友常常为模拟频率、数字频率及其相互之间的关系所迷惑,甚至是一些已经对数字信号处理有所了解的朋友也为这个问题所困惑。
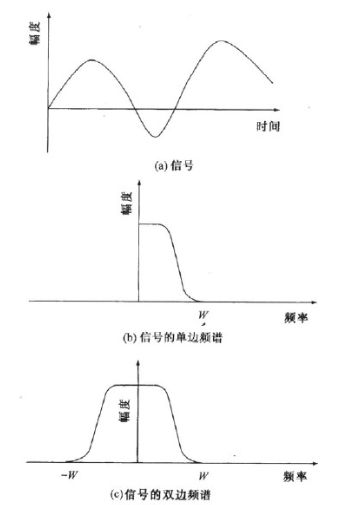
我们通常所说的频率,在没有特别指明的情况下,指的是模拟频率,其单位为赫兹(Hz),或者为1/秒(1/s),数学符号用f来表示。这是因为现实世界中的信号大多为模拟信号,频率是其重要的物理特性。以赫兹表示的模拟频率表示的是每秒时间内信号变化的周期数。如果用单位圆表示的话,如图1所示,旋转一圈表示信号变化一个周期,则模拟频率则指的是每秒时间内信号旋转的圈数。
模拟频率中还有一个概念是模拟角频率,数学符号常用Ω来表示,其单位为弧度/秒(rad/s)。从单位圆的角度看,模拟频率是每秒时间内信号旋转的圈数,每一圈的角度变化数为2pi。很显然,旋转f圈对应着2pi*f的弧度。即:
Ω=2pi*f(rad/s) (1)
数字信号大多是从模拟信号采样而得,采样频率通常用fs表示。数字频率更准确的叫法应该是归一化数字角频率,其单位为弧度(rad),数学符号常用ω表示。即:
ω=2pi*f/fs(rad) (2)
其物理意义是相邻两个采样点之间所变化的弧度数,如图1所示。
有了公式(1)和(2),我们就可以在模拟频率与数字频率之间随意切换。假定有一个正弦信号x[n],其频率f=100Hz,幅度为A,初始相位为0,则这个信号用公式可以表示为:
x(t) =A*sin(2*pi*100*t)
用采样频率fs=500Hz对其进行采样,得到的数字信号x[n]为:
x[n] =A*sin(2*pi*100*n/fs)= A*sin(0.4*pi*n)
很明显,这个数字信号的频率为0.4pi。
由上述讨论可知,对应两个数字频率完全相同的信号,其模拟频率未必相同,因为这里还要考虑采样频率。这种归一化为处理带来了方便,带也给理解带来了困惑。在数字信号中,虽然经常不显式地出现采样频率,但它却是架起模拟信号与数字信号的桥梁,对信号处理的过程有举足轻重的影响。
---------------------
作者:deepdsp
来源:CSDN
原文:https://blog.csdn.net/deepdsp/article/details/7272186
MATLAB应用:
t = 0:1/100:0.05;%时间刻度:最小时间:采样间隔:最大时间值 y = sin(2*t)-1;%笼络线函数 stem(t,y)%绘制离散数据序列
n = -2:6;%给定离散点范围 y = 2*exp(-0.5*n);%给定离散值函数 stem(n,y) %绘制离散数据序列
(3)数字信号处理:将信号输入计算机内进行分析处理。
(4)带限信号:信号有可确定的最大频率
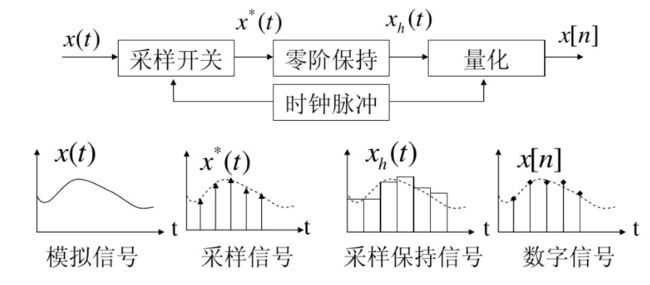
2.数字信号处理系统
(1)信号获取方式
自然界模拟信号通过各种传感器,将模拟量转化为模拟电信号,如声音信号可以由麦克风捕获,并转化为电信号;图像信号可由照相机捕获并转化为电信号。
MATLAB采集信号
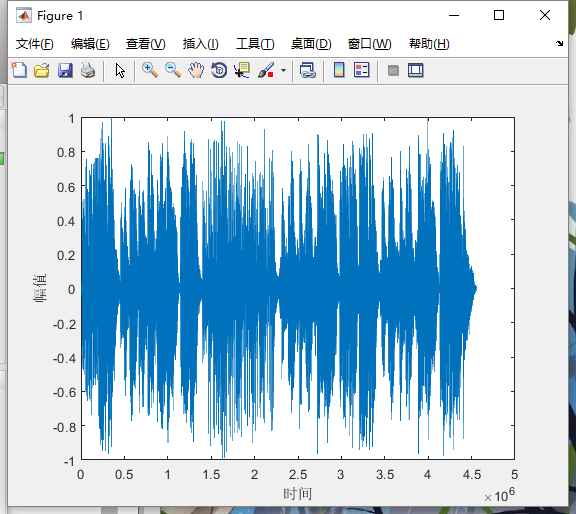
%============= % 首先用windows"开始->"程序"->"附件"-> % "娱乐"->"录音机"录入自己的语音,存成xx.wma文件; ============ [x,Fs]=audioread('D: test.wma'); %写出文件路径 y=x(:,1); %采集单声道? sound(y,Fs);%播放声音 figure; plot(y); xlabel('时间');ylabel('幅值'); %画时域图
程序说明:
[x,fs]=audioread(‘D:test.wma');%把语音信号进行加载,放入MATLAB仿真软件平台中,采样值放在向量x中,fs表示采样频率(Hz)。
y=x(:,1);%对双声道信号取单声道
(2)抗混叠滤波器
许多信号不是带限信号,如果最大频率未知,则不可能避免混叠。为解决这个问题,采样前先将信号通过模拟低通滤波器进行低通滤波,使信号成为带限信号,可以用足够高的采样频率来避免混叠。
作用:从要被采样的信号中消除了所有超过奈奎斯特频率的信号分量,以确保奈奎斯特采样将足以完整地记录信号。同时消除了所有超过奈奎斯特频率的噪声,防止高频噪声对有用信号的干扰。
(3)模数转换
a.采样(横坐标离散化)
采样时刻通常处在固定的间隔点上,这个间隔称为采样周期;
每一个点采样结束后要进行保持,直到下一个采样点,这个过程称为采样保持;
采样频率要大于采样信号最高频率的两倍(不能等于)——混叠现象;
采样需要占用有限的时间,称为采样器的采样时间;若不计采样时间则图如下,若计入采样时间则采样保持。信号先短暂跟随被采样的模拟信号,然后达到水平保持状态。
采样分为过采样和欠采样,欠采样会导致高于采样频率一般的频率将折返还原成低频信号。
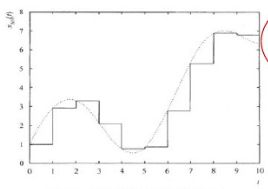
实际采样过程如下图
b.量化(纵坐标离散化):
量化步长:
量化误差:量化值-实际值
量化器的动态范围:
量化方案:从模拟范围的最小值开始,将量化电平分配给第一个半间隔而不是第一个整间隔,则量化误差要小一半,且为量化步长的一半。
信噪比判断信号与噪声的区分的难易程度。信噪比越大,信号越强。
当最大可容许量化误差电平确定后,可以计算量化比特数:
c.模数转换的数字信号特点
所允许的数字信号的取值个数是由计算机所用比特数限定的
数字信号仅在采样时刻有效,在采样点之间没有定义。
(4)数模转换
a.转化模拟电平
b.平滑零阶保持信号
(5)抗镜像滤波器
当由采样值恢复原信号时,重叠的问题就很重要。它可以通过低通滤波器解决,低频可以通过,而高频分量被衰减。该滤波器可以从频域里的所有镜像中选出与原频谱相符的频谱。
作用:在滤除不必要的高频信号的同时,也滤除了带外噪声。