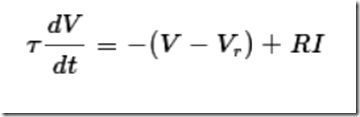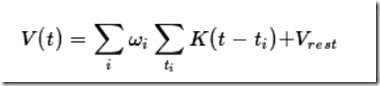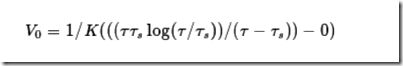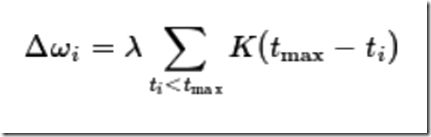接下来一段时间开启脉冲神经网络模型的探索之旅。脉冲神经网络有更强的生物学基础，尽可能地模拟生物神经元之间的连接和通信方式。其潜在能力较强，值得踏进一步探索。
构建脉冲神经网络模型，至少需要考虑三点：
1. 外界刺激编码
2. 构建神经元模型
3. 制定学习规则
外界刺激的编码方式主要有Rate Coding和Temporal Coding等，这里不在细述。而Hodgkin和Huxley两位研究员早在1952年就提出了第一个神经元模型：HH[1]。随后陆续有各种神经元模型被提出，其中具有代表性的为Izhikevich模型[2]和LIF(Leaky-Integrate-and-Fire)模型[3]。
以LIF神经元模型为例，其数学表达形式如下：
其中，
为膜时间常数， 为膜电阻， 为膜电导，
为膜电位，
为复位电位，
为注入电流。当膜电位超过一个固定的阈值时，神经元发放一个脉冲，并很快地降至复位电位并维持一小段时间，然后接受前段突触的输入脉冲重新升高膜电位。各种神经元模型均类似于此过程。
学习规则又分为无监督和有监督，其中无监督学习方法以STDP（Spike-Timing-Dependent Plasticity）[4,5]为代表，而有监督学习包括Tempotron[6]，ReSuMe（Remote Supervised Method）[7]和SpikeProp[8]等。
以Tempotron为例，阈值下的后突触膜电位(PSPs, Postsynaptic Potentials)为所有输入脉冲的加权和：
其中，
表示第
个输入神经元的脉冲发放时刻（注：输入神经元在一个时间窗口内可能发放多个脉冲，也可能没有脉冲发放）。
-
为输入神经元的第 个发放脉冲对后突触膜电位的贡献，具体为：
其中， 和
为时间常数。为使得- 的幅值为1，先设定
，然后求导得到最大膜电位时间代入
-
，求其倒数得到归一化因子
为：
绘制
随时间变化的曲线如下：
有监督学习的重点是如何更新突触连接权重
，获得期望输出脉冲。而Tempotron算法的核心如下：
以二分类问题为例，如上更新规则为：首先分别求取类别1和类别2的最大膜电位时刻 。假定样本为类别1时，输出神经元发放脉冲，而当样本为类别2时输出神经元不发放脉冲。那么只需要判断最大膜电位 与阈值电位
的关系即可进行权重更新：
（1）如当样本的真实类别为类别1，输入脉冲神经网络之后，输出神经元在当前窗口时间范围内的最大膜电位大于阈值电位，则发放一个脉冲且无需更新突触连接权重。而当最大膜电位小于阈值电位时，需要根据如上公式更新连接权重，且
以增强贡献比较大的连接权重。
（2）反之，如当样本的真实类别为类别2，输入脉冲神经网络之后，输出神经元在当前窗口时间范围内的最大膜电位小于阈值电位，则不发放脉冲且无需更新突触连接权重。而当最大膜电位大于阈值电位时，需要根据如上公式更新连接权重，且
以削弱贡献比较大的连接权重。
Github上有两个基于Python的Tempotron实现代码
其中一个为Ajay Karpur提供的：https://github.com/ajaykarpur/tempotron-classifier，利用Tempotron进行MNIST分类，但是该代码的Tempotron部分没有写完整，存在比较大的问题，不建议参考。
另外一个代码是由目前在荷兰阿姆斯特丹大学，逻辑、语言和计算研究所的美女博士Dieuwke Hupkes提供，代码写的非常优雅：https://github.com/dieuwkehupkes/Tempotron，细节解释的也很清楚。
利用Tempotron学习规则进行简单的二分类训练，通过下图可以看到输出膜电位的变化。其中，raw为训练前的膜电位曲线，trained为训练后的膜电位曲线。可见，训练后的Positive类别仍然发放脉冲，而训练后的Negative类别样本被抑制发放脉冲。
该学习算法较为简单，其目前的主要缺点均为输出单个脉冲所致，如：
（1）无法直接做为下一层神经元的输入，因而不易扩展为深层脉冲神经网络；
（2）输出的单个脉冲不便于做序列预测。
因而，考虑学习一下其他的有监督学习算法，如ReSuMe[7]和SpikeProp[8]等。
[1] Hodgkin A L, Huxley A F. A quantitative description of membrane current and its application to conduction and excitation in nerve[J]. The Journal of physiology, 1952, 117(4): 500.
[2] Izhikevich E M. Simple model of spiking neurons[J]. IEEE Transactions on neural networks, 2003, 14(6): 1569-1572.
[3] Gerstner W, Kistler W M. Spiking neuron models: Single neurons, populations, plasticity[M]. Cambridge university press, 2002.
[4]. Markram H, Lübke J, Frotscher M, et al. Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs[J]. Science, 1997, 275(5297): 213-215.
[5]. Bi G, Poo M. Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type[J]. Journal of neuroscience, 1998, 18(24): 10464-10472.
[6]. Gütig R, Sompolinsky H. The tempotron: a neuron that learns spike timing–based decisions[J]. Nature neuroscience, 2006, 9(3): 420-428.
[7]. Ponulak F. ReSuMe-new supervised learning method for Spiking Neural Networks[J]. Institute of Control and Information Engineering, Poznan University of Technology.(Available online at: http://d1. cie. put. poznan. pl/~ fp/research. html), 2005.
[8]. Bohte S M, Kok J N, La Poutre H. Error-backpropagation in temporally encoded networks of spiking neurons[J]. Neurocomputing, 2002, 48(1): 17-37.
转自：http://jacoxu.com/tempotron/