python数据分析实战之AQI分析
文章目录
- 1、数据分析的基本流程
- 2、明确需求和目的
- 2.1 需求和目的
- 3、数据收集
- 4、数据预处理
- 4.1 数据整合
- 4.1.1 加载相关库和数据集
- 4.1.2 数据总体概览
- 4.2 数据清洗
- 4.2.1 缺失值的处理
- 4.2.2 异常值的处理
- 4.2.3 重复值的处理
- 5、数据分析
- 5.1 描述性统计分析
- (1)哪些城市的空气质量较好/较差?
- (2)对城市的空气质量按照等级划分,每个等级城市数量分布情况如何?
- (3)空气质量在地理位置分布上,是否具有一定的规律性?
- 5.2 推断统计分析
- (1)临海城市的空气质量是否有别于内陆城市?
- (2)全国城市空气质量普遍处于何种水平?
- 5.3 相关系数分析
- (1)空气质量主要受哪些因素影响?
- 6、编写报告
1、数据分析的基本流程
- 明确需求和目的
- 数据收集(内部数据、购买数据、爬取数据、调查问卷、其它收集)
- 数据预处理(数据整合、数据清洗、数据转换等)
- 数据分析(描述分析、推断分析、数据建模、数据可视化等)
- 编写报告
2、明确需求和目的
- AQI:空气质量指数,用来衡量空气清洁或污染的程度,值越小,表示空气质量越好。
2.1 需求和目的
运用数据分析的相关技术,对全国城市空气质量进行研究和分析,解决以下问题:
- 哪些城市的空气质量较好/较差?(描述性统计分析)
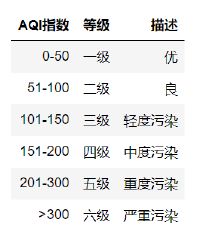
- 对城市的空气质量按照如下等级划分,每个等级城市数量分布情况如何?(描述性统计分析)
- 空气质量在地理位置分布上,是否具有一定的规律性?(描述性统计分析)
- 临海城市的空气质量是否有别于内陆城市?(推断统计分析)
- 全国城市空气质量普遍处于何种水平?(推断统计分析)
- 空气质量主要受哪些因素影响?(相关系数分析)
3、数据收集
4、数据预处理
4.1 数据整合
4.1.1 加载相关库和数据集
- 使用的库主要有:pandas、numpy、matplotlib、seaborn
- 使用的数据集:2015年空气质量指数(AQI)数据集
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
sns.set(style="darkgrid")
plt.rcParams["font.family"] = "SimHei" # 设置可以显示中文字体
plt.rcParams["axes.unicode_minus"] = False
warnings.filterwarnings("ignore") # 忽略警告信息
data = pd.read_csv("AQI_data.csv")
4.1.2 数据总体概览
print(data.info()) # 展示data的概览信息
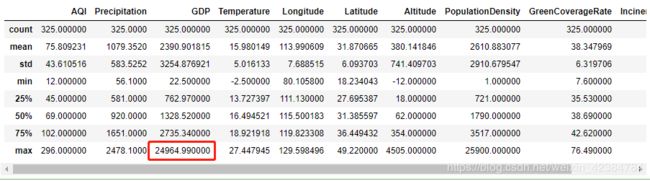
print(data.describe()) # 展示data 数值类型字段的统计信息
print(data.sample(5)) # 随机抽样10条数据
4.2 数据清洗
4.2.1 缺失值的处理
查看缺失值:
- data.info()
- data.isnull()
data.isnull().sum(axis=0) # 查看缺失值
-----------------------------------------
City 0
AQI 0
Precipitation 4
GDP 0
Temperature 0
Longitude 0
Latitude 0
Altitude 0
PopulationDensity 0
Coastal 0
GreenCoverageRate 0
Incineration(10,000ton) 0
dtype: int64
缺失值处理方式:
- 删除缺失值(仅仅适合缺失数量较少的情况)
- 填充缺失值(数值变量使用均值或中位数进行填充,类别变量使用众数填充或单独作为一个类别)
- 缺失值小于20%,直接填充。
- 缺失值在20%-80%之间,填充变量后,同时增加一列,标记该列是否缺失,参与后续建模。
- 缺失值大于80%,不使用原始列,而是增加一列,标记该列是否缺失,参与后续建模。
从上面可以看出,"Precipitation"存在4个缺失值,数量较少,可以直接使用中位数进行填充:
data.fillna({"Precipitation": data["Precipitation"].median()}, inplace=True)
data.isnull().sum(axis=0) # 再次查看缺失值,验证效果,此时已没有缺失值
4.2.2 异常值的处理
查看异常值:
- data.describe(),仅能作为一种简单的方式。
- 3 δ 方式:根据正态分布的特性,可以将3 δ之外的数据,视为异常值。
- 箱线图:箱线图是一种常见的异常检测方式。
- 相关异常检测算法
data.describe()
通过describe()方法可以看出GDP存在异常值,用3 δ 方式进一步查看:
mean, std = data["GDP"].mean(), data["GDP"].std()
min_, max_ = mean - 3 * std, mean + 3 * std
data["GDP"][(data["GDP"] < min_) | (data["GDP"] > max_)]
-------------------------------------
16 22968.60
63 18100.41
202 24964.99
207 17502.99
215 14504.07
230 16538.19
256 17900.00
314 15719.72
Name: GDP, dtype: float64
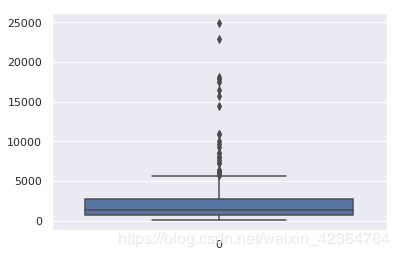
还可以通过箱线图进行查看:
sns.boxplot(data=data["GDP"])
异常值处理方式:
- 删除异常值
- 视为缺失值处理
- 对数转换:如果数据中存在较大的异常值,通过取对数来进行转换,可以得到一定的缓解。(适合右偏分布,不适合左偏分布)
- 使用临界值进行填充:对异常值进行“截断”处理,使用临界值替换异常值。
- 使用分箱法离散化处理:如果特征对目标值的影响不是线性增加的,可以使用分箱方式对特征进行离散化处理。
对于GDP来说,因为存在较大的异常值,所以可以使用对数转换进行处理:
fig, ax = plt.subplots(1, 2)
fig.set_size_inches(15, 5)
sns.distplot(data["GDP"], ax=ax[0]) # 原始数据
data["GDP"] = np.log(data["GDP"]) # 使用对数转换
sns.distplot(data["GDP"], ax=ax[1]) # 转换之后的数据

从上面可以看出,取对数之后,图像右偏分布情况得到一定程度的缓解。
4.2.3 重复值的处理
查看重复值:
- data.duplicated()
print(data.duplicated().sum()) # 查看重复值的数量
data[data.duplicated(keep=False)] # 查看哪些记录出现了重复值
重复值的处理:
- 重复值对于数据分析通常没有作用,直接删除即可。
data.drop_duplicates(inplace=True)
data.duplicated().sum() # 再次查看重复值的数量,验证删除效果
5、数据分析
5.1 描述性统计分析
(1)哪些城市的空气质量较好/较差?
city = data[["City", "AQI"]].sort_values("AQI") # 按照AQI进行排序
print(city.iloc[:5]) # 空气质量最好的5个城市
print(city.iloc[-5:]) # 空气质量最差的5个城市
(2)对城市的空气质量按照等级划分,每个等级城市数量分布情况如何?
# 编写函数,将AQI转换为对应的等级。
def value_to_level(AQI):
if AQI >= 0 and AQI <= 50:
return "一级"
elif AQI >= 51 and AQI <= 100:
return "二级"
elif AQI >= 101 and AQI <= 150:
return "三级"
elif AQI >= 151 and AQI <= 200:
return "四级"
elif AQI >= 201 and AQI <= 300:
return "五级"
else:
return "六级"
level = data["AQI"].apply(value_to_level) # 按照等级对城市进行划分
print(level.value_counts()) # 统计每个等级的数量分布
(3)空气质量在地理位置分布上,是否具有一定的规律性?
sns.scatterplot(x="Longitude", y="Latitude", hue="AQI", palette=plt.cm.RdYlGn_r, data=data) # 画出空气质量分布的散点图
从上图可以看出,从大致的地里位置分布上看,西部城市好于东部城市,南部城市好于北部城市。
5.2 推断统计分析
(1)临海城市的空气质量是否有别于内陆城市?
print(data["Coastal"].value_counts()) # 查看临海城市和内陆城市的数量分布
print(data.groupby("Coastal")["AQI"].mean()) # 分组统计AQI的均值
----------------------
Coastal
否 79.644898
是 64.062500
虽然从均值上看,临海城市的AQI更低,但还不能够说明临海城市空气一定比内陆城市好,还需要进行差异检验。
- 进行两样本t检验,来查看临海城市和内陆城市的均值差异是否显著。
from scipy import stats
coastal = data[data["Coastal"] == "是"]["AQI"]
inland = data[data["Coastal"] == "否"]["AQI"]
# 进行方差齐性检验。为后续的两样本t检验服务。
stats.levene(coastal, inland)
----------------
LeveneResult(statistic=0.03818483157315866, pvalue=0.8451953286335765)
# 进行两样本t检验。注意,两样本的方差相同与不相同,取得的结果是不同的。
r = stats.ttest_ind(coastal, inland, equal_var=True)
print(r)
p = stats.t.sf(r.statistic, df=len(coastal)+len(inland)-2)
print("P-Value值:",p)
----------------------
Ttest_indResult(statistic=-2.804017387113549, pvalue=0.005352397281668703)
P-Value值: 0.9973238013591657
从以上结果来看,P值为0.997,那么我们可以认为临海城市的空气质量确实要好于内陆城市。
(2)全国城市空气质量普遍处于何种水平?
mean = data["AQI"].mean()
std = data["AQI"].std()
# 求出空气质量指数 95%的置信区间
stats.t.interval(0.95, df=len(data) - 1, loc=mean, scale=std / np.sqrt(len(data)))
求出95%的置信区间,我们可以认为全国城市空气质量普遍处于该区间范围内。
5.3 相关系数分析
- 协方差:体现两个变量之间的分散性以及两个变量变化步调是否一致。
- 相关系数:体现两个连续变量之间的相关性,最为常用的是皮尔逊相关系数。
两个变量的相关系数,定义为:

相关系数的取值范围为[-1,1],我们可以根据相关系数的取值来衡量两个变量的相关性(负数表示负相关,步调相反):
- 0.8-1.0:极强相关
- 0.6-0.8:强相关
- 0.4-0.6:中等强度相关
- 0.2-0.4:弱相关
- 0.0-0.2:极弱相关或无相关
(1)空气质量主要受哪些因素影响?
x = data["AQI"]
y = data["Precipitation"]
a = (x - x.mean()) * (y - y.mean()) # 公式计算AQI与Precipitation的协方差。
cov = np.sum(a) / (len(a) - 1)
print("协方差:", cov)
corr = cov / np.sqrt(x.var() * y.var()) # 公式计算AQI与Precipitation的相关系数。
print("相关系数:", corr)
print("协方差:", x.cov(y)) # 内置方法计算协方差
print("相关系数:", x.corr(y)) # 内置方法计算相关系数
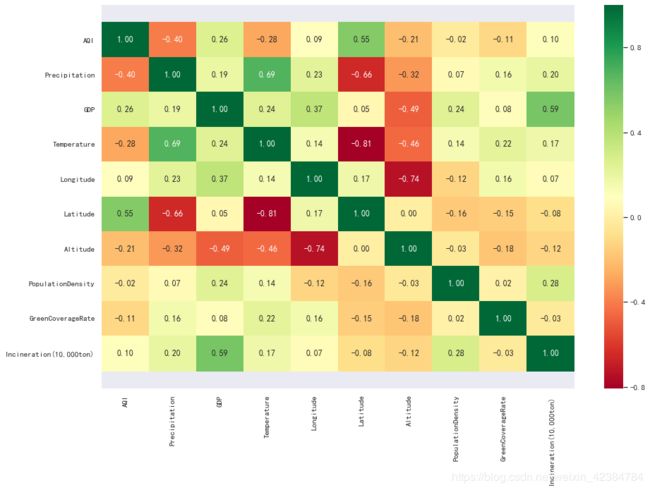
data.corr() # 内置方法计算所有特征之间的相关系数
plt.figure(figsize=(15, 10))
ax = sns.heatmap(data.corr(), cmap=plt.cm.RdYlGn, annot=True, fmt=".2f")
a, b = ax.get_ylim()
ax.set_ylim(a + 0.5, b - 0.5)
从以上结果可以看出:空气质量指数主要受降雨量(相关系数-0.40)和纬度(相关系数0.55)的影响。
6、编写报告
- 根据前面的分析,对结果进行汇总,得到分析报告。