【文献阅读及pytorch实践】Non-local Neural Networks

原文链接：http://arxiv.org/pdf/1711.07971v3
国内镜像：http://xxx.itp.ac.cn/pdf/1711.07971v3

---

卷积操作和递归操作都是构建块，一次处理一个局部邻居，在此文中，作者将非局部操作作为捕获远程依赖项的构建块的一个通用族来表示。受传统算法非局部均值启发，非局部操作用所有位置特征的加权来作为一个位置的响应。

我们从图像数据来解释，获得比较大的感受野是通过不断堆叠卷积，因为卷积是一个邻域操作，所以只能通过不断地重复传播需要远程依赖的信号。这样就有一些局限：
1.计算效率低
2.由于网络很深，优化困难
3.当需要在比较远位置之间来回传递消息时，这是局部操作是困难的

为了解决这个问题，并且受到了传统非局部均值滤波的启发，作者使用非局部均值操作。先来说主要贡献：

1.与递归操作和卷积操作的渐进行为不同，非局部操作通过计算任意两个位置之间的交互直接捕获远程依赖，而不管它们的位置距离

2.实验表明，非局部操作是有效的，即使只有几层，也能达到最佳效果

3.非局部操作保持了可变的输入大小，并且可以轻松地与其他操作相结合（比如卷积）

---

1.非局部均值滤波

非局部均值（non-local means）是经典滤波算法，通过计算图像中所有像素的加权平均值实现过滤。下面是非局部均值的计算公式：

x是当前要计算的点，y是与相关的点，w(x,y)是x,y之间的相似度，会被当作权重，v(y)是对y的变换。
具体计算过程如下：

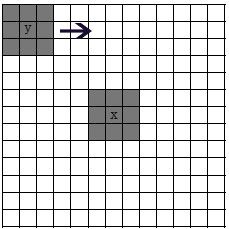
最大的框是搜索框I，也就是在计算x的时候，考虑相似像素的范围。图中3 * 3的小黑框是依赖邻域。
如果我们认为小邻域内所有点的重要性是一样的，那么计算x块和y块之间的欧式距离d为：

block(x)和block(y)就是两个矩阵，除以block_size也很好理解，归一化。
w(x,y)的计算公式如下：

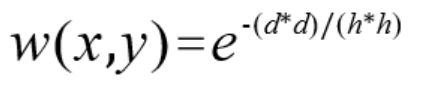
其中，h为衰减因子。h越小，则加权点对当前点的影响越小，一般边缘保持得好但是噪声会严重，反之则边缘保持差图像更加光滑。
算完权值后，就可以把搜索框内所有y的变换与加权值相乘再相加，即为算出的当前点的值：

计算欧式距离时，有时会考虑周围点对中心点的影响，会利用核函数对欧式距离加权，即加权因子重写为：

这里提供一个非均值kernel的算法：

对于图中3 * 3的邻域，算出的k为：

将其归一化，每个点结果为：

2.非局部操作

受到non-local means的启发，提出了关于non-local操作的通用表示，公式如下所示：

其中，i是要被计算的位置（可以是空间位置、时间位置、时空位置），j是要被用作加权的位置，x是输入，y是输出，f可以看作相似度，g是一个一元变化，C用作归一化。
上式中的j，对计算机视觉来说，是feature map中所有的位置。

非局部操作与全连接的区别如下：
1.在non-local操作的公式中，响应值是通过计算不同区域之间的关系得到的，而在全连接层中，是通过赋给每个神经元一个学到的权重。换而言之，在全连接层中，Xi和Xj的关系不能通过一个函数f得到
2.non-local公式支持可变大小的输入，并在输出中保持相应的大小；在全连接层中，要求固定大小的输入和输出，并且由于被拉伸成一列，丢失了原有的位置信息
3.在与CNN结合位置来看，non-local操作非常灵活，可以添加到深度神经网络中的前半部分，而全连接层通常被用在最后，这既是一个不同，也给了我们一个启发：能够构建一个更丰富的层次结构，将非局部信息和局部信息结合起来

为简单起见，我们只考虑线性嵌入形式的g: g(Xj) = WgXj，其中Wg是要学习的权值矩阵。
对于f函数，有如下几种实例化方法：

① Gaussian

函数的功能主要是相似度计算，一个通常的想法是利用点积衡量相似度（dot-product similarity），为什么点积可以衡量相似度呢，这可以通过余弦相似度公式简化而来，余弦相似度计算下式所示：

如果我们只用点积，相当于减少了计算量和计算复杂度，而且还能达到类似的效果。
那么，f函数可以用高斯函数表示如下：

那么此时归一化因子C(x)可以设置为：

② Embedded Gaussian

基于高斯函数的一个简单扩展，是计算嵌入空间中的相似度，即：

其中，θ和φ是两个嵌入，embedding会构建一个映射，将一个空间里的实体抛射到一个线性向量空间里去，这样一来可以在向量空间里计算度量它们的距离，即：

相应的，归一化因子C(x)可以表示为：

我们再来看看self-attention的公式：

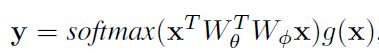
Embedded Gaussian操作与self-attention很类似，实际上，self-attention是其一个特例。

③ Dot Product

通过点乘进行相似度计算：

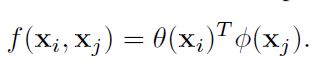
此时的归一化因子C(x)可以设置为N（所有位置数）。

dot product与embedded gaussian最主要的区别是softmax的使用，softmax起着激活的作用

④ Concatenation

其中，[·, ·] 表示维度拼接操作，Wf实现从向量到标量的转化。

3.非局部模块

非局部模块定义为：

其中，yi是非局部操作计算得出的，“+Xi”可以看作残差连接。之所以要用残差，是因为这种结构能够在不破坏原始网络结构的基础上，很方便的将non-local block嵌入模型中去。
所以最后构建的非局部模块如下所示：

上图的f函数可以替换为任何一个可计算相似度的函数。

4.实验结果及结论

1.可视化

non-local网络可以学习发现有意义的关系线索，不管空间还是时间。

2.实例化

不同的计算相似度的方法表现得很相似，没有很大的差异。实验表明，该模块的注意(softmax)行为并不是改善我们应用的关键;相反，更可能的情况是，非局部行为很重要，而且它对实例化不敏感。

3.在哪个阶段加入非局部块？

一个非局部块对res2、res3或res4的改进是相似的，而对res5的改进稍微小一些。一种可能的解释是res5的空间尺寸较小(7*7)，无法提供精确的空间信息。

4.加更多的非局部块

更多的非局部块通常会带来更好的结果。信息可以在时空中遥远的位置之间来回传递，这很难通过局部模型实现。
加了非局部块后，更小的深度（更少的参数）有更好的结果。
将非局部块换为残差块，结果没有变好，说明非局部块对结果的提升不仅仅是增加了深度。

5.回报高

我们看到一个单独的非局部块改进了所有的R50/101和X152基线，包括检测和分割的所有指标。这一比较表明，尽管增加了深度/容量，但现有模型并没有充分捕获非局部依赖关系。
此外，上述收益是在一个非常小的成本。单个非局部块仅向基线模型添加<5%的计算；尝试使用更多的非局部块到主干，但发现回报递减。

pytorch代码

github：https://github.com/WangChenxu21/self-attention
参数的初始化是个讲究，目前听到的说法是最好将残差块的最后一个的参数设为0，这样就最起码是恒等映射，便于优化。

import torch
import torch.nn as nn
import torch.nn.functional as F


__all__ = ['Gaussian', 'EmbeddedGaussian', 'DotProduct', 'Concatenation']


class Gaussian(nn.Module):
    def __init__(self, in_channels, inter_channels=None, sub_sample=True, bn_layer=True):
        super(Gaussian, self).__init__()

        self.in_channels = in_channels
        self.inter_channels = inter_channels
        self.sub_sample = sub_sample

        if self.inter_channels == None:
            self.inter_channels = in_channels // 2
            if self.inter_channels == 0:
                self.inter_channels = 1

        if bn_layer:
            self.W = nn.Sequential(
                nn.Conv2d(self.inter_channels, in_channels, 1),
                nn.BatchNorm2d(in_channels),
            )
            nn.init.constant_(self.W[1].weight, 0)
            nn.init.constant_(self.W[1].bias, 0)
        else:
            self.W = nn.Conv2d(self.inter_channels, in_channels, 1)
            nn.init.constant_(self.W.weight, 0)
            nn.init.constant_(self.W.bias, 0)

        self.g = nn.Conv2d(in_channels, self.inter_channels, 1)

        if sub_sample:
            self.g = nn.Sequential(self.g, nn.MaxPool2d(2, stride=2))
            self.phi = nn.MaxPool2d(2, stride=2)

    def forward(self, x):
        batch_size = x.size(0)

        g_x = self.g(x).reshape(batch_size, self.inter_channels, -1)
        g_x = g_x.permute(0, 2, 1)

        theta_x = x.reshape(batch_size, self.in_channels, -1)
        theta_x = theta_x.permute(0, 2, 1)

        if self.sub_sample:
            phi_x = self.phi(x).reshape(batch_size, self.in_channels, -1)
        else:
            phi_x = x.reshape(batch_size, self.in_channels, -1)

        f = torch.matmul(theta_x, phi_x)
        f_div_C = F.softmax(f, dim=-1)

        y = torch.matmul(f_div_C, g_x).permute(0, 2, 1)
        y = y.reshape(batch_size, self.inter_channels, *x.size()[2:])

        W_y = self.W(y)
        z = W_y + x

        return z


class EmbeddedGaussian(nn.Module):
    def __init__(self, in_channels, inter_channels=None, sub_sample=True, bn_layer=True):
        super(EmbeddedGaussian, self).__init__()

        self.inter_channels = inter_channels

        if self.inter_channels == None:
            self.inter_channels = in_channels // 2
            if self.inter_channels == 0:
                self.inter_channels = 1

        if bn_layer:
            self.W = nn.Sequential(
                nn.Conv2d(self.inter_channels, in_channels, 1),
                nn.BatchNorm2d(in_channels),
            )
            nn.init.constant_(self.W[1].weight, 0)
            nn.init.constant_(self.W[1].bias, 0)
        else:
            self.W = nn.Conv2d(self.inter_channels, in_channels, 1)
            nn.init.constant_(self.W.weight, 0)
            nn.init.constant_(self.W.bias, 0)

        self.g = nn.Conv2d(in_channels, self.inter_channels, 1)
        self.theta = nn.Conv2d(in_channels, self.inter_channels, 1)
        self.phi = nn.Conv2d(in_channels, self.inter_channels, 1)

        if sub_sample:
            self.g = nn.Sequential(self.g, nn.MaxPool2d(2, stride=2))
            self.phi = nn.Sequential(self.phi, nn.MaxPool2d(2, stride=2))

    def forward(self, x):
        batch_size = x.size(0)

        g_x = self.g(x).reshape(batch_size, self.inter_channels, -1)
        g_x = g_x.permute(0, 2, 1)

        theta_x = self.theta(x).reshape(batch_size, self.inter_channels, -1)
        theta_x = theta_x.permute(0, 2, 1)

        phi_x = self.phi(x).reshape(batch_size, self.inter_channels, -1)

        f = torch.matmul(theta_x, phi_x)
        f_div_C = F.softmax(f, dim=-1)

        y = torch.matmul(f_div_C, g_x).permute(0, 2, 1)
        y = y.reshape(batch_size, self.inter_channels, *x.size()[2:])

        W_y = self.W(y)
        z = W_y + x

        return z


class DotProduct(nn.Module):
    def __init__(self, in_channels, inter_channels=None, sub_sample=True, bn_layer=True):
        super(DotProduct, self).__init__()

        self.inter_channels = inter_channels

        if self.inter_channels == None:
            self.inter_channels = in_channels // 2
            if self.inter_channels == 0:
                self.inter_channels = 1

        if bn_layer:
            self.W = nn.Sequential(
                nn.Conv2d(self.inter_channels, in_channels, 1),
                nn.BatchNorm2d(in_channels),
            )
            nn.init.constant_(self.W[1].weight, 0)
            nn.init.constant_(self.W[1].bias, 0)
        else:
            self.W = nn.Conv2d(self.inter_channels, in_channels, 1)
            nn.init.constant_(self.W.weight, 0)
            nn.init.constant_(self.W.bias, 0)

        self.g = nn.Conv2d(in_channels, self.inter_channels, 1)
        self.theta = nn.Conv2d(in_channels, self.inter_channels, 1)
        self.phi = nn.Conv2d(in_channels, self.inter_channels, 1)

        if bn_layer:
            self.g = nn.Sequential(self.g, nn.MaxPool2d(2, stride=2))
            self.phi = nn.Sequential(self.phi, nn.MaxPool2d(2, stride=2))

    def forward(self, x):
        batch_size = x.size(0)

        g_x = self.g(x).reshape(batch_size, self.inter_channels, -1)
        g_x = g_x.permute(0, 2, 1)

        theta_x = self.theta(x).reshape(batch_size, self.inter_channels, -1)
        theta_x = theta_x.permute(0, 2, 1)

        phi_x = self.phi(x).reshape(batch_size, self.inter_channels, -1)

        f = torch.matmul(theta_x, phi_x)
        f_div_C = f / f.size(-1)

        y = torch.matmul(f_div_C, g_x).permute(0, 2, 1)
        y = y.reshape(batch_size, self.inter_channels, *x.size()[2:])

        W_y = self.W(y)
        z = W_y + x

        return z


class Concatenation(nn.Module):
    def __init__(self, in_channels, inter_channels=None, sub_sample=True, bn_layer=True):
        super(Concatenation, self).__init__()

        self.inter_channels = inter_channels

        if self.inter_channels == None:
            self.inter_channels = in_channels // 2
            if self.inter_channels == 0:
                self.inter_channels = 1

        if bn_layer:
            self.W = nn.Sequential(
                nn.Conv2d(self.inter_channels, in_channels, 1),
                nn.BatchNorm2d(in_channels),
            )
            nn.init.constant_(self.W[1].weight, 0)
            nn.init.constant_(self.W[1].bias, 0)
        else:
            self.W = nn.Conv2d(self.inter_channels, in_channels, 1)
            nn.init.constant_(self.W.weight, 0)
            nn.init.constant_(self.W.bias, 0)

        self.g = nn.Conv2d(in_channels, self.inter_channels, 1)
        self.theta = nn.Conv2d(in_channels, self.inter_channels, 1)
        self.phi = nn.Conv2d(in_channels, self.inter_channels, 1)

        if sub_sample:
            self.g = nn.Sequential(self.g, nn.MaxPool2d(2, stride=2))
            self.phi = nn.Sequential(self.phi, nn.MaxPool2d(2, stride=2))

        self.concat_project = nn.Sequential(
            nn.Conv2d(self.inter_channels * 2, 1, 1, bias=False),
            nn.ReLU(),
        )

    def forward(self, x):
        batch_size = x.size(0)

        g_x = self.g(x).reshape(batch_size, self.inter_channels, -1)
        g_x = g_x.permute(0, 2, 1)

        theta_x = self.theta(x).reshape(batch_size, self.inter_channels, -1, 1)
        phi_x = self.phi(x).reshape(batch_size, self.inter_channels, 1, -1)
        theta_num = theta_x.size(2)
        phi_num = phi_x.size(3)
        theta_x = theta_x.repeat(1, 1, 1, phi_num)
        phi_x = phi_x.repeat(1, 1, theta_num, 1)

        f_concat = torch.cat([theta_x, phi_x], dim=1)
        f = self.concat_project(f_concat)
        f = f.reshape(batch_size, theta_num, phi_num)
        f_div_C = f / f.size(-1)

        y = torch.matmul(f_div_C, g_x).permute(0, 2, 1)
        y = y.reshape(batch_size, self.inter_channels, *x.size()[2:])

        W_y = self.W(y)
        z = W_y + x

        return z