SuperPCA:用于高光谱图像无监督特征提取的超像素PCA方法
SuperPCA: A Superpixelwise PCA Approach for Unsupervised Feature Extraction of Hyperspectral Imagery
作者 :Junjun Jiang, Jiayi Ma, Chen Chen, Zhongyuan Wang, Zhihua Cai, and Lizhe Wang
摘要
主成分分析(PCA)作为一种无监督降维方法,它在全局范围内提取最具代表性的波段,然而不同的同质区域对应于不同的物体,其光谱特征是多样的,这种对整体进行统一预测的方法显然是不合适的,因此本文提出了超像素PCA方法(SuperPCA)用于学习HSI的内在低维特征。
介绍
基于SuperPCA的HSI降维原理图如下图1所示。首先通过超像素分割将一个HSI分割成多个均匀区域,用矩阵表示,矩阵的列是像素的谱向量。然后将PCA应用于这些高维矩阵,得到降维矩阵。最后,我们将这些低维矩阵重新排列组合,形成降维的高光谱图像。

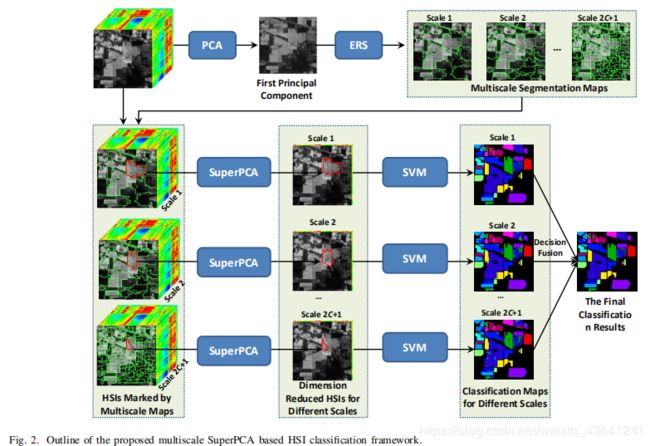
为了充分利用HSI立方体中包含的空间信息,文中进一步提出了一种基于多尺度分割的超pca模型,即MSuperPCA,它可以有效地集成多尺度空间信息,通过决策融合得到最优的分类结果。下图2为MSuperPCA的框架图。MSuperPCA的步骤大致可总结如下:
① 首先运用PCA得到图像的第一主成分
② 然后对第一主成分运用熵率超像素(ERS)进行超像素分割,通过设置不同的超像素数量即可得到多尺度超像素。
③ 然后,针对每个尺度,采用超pca得到降维后的图像
④ 运用基于支持向量机(SVM)分类器对不同尺度进行预测
⑤ 最后采用多数投票决策融合策略生成最终的分类结果
SuperPCA
全局PCA考虑整个数据空间,并寻找该空间的最佳转换向量,他可能会忽略同质区域的差异,如下图中的例子所示,假设数据空间由第1类(蓝色方块)和第2类(橙色方块)构成,这两类可能代表了图像中两个不同均匀区域的样本分布,图中可看出第1类和第2类的变换向量w1和w2是显著不同的,它们也不同于为整个数据空间生成的变换向量w。

鉴于上述问题,本文提出了一种基于PCA的分治策略来对每个均匀区域进行无监督特征提取。首先用PCA得到图像的第一主成分,然后使用ERS得到超像素分割。文章提出一种基于多尺度像素分割的策略增强了单尺度分割的性能,即设置不同的超像素数量( S c S_c Sc)分分割图像,得到多个不同尺度的分割图,具体地说,将图像的第一主成分 I f I_f If分割为 2 C + 1 2C+1 2C+1个尺度,第c个尺度的像素数量为:
S c = ( 2 ) c S f , c = 0 , ± 1 , ± 2 , ⋯ , ± C , S_c = (\sqrt{2})^{c}S_f, c = 0,\pm1,\pm2,\cdots,\pm C, Sc=(2)cSf,c=0,±1,±2,⋯,±C,(公式中 S f S_f Sf为根据经验设置的超像素基本数量)
对于分割后的多尺度图像,最后采取决策融合策略,即融合不同尺度中每个像素的类别标签,在此文中采用多数票决的决策融合策略,如下公式所示:
l = a r g m a x i ∈ { 1 , 2 , . . . , G } N ( i ) , N ( i ) = ∑ j = 1 2 C + 1 α j I ( l j = i ) , l = \underset{i\in\{1,2,...,G\}}{\mathrm{argmax}} N(i), N(i) = \sum_{j=1}^{2C+1} \alpha_jI(l_j = i), l=i∈{1,2,...,G}argmaxN(i),N(i)=∑j=12C+1αjI(lj=i),
这里 l l l是 G G G个可能类别中的一个类别, N ( i ) N(i) N(i)表示了类别 i i i被预测的次数, I I I是指示函数 α j \alpha_j αj表示第j个分类器的投票权重,我们使用等投票权所以 α j = 1 2 C + 1 ( j = 1 , 2 , . . . , 2 C + 1 ) \alpha_j=\frac{1}{2C+1}(j=1,2,...,2C+1) αj=2C+11(j=1,2,...,2C+1)。
实验分析
在对参数的实验中,文章主要测试了两个主要参数一是超像素的数量 S f S_f Sf,二是尺度的数量。
(1)对参数 S f S_f Sf的实验分析可得到两个结论,一是随着 S f S_f Sf的增多,准确率先上升后下降, S f S_f Sf太大太小都不好,主要是因为太大会导致区域过分割,不能充分利用同质区域的所有样本,太小则导致欠分割,样本会来自多种同质区域;二是通过设置一定数量的超像素总是比传统PCA的效果好,因为SuperPCA考虑了图像的空间均匀性。

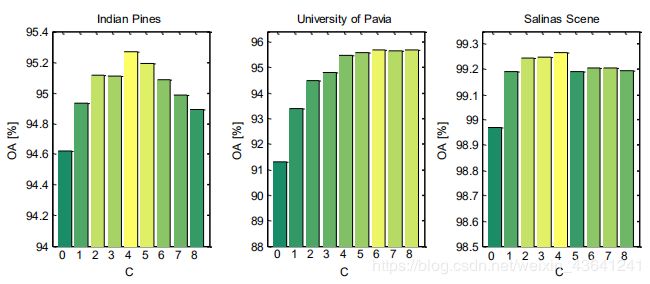
(2)对尺度数量的实验分析中,作者首先测试单一尺度的实验效果,将 c c c设置到-5到5,分别测试其不同尺度大小时的结果, c = 0 c=0 c=0表示用基本的超像素分割。从表中(Indian Pine数据集)可以看出,在基本的超像素数 S f S_f Sf下,它不能在每一个类中都取得最好的性能,当 c = − 4 c=-4 c=−4时,OA明显低于最佳效果(94.62%),然而,在这种情况下,第6类和第8类获得了最佳的分类精度。这些结果表明,基于单一尺度的超像素分割不能完全模拟图像的复杂性和多样性。因此,基于多尺度分割的决策融合是一种更可靠的选择。

接着文中便测试了融合多尺度分割的效果,通过融合基于多尺度分割的分类结果,可以得到比单尺度超主成分分析更好的分类结果,与此同时,观察到比其他两个HSI数据集规模都大的帕维亚大学的最优规模数量为6,可得到另一个现象:为了实现分类精度高,相对复杂的图像可能需要更大的规模数量利用空间信息。
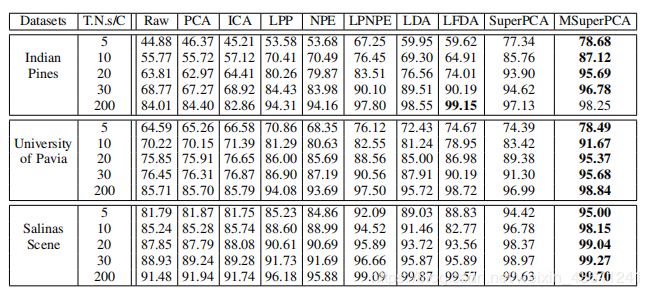
最后该方法在与其他方法的对比实验中可以看出在训练样本数量较少的情况下,该方法可以取得较好的效果。即使在训练样本较大时SuperPCA没有使用任何标签信息,结果仍然是非常有竞争力的。
结论
这篇文章提出了一种基于超pca的多尺度分割决策融合模型(MSuperPCA),通过将整个高光谱图像分割成多个不同均匀区域可以更方便的进行降维处理得到图像本质的低维特征空间,通过多尺度融合可以充分利用图像中包含的单尺度无法提取的空间信息。MSuperPCA算法在训练样本有限的情况下,具有明显的优势。另外,该方法继承了传统PCA的优点,在其他高光谱图像的预处理中使用它替换传统PCA方法可能会取得更好的效果。