计算机组成原理复习(三):2.运算方法和运算器(二)
2.运算方法和运算器(二)
前言
- “加减乘除”的本质都是“加法”
- “加法”的本质就是位运算(异或+与)
- 位运算的本质就是逻辑门电路
后面,我会用c语言只用位运算模拟一个加法,然后用这个加法实现“加减乘除”
定点加法、减法运算
定点加法
这个要讲的其实不多,直接看例子吧:
【例1】x = +1001,y = +0101,求x+y
解:[x]补 = 0 1001,[y]补 = 0 0101
0 1001
+ 0 0101
-----------
0 1110
∴x + y = +1110
【例2】x = +1011,y = -0101,求x+y
解:[x]补 = 0 1011,[y]补 = 1 1011
0 1011
+ 1 1011
-----------
[1]0 0110
∴x + y = +0110
讲讲注意点吧:
- 符号位也要参与运算
- 超出的进位要舍去
定点减法
还记得我说的那句话吗?减法的本质就是加法:[x-y] = [x] - [y] = [x] + [-y]
还是直接上例子吧:
【例1】x = -1110,y = +1101,求[x]补、[-x]补、[y]补、[-y]补
[x] = 1 0010
[-x] = 0 1110
[y] = 0 1101
[-y] = 1 0011
【例2】x = +1101,y = +0110,求x-y
解:[x]补 = 0 1101,[-y]补 = 1 1010
0 1101
+ 1 1010
-----------
[1]0 0111
∴x - y = +0111
溢出与检测
运算中,两个数相加,如果大于字长,直接溢出,那不是贼伤,比如:
0 1011
+ 0 1001
-----------
1 0100
==============
1 0011
+ 1 0101
-----------
0 1000
正数+正数=负数?此为正溢。
负数+负数=正数?此为负溢。
那咋办嘛?好办,引入双符号位法(也就是变形补码):
- 00:正数
- 01:正溢
- 10:负溢
- 11:负数
上例子:
【例1】x = +1100,y = +1000,求x+y
解:[x]补 = 00 1100,[y]补 = 00 1000
00 1100
+ 00 1000
------------
01 0100
∴x + y 正溢出啦
【例2】x = -1100,y = -1000,求x-y
解:[x]补 = 11 0100,[y]补 = 11 1000
11 0100
+ 11 1000
------------
10 1100
∴x + y 负溢出啦
规律其实很简单,两个符号为相同就没毛病,不相同就出问题
诶,要是我不想双符号位,我就只想用单符号可以吗?当然可以!
来,再看一遍这个例子:
0 1011
+ 0 1001
-----------
1 0100
==============
1 0011
+ 1 0101
-----------
0 1000
-
正溢出:最高有效位有进位,符号位无进位
-
负溢出:最高有效位无进位,符号位有进位
牛逼吧?
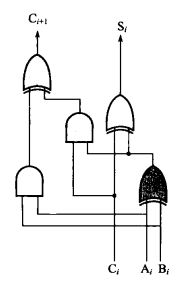
最基本的二进制加/减法器
我们硬核点,直接上【全加器】(简称FA,FullAdder)的真值表吧
| A | B | Cin | S | Cout |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
可以得到:
- S = A ⊕ B ⊕ Cin
- Cout = AB + A‘BCin + AB’Cin = AB + (A ⊕ B) Cin
电路搭起来!(下图打印错误,左上角是或门,不是异或门)
完成了加法,那减法呢?很简单,把Cin置1,并且在B前面加个非门,把它反过来就行了
时间延迟的计算:
T为单级逻辑电路的单位门延迟,与门、或门1个T,异或门3个T,总延迟为6T
- S的延迟:6T
- Cout的延迟:5T
我们把FA抽象出来,封装成一个黑盒,用一些黑 魔法把它变成一个n位的行波进位加减器(也叫串行)
- 优点:设计简单,节省器件,成本低
- 缺点:延时传递,速度慢
-
通过多加一个M控制器,走到B前面,加个异或门,也走到第一个Cin来完成控制加减法的操作
-
当前FA的Cin是上一个FA的Cout,得前一个算完,才能轮到我
时间延迟的计算:
t = 6 T + 2 T ∗ n + 3 T = ( 2 n + 9 ) T t = 6T + 2T*n + 3T = (2n + 9)T t=6T+2T∗n+3T=(2n+9)T
- 咋算的?
- 最低位的两级“异或门”时延,6T
- Cn的时延,2T*n【2T即2级与门的进位链】
- 溢出时延,3T
这个溢出的判断,就是单符号位法,只是不能判断正溢出还是负溢出
C语言模拟
加法
在模拟之前,我们先来看看大致过程,可能与上文不太相同:
4 + 5 = ?
解:[x]补 = 0 0100,[y]补 = 0 0101
异或:
0 0100
^ 0 0101
-----------
0 0001
# 异或后是无进位的结果
与:
0 0100
& 0 0101
-----------
0 0100
# 与后不为0,将结果左移1位,继续运算
=============================================
异或:
0 0001
^ 0 1000
-----------
0 1001
# 从这次开始的异或,都拿前一次异或的结果和前一次与完并移位的结果
与:
0 0001
& 0 1000
-----------
0 0000
# 与后为0,结束运算
=============================================
异或结果即结果:4 + 5 = 0100 + 0101 = 1001 = 9
代码怎么写呢?
#include 减法
一样用4-5的的例子:
4 + (-5) = ?
1 0101
解:[x]补 = 0 0100,[-y]补 = 1 1011
异或:
0 0100
^ 1 1011
-----------
1 1111
# 异或后是无进位的结果
与:
0 0100
& 1 1011
-----------
0 0000
# 与后为0,结束运算
=============================================
异或结果即结果:4 - 5 = 4 + (-5) = 0 0100 + 1 1011 = 1 1111 = -1
代码就在上面代码的基础上,稍稍封装一下:
int sub(int a,int b){
return add(a,-b);
}
我们跑一下:
xor result is:0x0001
and result is:0x0004
and left shift 1 bit:0x0008
xor result is:0x0009
and result is:0x0000
and result is 0,finished the operation!
4 + 5 = 9
----------------------------------------
xor result is:0xFFFFFFFF
and result is:0x0000
and result is 0,finished the operation!
4 - 5 = -1
硬核吧,哈哈哈哈哈哈哈哈哈
定点乘法运算
给你个式子,x=1101,y=1011,求其乘积,你怎么求?
1101(x)
* 1011(y)
----------------
1101
1101
0000
+ 1101
----------------
10001111
大概率是这么想的吧?人脑的思维模式就是这样算的,但不太适合机器:
- 假设机器是n位,那乘积就很可能是2n位
- 只有两个操作数相加的加法器,很难将n个位积一次加起来
- 多次执行“加法-移位”又太慢
那咋办呢?多亏于大规模集成电路的发展,出现了并行的流水式阵列乘法器
不带符号的阵列乘法器
我们先来看看m*n位不带符号的阵列乘法器逻辑框图(需要m乘n个与门)
实现这个过程还是比较贴合人类的思维模式的:
可能还不够清晰,我们以5位乘5位的乘法器为例:
- FA的斜向方向为进位输出
- FA的竖线方向为和输出
- 时延分析:
- ① 由n*n个与门,同时产生各FA的求和项aibj的时延:T
- ② 垂直方向,每经过一个FA有6T,到倒1层的输入:6T*(n-1)
- ③ 最后一层输入进去的异或门时延:3T
- ④ 最后一层水平方向进位传递,到最后一个FA输入:2T*(n-1)
- ⑤ 总和:(8n-4)T
带符号的阵列乘法器
提到有符,就不得不想到补码,我们可以先看一下常用的补码电路:
符号与数值分开处理,符号采用异或电路,数值采用无符号阵列乘法器:
-
原码数据可以直接运算
-
若输入为补码数据,需转换成原码后再运算
-
E = 0,不变;E = 1,求补
- 如果是原码输入,直接能用,也就不需要求补了
- 如果是补码输入,则需要求补,还原成原码计算
看倒例题:设x=-15,y=-13,用补码求x*y
[x]补 = 1 0001,[y]补 = 1 0011
解:
符号部分:xn⊕yn = 1⊕1 = 0
数值部分:|x|=1111,|y|=1101(这部是把补码还原成原码)
1111(x)
* 1101(y)
----------------
1111
0000
1111
+ 1111
----------------
11000011
因为符号位为0,所以求补输出结果也为:0 11000011
定点除法运算
原码除法
-
规则:符号与数值分开计算
- 商的符号:同号为正,异号相除为负。(可由异或实现)
- 商的数值部分由两数的绝对值相除获得。可看做是两个正数相除
-
直接上例题吧:x=0.1001,y=0.1011.求x÷y
一样,这是符合我们人脑的思维模式;但机器需要先做减法,看余数正负才知道够不够减,减下去不够减,就得恢复余数,这就有了恢复余数法,当然,也有不恢复余数法(加减交替法),根据余数符号继续往下减
除法器的设计
可控加减法单元(CAS)
这可是组成我们阵列的基本单元,FA的升级版
-
P=0,CAS做加法
-
P=1,CAS做减法
-
考虑最大的信号时延,则对于Ci的输入,Ci+1的时延为:3T
一样,做除法器也是需要牛的阵列
-
2n位除以n位的不恢复余数阵列除法器,含有(n+1)^2 个CAS单元。
-
考虑最大信号延迟,除法执行时间为: 3(n+1)^2*T
当然啦,这个不是重点,重点是它的组成结构——不恢复余数除法器
恢复余数除法器
虽然不是重点,但我们也先说一下,有个对比先
大致流程:
-
通过减法依次比较被除数和除数,判定商;若不够减,则通过回加余数恢复
-
缺点:控制复杂
-
运算要求
- 确保参与运算的均是纯小数, 且被除数小于除数
- 被除数数值位扩充为除数数值位2倍
具体例子不说了,直接上重点
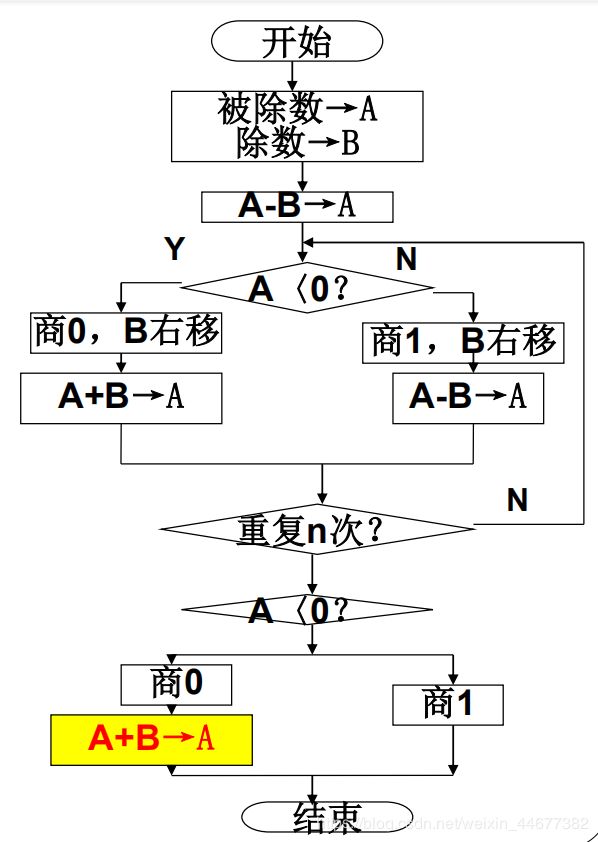
不恢复余数除法器
流程如下:
-
不恢复余数法
- 通过减法依次比较被除数和除数,判定商。
- 若不够减,不恢复余数,而根据余数的符号决定下一步操作
- 最后一步的操作特殊处理,若商为0要恢复余数
- 也称为加减交替法
-
注意
- 被除数(数值部分,即尾数)长度= 2*除数长度
- 送入不恢复余数阵列除法器计算时,必有被除数<除数。若原始数据不满足,则通过比例因子进行处理。
这样一来,降低了控制的复杂程度
光说没内味,直接上例题吧!
【例题】x=0.101001, y=0.111, 求q = x÷y
解:
[x]补=0.101001,[y]补=0.111 ,[-y]补=1.001
0.101001 ;被除数x
+[-y] 1.001 ;第一步减除数y
---------------------------
1.110001 <0 q4=0 ;余数为负,商0,下步做加法
+[y] 0.0111 ;除数右移1位加(正0)
---------------------------
0.001101 >0 q3=1 ;余数为正,商1,下步做减法
+[-y] 1.11001 ;除数右移1位减(负1)
---------------------------
1.111111 <0 q2=0 ;余数为负,商0,下步做加法
+[y] 0.000111 ;除数右移1位加(正0)
---------------------------
0.000110 >0 q1=1 ;余数为正,商1,直接结束
商:q = q4.q3q2q1 = 0.101
余数:r = 0.000110
C语言模拟
乘法
int mul(int a,int b){
int i,res=0;
int flag;
// if the result is positive
if(a>0 && b>0 || a<0 && b<0){
flag = 1;
}else{
flag = 0;
}
a = abs(a);
b = abs(b);
for(i=0;i<b;i++){
res = add(res,a);
}
if(flag)
return res;
else
return -res;
}
除法
int div(int a,int b){
int i,count,res,quotient=0;
int flag;
// if the result is positive
if(a>0 && b>0 || a<0 && b<0){
flag = 1;
}else{
flag = 0;
}
a = abs(a);
b = abs(b);
res = a;
while(sub(res,b)>0){
res = sub(res,b);
quotient++;
}
if(flag)
return quotient;
else
return -quotient;
}
一些小练习
- X=-1100, Y=-1000,则X+Y的结果用变形补码可表示为(),其中符号位为(),说明()(有/无)溢出 。
解:[x]补 = 11 0100,[y]补 = 11 1000
11 0100
+ 11 1000
------------
10 1100
∴ x + y = 10 1100,符号位为10,有溢出(负溢出)
- Y=-10001,在字长为8位的机器中,[-Y]的补码为()。
解:
[Y]原 = 1 10001
[-Y]原 = 0 10001
[-Y]补 = 0 10001 = 0001 0001
- 实现8位*8位的不带符号阵列乘法器,共需要()个全加器,()个与门。
FA:8 * (8-1) = 56
与门:8 * 8 = 64
- X=11000,Y = -11111,请用不恢复余数除法计算X÷Y,写出完整的解题过程。
提示:
①先将X和Y转换为纯小数;
②符号位和数值部分分开计算,仅将X和Y的绝对值部分(正数)按流程计算
解:
x = 0.11000*2^5, y = -0.11111*2^5, 相互抵消一下,其实就没了
这边我们暂时把x和y的2^5去掉,负号也暂时先放一边
[x]补=0.11000 00000,[y]补=0.11111 ,[-y]补=1.00001
0.1100000000 ;被除数x
+[-y] 1.00001 ;第一步减除数y
---------------------------
1.1100100000 <0 q6=0;余数为负,商0,下步做加法
+[y] 0.011111 ;除数右移1位加(正0)
---------------------------
0.0100010000 >0 q5=1;余数为正,商1,下步做减法
+[-y] 1.1100001 ;除数右移1位减(负1)
---------------------------
0.0000011000 >0 q4=1;余数为正,商1,下步做减法
+[-y] 1.11100001 ;除数右移1位减(负1)
---------------------------
1.1110011100 <0 q3=0;余数为负,商0,下步做加法
+[y] 0.000011111 ;除数右移1位加(正0)
---------------------------
1.1111011010 <0 q2=0;余数为负,商0,下步做加法
+[y] 0.0000011111 ;除数右移1位加(正0)
---------------------------
1.1111111001 <0 q1=0;最后一位商为0,要恢复余数
+[y] 0.0000011111 ;恢复余数时,均+[y]补
---------------------------
0.0000011000
商:q = -q6.q5q4q3q2q1 = -0.11000
余数:r = 0.0000011000 * 2^5 = 0.11000