红黑树 B树 B+树
红黑树
假设1-100个数字 让你猜 根据提示告诉你打了还是小了
想到的算法肯定是二分查找
如果转成数据结构 有哪些?
二叉树 二分查找树
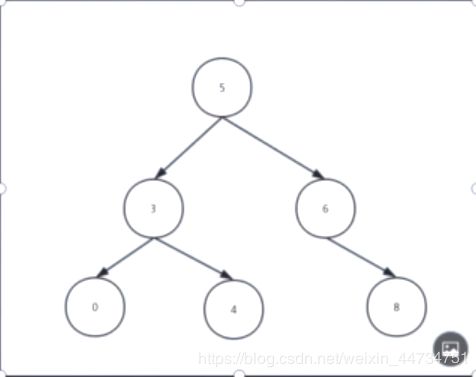
由一组数{0.3.4.5.6.8}
时间复杂度就是树的深度 logn
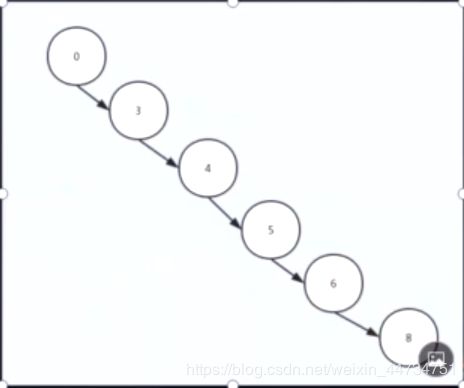
这个树经过增删操作可能变成这样:
虽然是一棵树 但本质上变成了链表 时间复杂度变成了O(n)
平衡二叉树
我们要改造这个树 改造成平衡二叉树(追求极致的平衡)
那么有了平衡二叉树为什么还要有红黑树呢?
平衡二叉树追求极致平衡 每次增删都会影响高度差 每次就要调整树结构
影响性能 所以引入红黑树 ;
红黑树
(特殊的二叉树)二叉查找树
红黑树 追求局平衡
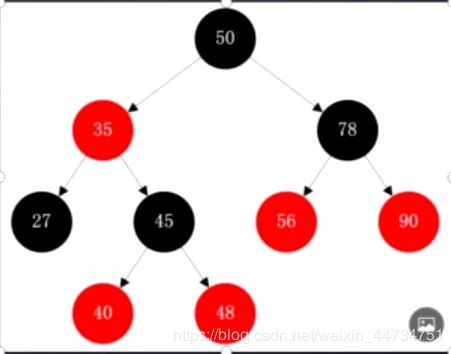
红黑树的性质
1每个节点不是红色就是黑色
2不可能有连在一起的红色结点
3根节点都是黑色
4每个红色节点的俩个子节点都是黑色 叶子节点都是黑色的
5每次增加的节点都是红色(保证不会变成链表)
只要二叉树满足这几个特点 就不会会变成链表
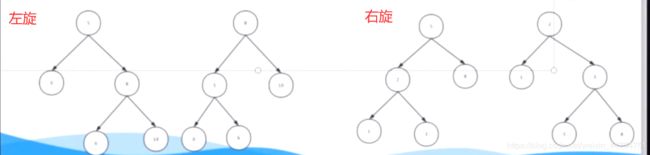
左旋和右旋
旋转和变换的插入规则 : 插入的节点一定是红色 因为红黑树可能是全黑色 插入红色 才会有变化
红黑树中插入节点
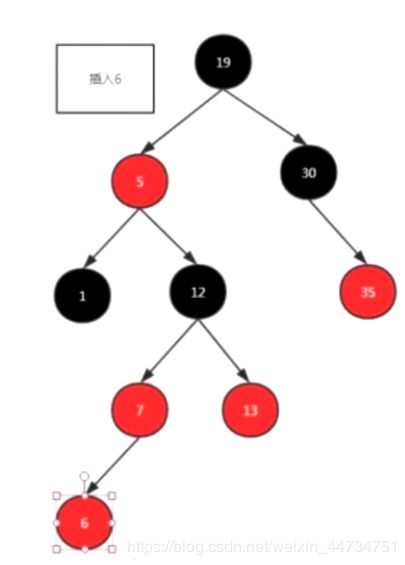
提前声明 这个树的结构代表了红黑树的各种情况
我们想在这个树中插入6
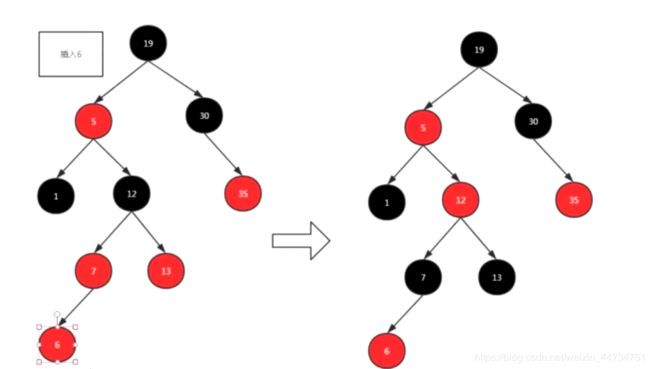
2-根据二叉查找树的规则插入6插入之后 红色连到了一起 不满足红黑树性质 所有要利用旋转和变换
上面面这个图使用变颜色的方式:为什么? 变颜色有个前提
如果当前节点的父亲是红色 且他的爷爷节点的另一个子节点(叔叔节点)也是红色(13)就要用下面的规则
1父节点设为黑色
2叔叔节点设为黑色
3把父亲的父亲设为红色
4指针定位到爷爷身上
变换颜色之后发现还是不满足 5和12都为红色连在了一起 这时候就要用的左旋 因为12是右子树 所以左旋
左旋是当前节点(12) 和父节点(5) 这俩旋转
左旋前提;
指针指向的元素(12) 的父节点是红色,且叔叔是黑色,且指针指向的元素是右子树 那么我们以父节点左旋

左旋之后 12和5都为红色连到了一起 还是不满足
使用右旋
为什么 因为5是左子树 所以右旋
右旋 :不是当前节点和父节点旋转 而是父节点和爷爷节点旋转
前提 :当前节点的父节点是红色 爷爷节点是黑色 当前节点是左子树
步骤
1旋转之前把父节点变为黑色
2旋转之前把爷爷节点变为红色
java实现插入和左旋
package com.test;
public class RedBlackTree {
//定义颜色
private final int R = 0;
private final int B =1;
private Node root =null;
class Node{
/*
每个节点的内容:
1数据
2左子节点
3右子节点
4父节点
5颜色
*/
int data;
int color = R;
Node left;
Node right;
Node parent;
public Node(int data){
this.data=data;
}
}
//插入节点
public void insert(Node root , int data){
if(root.data<data){
if(root.right!=null) {
root.right = new Node(data);
}else {
insert(root.right , data);
}
}else{
if(root.left!=null){
root.left=new Node(data);
}else{
insert(root.left,data);
}
}
}
//左旋
public void leftRotate(Node node){
if(node.parent==null){
Node E =root;
Node S =E.right;
E.right=S.left;
E.parent=S;
S.parent=null;
}
else{
if(node==node.parent.left){
node.parent.left=node.right;
}else{
node.parent.right=node.right;
}
node.right=node.right.left;
node.right.left.parent=node;
node.right.parent=node.parent;
node.parent=node.right;
node.parent.left=node;
}
}
}
能做索引的数据结构有哪些?
数组,链表,哈希 红黑树 B树(b,b+)
hash表不能作为mysql存储的原因
mysql不能用哈希结构为什么?
哈希函数会计算出一个hash值
select * from user where id =100;
hash(100)=key 根据id算出一个哈希值
如果sql语句变成 select * from user where id<100 and id>50;
哈希值就没用了 不支持范围查找 和部分信息查找
我们看下面这俩条语句
1: select * from user where id=100 and name=“ZS;
2:select * from user where id =100;
这俩条语句查出来的东西一样 但是如果用哈希
hash(100)=key
hash(100+“zs”)=key 算出来的hash值是不一样的
所以也不支持部分查询
综上 不支持部分查找也不支持范围查找 而且还有hash冲突问题
什么情况下可以使用hash呢 ?没有范围查询和部分查询 查询条件不会变
红黑树表不能作为mysql存储的原因
树太高 读取次数过多 而且 读取浪费
为什么能作为hashmap的底层呢 因为在内存中 new hasmap()
使用n叉数 一层有很多个节点 降低了树的高度 一次读取很多节点 解决了读取浪费 这个就叫B树
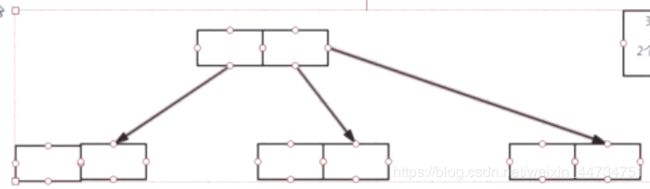
B树
M阶的BTree特性:
1节点最多含有m个子树 每个节点能存m-1条数据
2如果跟节点不是叶子节点 则至少有俩个子树 (如果有子节点肯定分裂了 分裂至少有俩个)
3除根节点和叶子节点 其他节点至少有ceil(m/2)个子节点(子树)分裂的时候从中间分开
当B树不满足上面的条件会怎样 分裂? 红黑树已经知道了 是左右旋变颜色
BTree 分裂
B树为什么没成为mysql最终的存储结构?
1如果查询id小于13的 还是会便利 左子树 这样索引会失效
2每个节点存储的是 索引+数据 学过设计模式都知道 单一原则 存储俩个东西 稳定性下降
所以引入了B+树作为最终数据结构
B+树
观察B+树与b树的图发现三个区别
1叶子节点连起来了
2非叶子节点不存数据
3数据和节点一样多
特点1是 双向链表解 这样就决了范围查询 比如查找小于9的id 定位到叶子结点之后 左面的都是小于9的而且是有序的