2018～2019初赛复习整理

---

讲义

初赛复习讲义和真题讲解：传送门
组合数学：传送门

---

排序算法讲解

讲义

博客园的博客
快速排序的三种实现
内部排序和外部排序

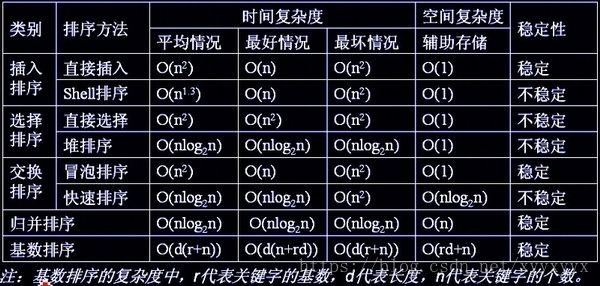
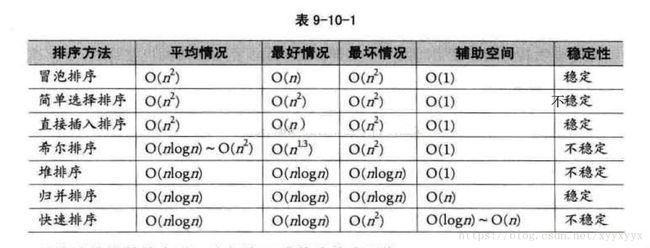
贺来的图和tips

有关快速排序的辅助空间以下图为准。

tips:

1. 关于快速排序的辅助存储空间：递归每层一个，O(logn)~O(n)。
2. 关于希尔排序：时间复杂度平均O(n^1.3)，到不了O(nlog2n)，但是比普通的插入排序快，依赖于增量的选取，倒序时最坏。是一个就地排序，辅助空间O(1)。是不稳定排序
3. 希尔排序具体实现：选一个步长h，对于$i,i+h,i+h\ast 2,i+h\ast 3$…做插入排序，然后减小增量，最后一遍增量为1，等于做普通的插入排序。
4. 基数排序：稳定排序，时间空间O(n)，但依赖于数据值的大小。

e.g.

16、下列排序算法中，哪些排序是不稳定的（）。
A、快速排序 B、选择排序
C、基数排序 D、希尔排序

ans=ABD

12、下列关于排序说法正确的是（）。
A、 插入排序、冒泡排序是稳定的
B、 选择排序的时间复杂度为O(n^2)
C、 选择排序、希尔排序、快速排序、堆排序是不稳定的
D、 希尔排序、快速排序、堆排序的时间复杂度为O(nlogn)

ans=ABC

基于比较的排序算法最小时间复杂度

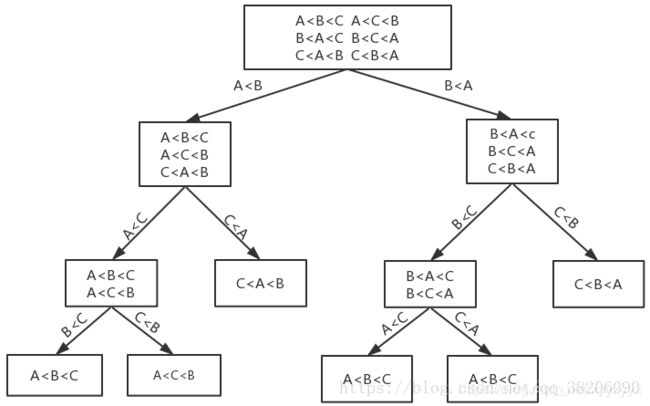
用判定树证明

blog

叶子有$n!$个，树高${\log }_2(n!)={\log }_2(n)+{\log }_2(n-1)+...+lo{g}_2(1)<n{\log }_{2}n$

图：

e.g.

17、下列关于排序的算法，不正确的是（）。
A.不存在这样一个基于排序码比较的算法：它只通过不超过9次排序码的比较，就可以对任何6个排序码互异的数据对象实现排序。
B.如果输入序列已经排好序，快速排序算法将比归并排序更快。
C.希尔排序的最后一趟就是冒泡排序。
D.任何基于排序码比较的算法，对n个数据对象进行排序时，最坏情况下的时间复杂度不会低于O(nlogn)。

ans=BC

解析：希尔排序的最后一趟是插入排序。

---

Hash

处理冲突

1. 开放寻址法：线性探测，二次探测（0，右1，左1，右2，左2，右4，左4…），伪随机探测
2. 再哈希法：重复时使用不同的Hash函数再计算哈希值
3. 链表法
4. 建立公共溢出区：只要重复的就放到一个线性表里面，查询的时候先找哈希表，没找到再遍历线性表

e.g.

设有一个含有13个元素的Hash表（0-12），Hash函数是：H(key)=key%13，其中%是求余数运算。用二次探查法解决冲突，则对于序列(8,31,20,33,18,53,27)，则下列说法正确的是（）。
A、18在4号格子中 B、33在6号格子中
C、31在5号格子中 D、20在7号格子中

ans=ABCD

平均查找长度

1. 成功平均查找长度
   ans = (表中每个元素在插入时再散列的次数+元素个数)/元素个数
   tips:没有再散列就是1
2. 不成功平均查找长度
   ans = 表中每个位置再散列查找到第一个空位的次数/表长
   tips:表长是指0~MOD-1，因为有的题哈希数组可能会比MOD开得大，导致有的数再散列会超过MOD。

e.g.

7、设哈希函数H（K）=3 K mod 11，哈希地址空间为0～10，对关键字序列（32，13，49，24，38，21，4，12），按线性探测法解决冲突的方法构造哈希表，求出等概率下查找失败时的平均查找长度（）。
A. 11/11 B. 29/11
C. 35/11 D. 40/11

ans=D

---

基础数据结构

堆

关于O(n)建堆

大致思路是先把所有数随便在堆里放好，然后从下往上，每个点的左右子树已经是堆了，就把这个点和左右儿子的堆合并，复杂度$O(\log h)$，h是当前点到叶子的距离。因为是$O(\log h)$而不是$O(\log n)$，所以是一个差比数列求和得到$O(n)$而不是看起来的$O(n\log n)$。

下面是证明：

假设堆的大小为$n$，高度为$h=\log n$

那么复杂度就是

$$T(n)=\sum _{i=0}^{h-1}(h-i)\ast 2^i=2^0\ast h+2^1\ast (h-1)+...+2^{h-1}\ast 1$$

$$2T(n)=\sum _{i=0}^{h-1}(h-i)\ast 2^{i+1}=2^1\ast h+2^2\ast (h-1)+...+2^h\ast 1$$

下面减上面，得到

$$T(n)=2^h-h+(2^1+2^2+...+2^{h-1})=O(2^h)=O(n)$$

常数是2多一点。

看两道题，假如不知道O(n)建堆的话简直**

e.g.

读程序写结果

#include  
using namespace std;  
int n=12;  
char ch[]= {'q','A','S','O','R','T','E','X','A','M','P','L','E'};  
void shift(int k,int n) {  
	char v;  
	int j;  
	v=ch[k];  
	j=k+k;  
	while(j<=n) {  
		if(j<n&&ch[j]<ch[j+1])  
			j++;  
		if(v<ch[j]) {  
			ch[j/2]=ch[j];  
			j*=2;  
		} else  
			return;  
		ch[j/2]=v;  
	}  
}  
void hpsrt() {  
	int k;  
	char tmp;  
	for(k=n/2; k>0; k--)  
		shift(k,n);  
	cout<<"No.1:";  
	for(k=1; k<=n; k++)  
		cout<<ch[k];  
                cout<<' ';  
	for(k=n; k>0; k--) {  
		tmp=ch[1];  
		ch[1]=ch[k];  
		ch[k]=tmp;  
		shift(1,k-1);  
	}  
}  
int main() {  
	int k;  
	hpsrt();  
	cout<<"No.2:";  
	for(k=1; k<=n; k++)  
		cout<<ch[k];  
	cout<<endl;  
	return 0;  
}

ans=No.1:XTORSEAAMPLE No.2:AAEELMOPRSTX

解析：就是O(n)建堆，再一个一个从堆里取出来从小到大排序。注意是大根堆并且ch[0]='q’并不用管。

e.g.

已知T(n) = 2*T(n/2) + O(lg n)
求T(n)时间复杂度（ ）。
A．O (n2) B．O (n logn ) C．O (n) D． O (1)

ans=C

解析：就是建堆的复杂度。然而用主定理并推不出来。

树

哈夫曼树

不知道为什么要放在这里，但好像没地方放了。

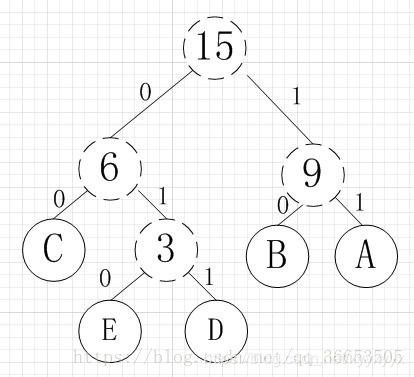
1. 结构：哈弗曼树是一棵二叉树，一个点向左右儿子连的边分别有边权0和1，一条从根到叶子的路径表示一种字符。如下图。
2. 性质：是一种无前缀编码，解码时不会混淆。每种字符的编码长度为叶子的深度。最优的编码方式会将出现次数多（出现概率大）的字符放在深度较浅的位置。

图来自这篇博客

e.g.

13.现有一段文言文，要通过二进制哈夫曼编码进行压缩。简单起见，假设这段文言文只由4个汉字“之”、“乎”、“者”、“也”组成，它们出现的次数分别为700、600、300、400。那么，“也”字的编码长度可能是（ ）。
A．1或2 B．2或3 C．3或4 D．1或3

ans=B

解析：
可能是一棵深度为2的完全二叉树，或者一棵深度为3的非叶子节点连成一条链的树。

---

膜拜CCF

NOI：全国青少年信息学奥林匹克，1984年开始。自1999年开始，NOI期间，举办同步夏令营和NOI网上同步赛。

NOIP：全国青少年信息学奥林匹克联赛(National Olympiad in Informatics in Provinces简称NOIP)自1995年开始，2019凉凉。

冬令营：全国青少年信息学奥林匹克冬令营(简称冬令营)，自1995年起。

APIO: 亚洲与太平洋地区信息学奥赛（Asia Pacific Informatics Olympiad）简称（APIO）2007年创建，该竞赛为区域性的网上准同步赛，是亚洲和太平洋地区每年一次的国际性赛事。

选拔赛：选拔参加国际信息学奥林匹克中国代表队的竞赛（简称选拔赛）。2018年以前叫CTSC，现在叫CTS。

IOI： 出国参加国际信息学奥林匹克竞赛（International Olympiad in Informatics）简称（IOI）。自1989年开始，我国组织参加国际信息学奥林匹克（IOI）竞赛。

CSP-J/S：CCF非专业级软件能力认证(Certified Software Professional Junior/Senior，简称CSP-J/S)创办于2019年，是由CCF统一组织的评价计算机非专业人士算法和编程能力的活动。

---

计算机基础知识

原码反码和补码

计算：

1. 非负数不变
2. 负数：反码为除符号位之外取反，补码为反码+1

反码是为了解决正负数直接相加的问题，补码则是为了解决-0的问题。

拓展：

1. 正负数位运算
2. 浮点数的反码补码

e.g.

2、十进制数3 ^ (-2)的位运算结果为（）。
A、-3（十） B、1（十） C、1/9（十） D、-2（十）

ans=A

e.g.2

11、二进制小数-0.1011的补码为（）。
A、1.1011 B、1.0101 C、10.0101 D、11.0101

ans=B

解析：
浮点数的存储后面有。所以阶码不用管，只要管尾数取补码就好了。

停机问题

停机问题本质是一高阶逻辑的不自恰性和不完备性，与理发师悖论类似。

不存在一个程序能够判断任意一个程序能否在有限时间内结束运行。

证明：

反证法。

假设存在$P(H,I)$能够判断任意一个$H$能否在输入为$I$时在有限时间内结束运行。

构造一个$Q(X)$如下

function Q(X)
{
	if (P(X,X)==停机){
		while(1){} // 死循环
	}
	else return 停机
}

那么$P(Q,Q)$就会产生悖论。所以$P$无法满足要求。

e.g.

10、一个无法靠自身的控制终止的循环称为“死循环”，例如，在C语言程序中，语句“while(1) printf(“”);”就是一个死循环，运行时它将无休止地打印号。下面关于死循环的说法中，只有（）是正确的。
A、不存在一种算法，对任何一个程序及相应的输入数据，都可以判断是否会出现死循环，因而，任何编译系统都不做死循环检验。
B、有些编译系统可以检测出死循环。
C、死循环属于语法错误，既然编译系统能检查各种语法错误，当然也应该能检查出死循环。
D、死循环与多进程中出现的“死锁”差不多，而死锁是可以检测的，因而，死循环也可以检测的。

ans=A

信息论之父

香农
p.s.计算机之父－－冯诺依曼（详见冯诺依曼理论）

摩尔定律

是由英特尔（Intel）创始人之一戈登·摩尔（Gordon Moore）提出来的。其内容为：当价格不变时，集成电路上可容纳的元器件的数目，约每隔18-24个月便会增加一倍，性能也将提升一倍。

现已经放缓至约三年翻一番。

冯诺依曼理论：

1、计算机硬件设备由存储器、运算器、控制器、输入设备和输出设备5部分组成。
2、存储程序思想——把计算过程描述为由许多命令按一定顺序组成的程序，然后把程序和数据一起输入计算机，计算机对已存入的程序和数据处理后，输出结果。
美籍匈牙利科学家冯·诺依曼最先提出程序存储的思想，并成功将其运用在计算机的设计之中，根据这一原理制造的计算机被称为冯·诺依曼结构计算机，由于他对现代计算机技术的突出贡献，因此冯·诺依曼又被称为“计算机之父”。

e.g.

12、下列属于冯诺依曼计算机模型的核心思想有（）。
A、采用二进制表示数据和指令 B、采用“存储程序”工作方式
C、计算机硬件有五大部件（运算器、控制器、存储器、输入和输出设备）
D、结构化程序设计方法

ans=ABC，与程序设计无关

第一个程序媛：

阿达·洛芙莱斯（Ada Lovelace），解伯努利方程，建立循环和子程序概念

CPU：Central Proccessing Unit

性能指标：字长、主频（register寄存器：CPU的组成部分，速度最快）
第一块4位微处理器intel 4004

系统程序–数据库系统

• Keywords：database,DB,base…

传送到百度百科
Foxpro，Access，Oracle，Sybase，DB2和Informix则是数据库系统。

存储器：

内存（速度由小到大排序）：ROM（只读，装入整机前写好并不能更改），RAM（用来暂时存储程序、数据和中间结果），cache（高速缓冲存储器），寄存器
外存：硬盘，闪存（又名优盘。。。）
显存：显卡内存，是暂时存储图像信息类似内存的存在

问：BIOS在哪里？

答：在ROM。

e.g.

12.下列说法中，正确的是（ ）。
A）数据总线决定了中央处理器CPU所能访问的最大内存空间的大小。
B）中央处理器CPU内部有寄存器组，用来储存数据。
C）不同厂家生产的CPU所能处理的指令集是相同的。
D）数据传输过程中可能会出错，奇偶校验法可以检测出数据中那一位在传输中出了差错。

ans=B

解析：
B 寄存器上面有累加器，但是不妨碍他的存储功能呀。。。
D 不能知道具体是哪一位，只能知道有没有错。

字符的存储：

1.ASCII码（American Standard Code for Information Interchange）：一个字节，0x00~0x7f。0 ~33控制字符，33之后可见（48-'0’，65-‘A’，97-‘a’）
2.汉字：两个字节，每个0x80~0xff。国标码，处理码，输出码

其他存储

图片存储：（24/32位真彩色）颜色位数×图片大小
视频存储：图片容量×帧频×时间
音频存储：频率×量化位数×时间×声道数（bit）

计算机语言：

1. 机器语言
2. 汇编语言（assembly language）：是一种用于电子计算机、微处理器、微控制器或其他可编程器件的低级语言，亦称为符号语言。在汇编语言中，用助记符代替机器指令的操作码，用地址符号或标号代替指令或操作数的地址。在不同的设备中，汇编语言对应着不同的机器语言指令集，通过汇编过程转换成机器指令。特定的汇编语言和特定的机器语言指令集是一一对应的，不同平台之间不可直接移植。
3. 高级语言：源程序->可执行程序的方式：1编译（pascal，c++，c）2解释（Java，Python，VB）
   #类的要领和继承：simula67
4. 面向过程和面向对象：面向过程就是分析并写出解决问题所需要的步骤。面向对象是把构成问题事务分解成各个对象，建立对象的目的不是为了完成一个步骤，而是为了描叙某个事物在整个解决问题的步骤中的行为。博客
   面向对象：simula67（第一个），smalltalk（第一个支持动态类型），VC++，C#，JAVA，delphi，PHP
   面向过程：c，Fortran（科学计算）
5. 解释语言和编译语言：解释语言将源文件解释成可执行文件，编译语言先将源文件编译成目标程序，然后再经过连接程序变成可执行文件。Python,Java是解释语言，C++,Pascal是编译语言。

• 编译程序过程：源代码 (source code) → 预处理器 (preprocessor) → 编译器 (compiler) → 目标代码 (object code) → 链接器 (Linker) → 可执行程序 (executables)
• 编译器的作用：翻译，产生目标程序。
• 编译程序的速度一般比解释程序的快。

6. 脚本语言：某某script，如JavaScript，是一种解释语言。
7. 函数式编程：（贺自百度）函数式编程是种编程方式，它将电脑运算视为函数的计算。函数编程语言最重要的基础是λ演算（lambda calculus），而且λ演算的函数可以接受函数当作输入（参数）和输出（返回值）。和指令式编程相比，函数式编程强调函数的计算比指令的执行重要。和过程化编程相比，函数式编程里函数的计算可随时调用。

e.g.

1.以下关于编程语言的选项中，正确的是（ ）
A.操作系统控制和管理软硬件资源，需要直接操作机器，所以需要用机器语言编写
B.同样一段高级语言程序通过不同的编译器可能产生不同的可执行程序
C.C++是一种纯面向对象语言
D.解释执行的语言只能选择一个解释器。

ans=B

操作码和操作数

是机器语言的术语。

操作码指计算机程序中所规定的要执行操作的那一部分指令或字段(通常用代码表示)，其实就是指令序列号，用来告诉CPU需要执行哪一条指令。

操作数是运算符作用于的实体，是表达式中的一个组成部分，它规定了指令中进行数字运算的量 。表达式是操作数与操作符（码）的组合。

双操作数又称为源操作数（source）和目的操作数（destination）。

e.g.

6.计算机能直接执行的指令包括两部分，它们是（ ）
A.源操作数与目标操作数 B. 操作码与操作数
C.ASCII码与汉字代码 D. 数字与字符

ans=B（看过就会了）

浮点数存储

了解尾数、基数、阶码存储
传送到博客

计算机性能标准之字长

字长是用来表示一次性处理事务的一个固定长度的位（bit）的位数

系统总线

虽然系统总线于1970年代至1980年代广受欢迎，但是现代的计算机却使用不同的分离总线来做更多特定需求用途。

系统总线上传送的信息包括数据信息、地址信息、控制信息，因此，系统总线包含有三种不同功能的总线，即数据总线DB（Data Bus）、地址总线AB（Address Bus）和控制总线CB（Control Bus）。

e.g.

8.计算机系统总线上传送的信号有（ ）
A. 地址有信号与控制信号 B. 数据信号、控制信号与地址信号
C. 控制信号与数据信号 D. 数据信号与地址信号

ans=B

---

计算机网络

1. 分类

地理范围：局域网（LAN，Local Area Net），城域网（MAN，Metropolitan），广域网（WAN，Wide）

p.s.以太网是一种局域网

e.g.

1. 以下属于无线通信技术的有（ ）。
   A. 蓝牙 B. WiFi C. GPRS D. 以太网

ans=ABC

解析：
GPRS（General Packet Radio Service）
以太网是目前应用最普遍的局域网技术（有线）

2. 协议

1. http(s)-超文本传输协议（安全）[HyperText Transfer Protocol ( safe ) ]
2. ftp-文件传输协议[File Transfer Protocol]
3. smtp/pop3-用于邮件传输（前者发，后者收）[Simple Mail Transfer Protocol/Post Office Protocol-Version 3]
4. IPX-数据包交换[Internet work Packet Exchange]

plus.html-超文本标记语言[HyperText Markup Language]

3. TCP/IP（Transmission Control Protocol/Internet Protocol）协议

4. ISO（International Organization for Standardization）的OSI（Open System Interconnection）七层模型

与TCP/IP的关系

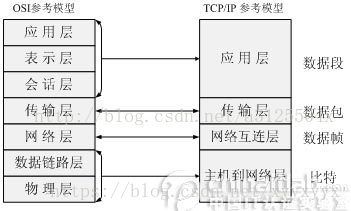
各种协议所处阶层

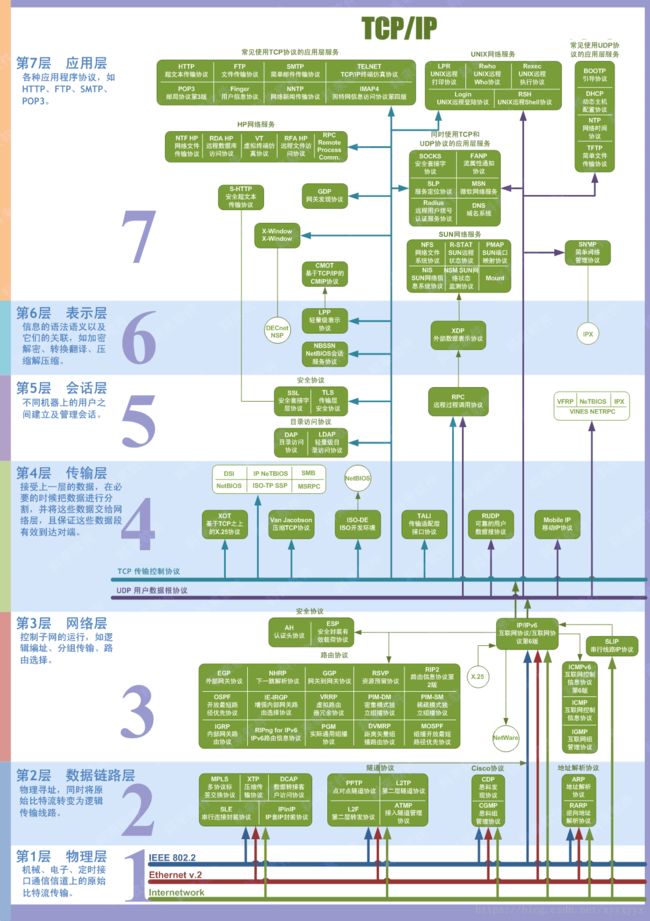
简化版

重点：TCP协议在传输层（从下到上第4层），IP协议在网络层（从下到上第3层）

5. IP地址：

比较不错的博客

看图，根据32位前端连续1的个数来区分。

也就是说，分为以下几类：
A: 0.0.0.0-127.255.255，其中段0和127不可用
B: 128.0.0.0-191.255.255.255
C: 192.0.0.0-223.255.255.255
D: 224.0.0.0-239.255.255.255
E: 240.0.0.0-255.255.255.255，其中段255不可用
这其中除了段0和段127之外，还有一些IP地址因为有其他的用途，是不可以用作普通IP的。还有一部分被用作私有IP地址。

6.ipv4和ipv6

ipv4是32位（4*8），ipv6是128位。

7.服务

Internet提供了以下4种服务：

1.Internet上提供了高级浏览WWW服务

WWW(World Wide Web)服务是一种建立在超文本基础上的浏览、查询因特网信息的方式，它以交互方式查询并且访问存放于远程计算机的信息，为多种因特网浏览与检索访问提供一个单独一致的访问机制。Web 页将文本、超媒体、图形和声音结合在一起。因特网给企业带来通信与获取信息资源的便利条件。

2.Internet上提供了电子邮件E-mail服务

3.Internet上提供了远程登录Telnet服务

Telnet协议是TCP/IP协议族中的一员，是Internet远程登陆服务的标准协议和主要方式。它为用户提供了在本地计算机上完成远程主机工作的能力。

4.Internet上提供了文件传输FTP服务

FTP 是File Transfer Protocol（文件传输协议）的英文简称，而中文简称为“文传协议”。

8.域名

百度百科说：

域名（英语：Domain Name），简称域名、网域，是由一串用点分隔的名字组成的Internet上某一台计算机或计算机组的名称，用于在数据传输时标识计算机的电子方位（有时也指地理位置）。

网域名称系统（DNS，Domain Name System，将域名和IP地址相互映射的一个分布式数据库）是因特网的一项核心服务，它作为可以将域名和IP地址相互映射的一个分布式数据库，能够使人更方便地访问互联网，而不用去记住能够被机器直接读取的IP地址数串。

简单说域名就是IP地址的别名，DNS就是一个在IP和域名之间映射的函数。

e.g.

6.关于计算机网络，下面的说法哪些是正确的：
A)网络协议之所以有很多层主要是由于新技术需要兼容过去老的实现方案。
B)新一代互联网使用的IPv6标准是IPv5标准的升级与补充。
C)TCP/IP是互联网的基础协议簇，包含有TCP和IP等网络与传输层的通讯协议。
D)互联网上每一台入网主机通常都需要使用一个唯一的IP地址，否则就必须注册一个固定的域名来标明其地址。

ans=C

解析：
A 显然是有实用的目的的。比如灵活性好，易于维护。
B IPV4
D “否则”错了，IP地址是必须的，而域名不是必须的。

9.设备

基本的网络设备有：计算机（无论其为个人电脑或服务器）、集线器、交换机、网桥、路由器、网关、网络接口卡（NIC）、无线接入点（WAP）、打印机和调制解调器、光纤收发器、光缆等。

e.g.

2. 可以将单个计算机接入到计算机网络中的网络接入通讯设备有（ ）。
   A. 网卡 B. 光驱 C. 鼠标 D. 显卡

ans=A

解析：
光驱，disk driver，光盘驱动，电脑用来读写光碟内容的机器

---

C++

switch语句

平常根本不用的说，都不知道他有什么存在的意义。。。

先看一道毒瘤题：

#include
using namespace std;
int main() {
	int a,k;
	a=5;
	k=8;
	char l='a';
	while(a>0) {
		switch(l+=a--) {
			case 'j':
			case 'l':
				l-=a;
			case 'f':
				a--;
				continue;
			case 'm':
			case 'p':
				l++;
				break;
			default:
				k++;
			case 'o':
				k-=2;
				continue;
		}
		k++;
		l--;
	}
	cout<<l<<k<<endl;
	return 0;
}

1.程序输出为（）
A. r6 B. l6 C. k8 D.i12

2.如果第一个continue改为break了，答案为i8是否正确？（）。
A. 正确 B. 错误

想要做此题，就有必要知道switch的运作方式。

大致如下：

1. 对于每一个case的常量，与switch的值比较，不相等则跳过这个case继续比较，相等则进入2。
2. 执行这个case开始到switch结束的所有语句，除非有break退出了switch。

注意：

1. 退出switch只能用break，与continue无关。上面程序的continue是针对while循环而并非用来跳出switch。

知道continue和break的用处，就可以轻松地做这题了。

答案是B; B。第二题的正确输出应该是h9。

字符串

18、以下程序的输出结果是（ ）

int main(){
	char st[20]= "hello\0\t\\";
	printf("%d %d \n",strlen(st),sizeof(st));
} 

A.12 20 B. 5 20 C. 20 20 D. 5 5

注意\0是char数组的结尾符号，所以在算strlen的时候到\0就结束了。

p.s.\\表示一个斜杠，如果单独的\是会报错的。

指针、地址和引用

上一个程序

#include
#include
#include
using namespace std;

void fun1(int *x, int *y) // 交换两个参数指针，但是不影响函数外面的值
{
    int *k;
    k = x;
    x = y;
    y = k;
}

void fun2(int *x, int *y) // 相当于引用，交换两个参数指针所指的值
{
    int k;
    k = *x;
    *x = *y;
    *y = k;
}

void fun3(int &x, int &y) // 引用，x和y是int类型而不是*int
{
    int k;
    k = x;
    x = y;
    y = k;
}

void fun4(int *x, int *y) // 等于fun2()
{
    int *k;
    k = new int;
    *k = *x;
    *x = *y;
    *y = *k;
}

int &fun5() // fun5()的返回值引用了xa，所以修改fun5()就修改了xa，并且静态变量xa会保持之前修改过的值
{           // 这里static不能去掉，去掉就会warning，因为一般局部变量在退出函数的时候是会清除的
    static int xa = 10;
    return xa;
}

int main()
{
    int a = 233, b = 666;
    int *x1 = &a, *y1 = &b;
    int &x3 = a, &x4 = b; // 引用

    fun1(x1, y1);
    cout << a << " " << b << endl;
    cout << *x1 << " " << *y1 << endl;
    cout << "----------------------------" << endl;

    fun2(x1, y1);
    cout << a << " " << b << endl;
    cout << *x1 << " " << *y1 << endl;
    cout << "----------------------------" << endl;

    fun3(a, b);
    cout << a << " " << b << endl;
    cout << *x1 << " " << *y1 << endl;
    cout << "----------------------------" << endl;

    fun4(x1, y1);
    cout << a << " " << b << endl;
    cout << *x1 << " " << *y1 << endl;
    cout << "----------------------------" << endl;

    cout << fun5() << endl;
    fun5() = 30;
    cout << fun5() << endl;
    return 0;
}
/*
输出：
233 666
233 666
----------------------------
666 233
666 233
----------------------------
233 666
233 666
----------------------------
666 233
666 233
----------------------------
10
30

*/

运算符优先级

如何方便地记住优先级：

1. 首先，单目运算符优于双目优于三目。
2. 在双目运算符中，四则运算和左移右移最高，然后是比较运算符，然后是位运算，然后是逻辑运算符。
3. 再细分的话，四则运算优于移位，等于和不等于在比较运算符中优先级低，位运算"&" 优先于 “^” 优先于 “|” ，逻辑运算"&&" 优先于 “||”

容易记错的是 "<<“和”>>“优于”&“优于”^“优于”|"

上面是位运算优先级，逻辑运算优先级是 “非┐” > “和∧” > “或∨” > “蕴含→” > "双向蕴含←→"

贴个代码，方便理解：

#include
#include
#include
using namespace std;


//运算符优先级
int main()
{
    //"!" "~" 优先于 加减乘除 优先于 "<<" ">>" 优先于 ">" "<" ">=" "<=" 优先于 "==" "!="
    //优先于 "^" 优先于 "&" 优先于 "|" 优先于 "&&" 优先于 "||" 优先于 "?:" 优先于 "赋值"
    
    //验证
    //"~" > "<<"
    int a = ~1>>1;
    cout << a << endl;
    a = 1<<~0xffffffff;
    cout << a << endl;
    //"<<" 和 ">>" 同级
    a = 1<<2>>1;
    cout << a << endl;
    a = 8>>1<<1;
    cout << a << endl;
    //"<<" > "&"
    a = 8&4<<1;
    cout << a << endl;
    //"&" > "^"
    a = 2&3^3;
    cout << a << endl;
    //"^" > "|"
    a = 1&3|2&6;
    cout << a << endl;
    return 0;
}

1. 23 | 2 ^ 5 = 23而不是18。
2. 写位运算的时候要写括号(1 << i) <= dpt[y] - dpt[x]
3. 二分mid不用写括号:int mid = l + r >> 1

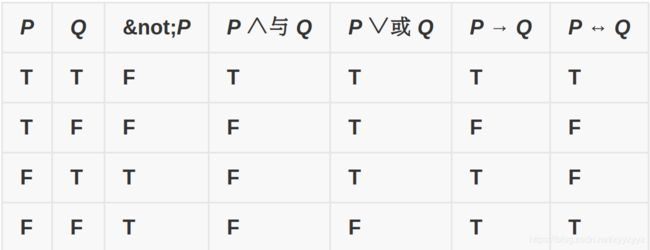
逻辑运算符

有几种看起来并不常见的运算符：

1. ¬取反
2. ∧与
3. ∨或
4. →条件
5. ↔双条件

真值表：

重点：

P→Q条件

举个例子：一个姓胡的人说：“如果太阳从西边升起，我就不姓胡。”这句话是对的，因为太阳不会从西边升起，P=False，所以不论Q是否正确，这句话都是正确的。而这里的“如果”并不表示假设，而是表示判断。

双条件

即等价命题。

e.g.

看到了就算一算。

12、若A=False，B=True，C=True，D=False，则下列逻辑运算真的有（）
A、(A∧B)V(C∧D) B、((A∧¬B)VD)∧B
C、((¬A→¬B)∧C)VD D、¬A∧(¬D→¬C)→¬B

ans=D

解析：D.假作为条件得到一定是真。

P、NP、NP-hard和NPC

巨佬博客：styx

定义

1. P：Polynomial problem，存在多项式复杂度算法的问题。
2. NP：Non-Deterministic Polynomial Problems（不能决定的P问题），一个问题的一个解可以用多项式级复杂度检验，它就是NP问题
3. NP-hard：可以使所有NP问题在多项式复杂度内归约到它的问题
4. NPC：可以使所有NP问题在多项式复杂度内归约到它的NP问题

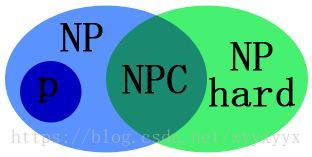
包含关系

注意事项

1. NP问题不是非P问题
2. P问题一定是NP问题（$P\in NP$）
3. NP-hard问题不全是NP问题
4. NP-hard问题不与NP问题相交的部分是无解问题（例如停机问题）
5. 如果解决了NPC问题就可以解决所有的NP问题，然后就可以证明P=NP

e.g.1

2012.20．以下关于计算复杂度的说法中，正确的有（ ）。
A．如果一个问题不存在多项式时间的算法，那它一定是NP类问题
B．如果一个问题不存在多项式时间的算法，那它一定不是P类问题
C．如果一个问题不存在多项式空间的算法，那它一定是NP类问题
D．如果一个问题不存在多项式空间的算法，那它一定不是P类问题

ans=BD

解析
A 还记得图灵停机问题吗？那是一个NP-hard而不是NP问题
B 这是对的，因为P问题的定义是存在多项式时间的复杂度算法
C、D 时间复杂度和空间复杂度都是复杂度，是等价的。

e.g.2

2013.14. （ ）属于 NP 类问题。
A. 存在一个 P 类问题
B. 任何一个 P 类问题
C. 任何一个不属于 P 类的问题
D. 任何一个在（输入规模的）指数时间内能够解决的问题

ans=AB

解析
这里考察的知识点是NP问题的定义以及P∈NP
由之前可知任何P问题都是NP问题，同理一定存在一个P问题是NP问题 AB都是对的 C的话我们可以继续用万能的停机问题去反驳他
D考察的是定义，指数时间内能解决不意味着多项式时间能验证解，所以D是错的

数论与数学

排列组合

e.g.

20、定义f(x):若x的二进制表示中有连续两个1，则f(x)=0,反之f(x)=1。定义g(x)=f(0)+f(1)+f(2)+…+f(x),则g(233)=___________。
A. 31 B. 43 C. 55 D. 76

ans=C

解析：
首先发现一下g(233)=g(255)，然后暴力枚举放几个1，排列组合算一下。
$ans=1+C_8^1+C_7^2+C_6^3+C_5^4=55$

e.g.

19.平面上有三条平行直线，每条直线上分别有7，5，6个点，且不同直线上三个点都不在同一条直线上。问用这些点为顶点，能组成多少个不同四边形？
A）1095 B）1620 C）2250 D） 4500

ans=C

解析：
就是在这些点里面选4个点，但是同一条直线最多只能选2个。
所以枚举选点个数：1) 2 + 2，2) 2 + 1 + 1。然后排列组合计算。

e.g.

3、给定4个变量x1,x2,x3,x4，满足1<=xi<=10,求方程x1+x2+x3+x4=30的解数（）。
A.282 B.288 C.360 D.362

ans=A

此题也可以DP做，在下面有写。千万不要容斥，不如DP。

解析：
设$y_i=10-x_i(i\in [1,4])$，那么$y_1+y_2+y_3+y_4=10,(y_i\in [0,9])$。
直接暴力算出没有上界限制的方案数$C_{13}^3=286$，然后减去某一项$y_i$为10的数量$4$，答案为$282$。

卡特兰数

1. 递推：$ca{t}_i={\sum }_{j=0}^{j\le i-1}ca{t}_j\ast ca{t}_{i-1-j}$，递推式用于从一个毫不相干的问题想到卡特兰数。
2. 组合数：$ca{t}_i=C_{2n}^n-C_{2n}^{n-1}=\frac{C_{2n}^n}{n+1}$，主要用于简便的计算。可以用斜线走网格的例子推出。

前几项为：1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, …

• 应用：来自这里

1. 一个足够大的栈的进栈序列为1,2,3,⋯,n时有多少个不同的出栈序列？

枚举最后一个出栈的数字$k$。那么$k$从入栈起就必须压在栈底直到最后弹出。所以在他前面进栈的必须在他进栈之前弹空，方案数$ca{t}_{k-1}$。在他后面进栈的必须在最后他弹出之前弹空，方案数$ca{t}_{n-k}$。在$k$之前和之后的互不影响。

所以得到递推式$ca{t}_i={\sum }_{j=0}^{j\le i-1}ca{t}_j\ast ca{t}_{i-1-j}$，就是卡特兰数。

变种：n个人拿5元、n个人拿10元买物品，物品5元，老板没零钱。问有几种排队方式。

2. 二叉树构成问题。有n个结点，问总共能构成几种不同的二叉树。

枚举根的左儿子右儿子数量递推，发现就是卡特兰数递推式。

3. 凸多边形的三角形划分。一个凸的n边形，用直线连接他的两个顶点使之分成多个三角形，每条直线不能相交，问一共有多少种划分方案。

选一个基准点，连出一条边，可以把$n$边形分成两块，一块大小为$i(3\le i\le n-1)$，另一块$n-i+2$

发现是卡特兰数递推式。

变式：在圆上选择2n个点,将这些点成对连接起来使得所得到的n条线段不相交的方法数？

4. 在n*n的格子中，只在下三角行走，每次横或竖走一格，有多少中走法？

其实向右走相当于进栈，向左走相当于出栈，本质就是n个数出栈次序的问题，所以答案就是卡特兰数。

5. n个长方形填充一个高度为n的阶梯状图形的方法个数？

把包含左上角的矩形去掉分出两块小阶梯，发现就是卡特兰数递推式。

斯特林数

第一类斯特林数

1. 公式：$dp[i][j]=dp[i-1][j-1]+dp[i-1][j]\ast (i-1)$
2. 意义：i个互不相同的元素，排成j个圆的方案数。
3. 理解：可以单独开一个圆，或放在之前某个元素的左边（规定左边之后就不会重复了）
4. 例题：hdu3625圆排

第二类斯特林数

1. 公式：$dp[i][j]=dp[i-1][j-1]+dp[i-1][j]\ast j$
2. 意义：i个互不相同的元素，放入j个相同的集合。
3. 理解：可以单独开一个集合，或放入之前某一个集合。

第二维比较小的时候可以矩阵快速幂优化（雾）。

主定理

若递推时间复杂度

$$T(n)=aT(n/b)+O(n^d)$$

那么

$$T(n)=\{\begin{array}{rlr}& O(n^{lo{g}_{b}a})& ,d<lo{g}_{b}a\\ & \Theta (n^{d}lgn)& ,d=lo{g}_{b}a\\ & \Omega (n^d)& ,d>lo{g}_{b}a\end{array}$$

首先，背下来。

其次，努力理解。

对于第二种情况，很容易就推出来了，$O(n^{lo{g}_{b}a}lo{g}_{b}n)$。
第一种和第三种情况以现在的水平还无法推导，只能感性理解。
第一种情况，f(n)的复杂度比较小，底数小于0，指数大起来之后求和趋近于1，于是$O(n^{lo{g}_{b}a})$。
第三种情况，f(n)复杂度大，底数大于0，复杂度趋向于f(n)，$O(f(n))$

等以后能理解了再写博客，三天之后要是用到了就背结论。

upd.根据Tiandong123的概括和升华，主定理就是谁大听谁的。

e.g.

简单应用

4、若某算法的计算时间表示为递推关系式：
T(N) = 2T(N / 4) + N^(1/2)
T(1) = 1
则该算法的时间复杂度为（ ）。
A. O(N^(1/2)) B. O(N log N) C. O(N^(1/2)logN) D. O(N^2)

ans=C

解析:$a=2,b=4,d=\frac{1}{2},lo{g}_{b}a=d,\therefore T(n)=\Theta (n^{d}lgn)=\Theta (\sqrt{n}lo{g}_{2}n)$

n个球放在m个盒子里

详见XJOI各种放球题目。

最难理解的是球同盒同的情况（可空或非空差不多）。相当于整数拆分。
递推方程：$f[i][j]=f[i-j][j]+f[i][j-1]$，边界$f[0][j]=1(j\ge 0)$。
意义是把所有盒子按照球的个数降序排序（以去重），可以YY每一种方案都可以被给一些前缀放球构造出来，所以对于$f[i][j]$可以选择给前$j$个盒子全都放一个球，或者新开一个盒子。
其实这个方程可以看成前缀和，把前缀和优化掉的那一维展开之后，
方程：$f[i][j]={\sum }_{k=1}^{k\le j}f[i-j][k]$，解释起来很难啊，可以把这个方程想成交换了x轴和y轴，给每一层（这个层就是原来方程的某一次放球）放球，最多放了前$j$个盒子。

这个$f[i][j]=f[i-j][j]+f[i][j-1]$呢，还可以看成用不大于$j$的整数组成$i$的方案数，自行YY。

再记一下球不同盒同非空的情况。
方程：$f[i][j]=f[i-1][j]\ast j+f[i-1][j-1]$，$f[i][j]$表示前$i$个球，放在$j$个盒子里的方案数。意义是对于当前的球，可以单独开一个新格子，或者放在已经有球的任意一个盒子里。因为盒子是相同的，可以YY成不同的盒子按照盒子里标号最小的那个球的序号升序排序。

三门问题

问题如下：

假设你正在参加一个游戏节目，你被要求在三扇门中选择一扇：其中一扇后面有一辆车；其余两扇后面则是山羊。你选择了一道门，假设是一号门，然后知道门后面有什么的主持人，开启了另一扇后面有山羊的门，假设是三号门。他然后问你：“你想选择二号门吗？你决定根据打开一号门三号门获得汽车的概率做出选择，那么选择三号门获得汽车的概率是（）。
A.1/6
B. 1/3
C. 1/2
D. 2/3

感觉好像是$\frac{1}{2}$，开门之后一号和三号门开出车的概率应该一样才对。

然而事实并非如此。

讨论一下，分两种情况：

1. 一开始我们选的门后面是车的概率是$\frac{1}{3}$，此时另外两个门都是羊，换门获得车的概率时$0$。
2. 同理，一开始我们选的门后面是羊的概率是$\frac{2}{3}$，此时另外两个门只有一个是羊，主持人必须要选这个有羊的门打开，那么剩下的那个门一定是车，换门拿车的概率是$1$。

所以换门拿车的总概率是$\frac{1}{3}\ast 0+\frac{2}{3}\ast 1=\frac{2}{3}$。

Lucas定理

csdn博客
洛谷博客
这两篇讲的不错，还是人能看得懂的。

结论记一记：$C_n^m={\prod }_{i=0}^{i\le lo{g}_p^n}{C}_{n[i]}^{m[i]}$，其中m[i]和n[i]是m和n在p进制下每一位的数字。

星期问题

公元元年1月1日是星期一，明明一点用都没有。

公式不用像网上那样，化着化着失去了他本来的样子，按照日期安排的规律去推也很快。

dd[12] = {0, 3, 3, 6, 1, 4, 6, 2, 5, 0, 3, 5};
cin >> y >> m >> d;
ans = ((y-1)+(y-1)/4-(y-1)/100+(y-1)/400
	   +dd[m-1]
	   +d
	   +(((y%4 == 0 && y%100 != 0) || (y%100 == 0 && y%400 == 0)) && m >= 2))%7;

比如2018年10月13日初赛是星期六，1926年8月17日somebody的生日是星期二 蛤蛤蛤

进制转换

简称

1. B - Binary - 二进制

2. O - Octet - 八进制

3. D - Decimal - 十进制

4. H - Hex - 十六进制

幻方

奇数阶

斜着走，到边界跳回第一个，被填掉了就去上方。

4	9	2
3	5	7
8	1	6

偶数阶

百度百科

分两种情况讨论。

四阶

DP

计数DP

数数题最好玩了。

e.g.

3、给定4个变量x1,x2,x3,x4，满足1<=xi<=10,求方程x1+x2+x3+x4=30的解数（）。
A.282 B.288 C.360 D.362

ans=A

$dp[i][j]$表示前i个变量，和为j的方案数。

先写出递推式$dp[i][j]=dp[i-1][j-k](k\in [1,10],j-k\ge 0)$

边界$dp[0][0]=1$

列表爆算开始：

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
1	1	1	1	1	1	1	1	1	1	1	0	0	0	0	0	0	0	0	0	0
2	0	1	2	3	4	5	6	7	8	9	10	9	8	7	6	5	4	3	2	1	0	0	0	0	0	0	0	0	0	0
3																				63	55	45	36	28	21	15	10	6	3	1
4																														282

没有写的都是不需要算的。其实计算量不大。

此题也可以容斥来做。此题也可以直接组合数做。

概率期望DP

初赛的概率期望DP一般不会太难，但是要尽量减少算法复杂度，比如用作差，方程移项

状态最好按照倒推的思路去设计，因为需要一个走到就停止的终止状态作为递推的初始值。如果正推，最好把状态设计成从起点第一次到达某个位置的期望。

例题一道：
一只青蛙，从5开始跳，每次等概率跳到自己或者比自己编号小的位置，跳到1的时候停止，求从5跳到1的期望步数。

状态：$f[i]$表示从i跳到0的期望。
初始状态：$f[1]=0$
转移方程：$f[i]=\frac{{\sum }_{j=1}^{j\le i}f[j]}{i}+1$（这里j<=i）
移项：$f[i]=\frac{{\sum }_{j=0}^{j<i}f[j]}{i-1}+\frac{i}{i-1}$（这里j 所以：$f[1]=0,f[2]=2,f[3]=5/2,f[4]=17/6,f[5]=37/12$，答案为37/12

超基础图论

欧拉各种路的区分

1. 欧拉路：如果图G中的一个路径包括每个边恰好一次，则该路径称为欧拉路径。
2. 欧拉回路：如果一个回路是欧拉路径，则称为欧拉回路。
3. 欧拉图：有欧拉回路的图
4. 半欧拉图：有欧拉路径但没有欧拉回路的图
5. 欧拉迹：同1
6. 欧拉闭迹：同2

tips： 欧拉图不一定要联通，可以有度为0的点被孤立，因为只要求经过每条边。但满足没有奇数度的定点的图不一定是欧拉图，因为可以分成多个不联通的欧拉图。

哈密尔顿通路/回路

毕竟是初赛，记几个结论就好了。。。

1.设G具有n个结点的简单图，如果G中每一对结点度数之和大于等于n-1，则在G中存在一条汉密尔顿路。

最小染色数

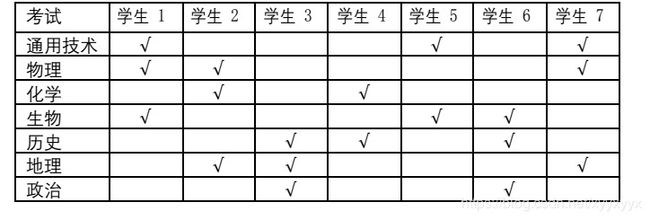
e.g.

2. 某中学在安排期末考试时发现，有 7 个学生要参加 7 门课程的考试，下表列 出了哪些学生参加哪些考试（用√表示要参加相应的考试）。 最少要安排_________个不同的考试时间段才能避免冲突？

ans=3

把不能在同一时间考的科目连边，连边的两点不能同色，求最小染色数。

阅读程序写结果

模拟

#include    
using namespace std;  
int a,b,c,d,e;
int main() {
	a=1;b=a+2;c=b+3;d=c+4;a=d+5;
	for(int e=1;e<=4;e++){
		if(a%2==0) a=a/2+d;
		else a=a/2+d+1;
		b=a+2;c=b+3;d=c+4;a=d+5;
	}	
	cout<<a<<endl;
    return 0;
}

ans=152

#include   
using namespace std;  
int x, y;  
long long tot;  
int f(int x, int y) {  
tot++;  
    int ans = y;  
    for (int i = 1; i <= y - x; ++i)  
        ans += x / i * f(x + i, y - i);  
    return ans;  
}  
int main() {  
    scanf("%d%d", &x, &y);  
printf("%d\n", f(x, y));  
}  

3、若输入：2 10，则输出为（）。
A． 278 B．713 C．1112 D．1653
4、程序结束，tot的值为29，请判断结果是否正确（）。
A、正确 B、错误

ans=D；B

列表手膜：

首先是答案：

(x,y)	ans
(10,2)	2
(9,3)	3
(8,4)	4
(7,5)	5
(6,6)	6
(5,7)	7 + 5 * 6 + 2 * 5 = 47
(4,8)	8 + 4 * 47 + 2 * 6 + 1 * 5 + 1 * 4 = 217
(3,9)	9 + 3 * 217 + 1 * 47 + 1 * 6 = 713
(2,10)	10 + 2 * 713 + 1 * 217 = 1653

然后是tot：

(x,y)	tot
(10,2)	1
(9,3)	1
(8,4)	1
(7,5)	1
(6,6)	1
(5,7)	1 + 1 + 1 = 3
(4,8)	1 + 3 + 1 + 1 + 1 = 7
(3,9)	1 + 7 + 3 + 1 + 1 + 1 + 1 = 15
(2,10)	1 + 15 + 7 + 3 + 1 + 1 + 1 + 1 + 1 = 31

看出程序目的

#include   
using namespace std;
int a[10000];
int gcd(int m,int n){
 while(n){
 	int r=m%n;m=n;n=r;
 }
 return m;
}
int main(){
 int n=1000,r=202;
 for(int i=1;i<=n-r;i++) a[i]=n-i+1;
 for(int i=2;i<=r;i++){
 	int k=i;
 	for(int j=1;j<=n-r;j++)
 	if(gcd(k,a[j])>1){
 		int g=gcd(k,a[j]);
 		k/=g; a[j]/=g;
 		if(k==1) break;
	 }
 }
int p=1,g=0;
 for(int i=1;i<=n-r;i++){
 	p*=a[i];
 	while(p%5==0){
 		p/=5; g++;
	 }
	 p%=5;
 }
 cout<<g<<endl;
 return 0;
}

ans=151

解析：
ans=203到1000中因数5的个数-1到202中因数的个数
=1到1000中因数5的个数-2*(1到202中因数的个数)

#include  
using namespace std;  
int n,ans=0;  
int dfs(int row,int ld,int rd) {  
	int lim=(1<<n)-1;  
	int p,pos;  
	if(row!=lim) {  
		pos=lim&~(row|ld|rd);  
		while(pos) {  
			p=pos&-pos;  
			pos^=p;  
			dfs(row|p,(ld+p)<<1,(rd+p)>>1);  
		}  
	} else ans++;  
}  
int main() {  
	cin>>n;  
	dfs(0,0,0);  
	cout<<ans;  
}  

9、输入为8，结果为（）？
A. 40 B. 67 C. 92 D. 108

假题，看看就好了。

ans=C

解析很难看出这是一个八皇后。。。就算你看出来了，也数不出来。反正也就6分，蒙一个，期望得分1.5分。

完善程序

具体算法

1、 现在政府计划在某个区域的城市之间建立高速公路，以使得其中任意两个城市之间都有直接或间接的高速公路相连。费用为每千米一个单位价格，求最小费用。
输入：n（n<=100，表示城市数目）
接下来n行每行两个数xi，yi，表示第i个城市的坐标。（单位：千米）
输出：最小费用（保留两位小数）

#include   
#include    
#include   
using namespace std;    
const int MaxN=101;  
struct Tcity{  
	double x,y;  
}c[MaxN];  
double d[MaxN][MaxN];  
int p[MaxN];  
inline double pingfang(double a){return (1);}
int main() {  
	int n;  
	cin>>n;  
	for(int i=1;i<=n;i++) cin>>c[i].x>>c[i].y;  
	for(int i=1;i<=n;i++)  
		for(int j=1;j<=n;j++)  
		d[i][j]=sqrt(pingfang(c[i].x-c[j].x)+pingfang(  (2)  ));
	p[1]=0;  
	for(int i=2;i<=n;i++) (3);
	double ans=0;  
	for(int i=1;i<n;i++){  
		double Min=1e10;  
		int k;  
		for(int j=1;j<=10;j++)  
			if(  (4)  ){Min=d[p[j]][j];  (5) ;}  
		ans+=d[p[k]][k];  
		p[k]=0;  
		for(int j=1;j<=n;j++) if(  (6)  )p[j]=k;
	}  
	cout<<fixed<<setprecision(2)<<ans<<endl;  
    return 0;  
}  

ans:
a*a
c[i].y-c[j].y
p[i]=1
p[j]>0&&d[p[j]][j] k=j
d[k][j]

毒瘤题

< AGC >
Ringo Mart是一家便利店，出售苹果汁。
在Ringo Mart开业当天，早上有A罐罐装果汁。Snuke每天在白天购买B罐果汁。 然后，Ringo Mart的经理每晚检查剩余库存的果汁罐数。如果有C或更少的罐头，D新罐将在第二天早上添加到库存中。
确定Snuke是否可以无限期购买果汁，也就是说，当他试图购买果汁时，总会有B罐或更多罐装果汁。除了Snuke之外，没有人在这家商店买果汁。
请注意，此问题中的每个测试用例都包含T个查询。
输入格式
第一行T，接下来T行每行A，B，C，D。
输出：对每个询问，若可以，输出“Yes”，否则输出“No”。

#include 
using namespace std;
#define ll long long 
int T; ll a, b, c, d;
int main(){
  for ( cin >> T ;  T--; ){
    cin >> a >> b >> c >> d;
    if (  （1）  || （2）){
      puts("No");
      continue;
    }
    a  （3）  b;
    a  （4）  d;
    ll g = __gcd(b , d);
    puts( （5） / g < (b – 1 – a + d) / g? "No": "Yes");
  }
}

1、A. c>d	B. a<b
2、A. c<a	B. d < b	C. a<c 		D. c<b
3、A. *=	B. %=		C. /= 		D. -=
4、A. *=	B. %=		C. /= 		D. -=
5、A. (c+b-d)	 	B. (c-b+d)		C. (c-a+d) 		D. (c+b-a)

ans:
BBDBC

问题描述：
对于任意给出的一个正整数n(n<=50000)，求出具有n个不同因子的最小正整数m。（例如：但n=4时m=6，因为6有4个不同整数因子：1、2、3、6，并且是最小的有4个因子的整数。）
程序：

#include  
#include  
#include  
#include  
using namespace std;  
#define maxn 50000  
long p[17]= {0,2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53};  
long f[501],c[501],minc[501],m[20000];  
long h,i,j,k,l,n,t,total;  
float mins,s;  
void resolve(long dep,long m,long r) {  
	long i;  
	if (r==1) {  
		s=0;  
		for (i=1; i<=dep-1; i++) s=s+     ①     ;  
		if (s < mins) {  
			mins=s;  
			l=dep-1;  
			for (i=0; i<=500; i++) minc[i]=c[i];  
		}  
	} else {  
		for (i=m; i<=total; i++)  
			if (     ②     ) {  
				c[dep]=f[i];  
				resolve(dep+1,     ③     );  
			}  
	}  
}  
void mul(long t) {  
	for(k=0; k<=h; k++) m[k]=m[k]*t;  
	for(k=0; k<=h; k++) {  
		m[k+1]=m[k+1]+m[k]/10;  
		m[k]=m[k] % 10;  
	}  
	while (     ④     ) {  
		m[h+2]=m[h+1] / 10;  
		m[h+1]=m[h+1] % 10;  
		++h;  
	}  
}  
int main() {  
	scanf("%ld",&n);  
	total=0;  
	for (i=n; i>=2; i--)  
		if (n % i == 0) {  
			++total;  
			f[total]=i;  
		}  
	mins=LONG_MAX;  
	resolve(1,1,n);  
	for (i=1; i<=15000; i++) m[i]=0;  
	m[0]=1;  
	h=0;  
	t=1;  
	for (i=1; i<=l; i++)  
		for (j=1; j<=minc[i]-1; j++)  
			if (p[i]<2000000000 / t)  
				t=t*p[i];  
			else {  
				mul(t);  
				⑤     ;  
			}  
	mul(t);  
	for (i=h; i>=0; i--) printf("%ld",m[i]);  
	printf("\n");  
	return 0;  
}  
1、A. c[i]*log(p[i])	B. (c[i]-1)*log(p[i])	C. c[i]*p[i]		D. c[i]*log(p[i]+1)  
2、A. f[i]%r==0		B. f[i]%r!=0		C. r%f[i]==0		D. r%f[i]!=0  
3、A. i,r%c[dep]	B. i+1,r/c[dep]		C. i+1,r%f[i]		D. i,r/f[i]  
4、A. m[h+2]>0		B. m[h+1]>0		C. m[h]		        D. k<total  
5、A. m[i]=p[i]		B. m[i]=t*p[i]		C. t=p[i]		D. t=t*p[i]  

ans:
B; C; D; B; C

题意很简单。

因为$m=\sum p_i^{x_i}$的因数个数为$n=\prod (x_i+1)$，所以爆搜$n=\prod c_i$的拆分。

要使最终数尽量小，就把较大的$c_i$分给较小的$p_i$，得到$m=\prod p_i^{c_i-1}$。

因为爆long long无疑，所以比较大小的时候改用log，即比较$\log m=\sum (c_i-1)\ast \log p_i$。

最后求答案，不一次一次的高精乘，而是把乘的数存在$t$里，在$t$快要爆的时候高精乘。

注意检查。

总结

• 选择题：

能拿的分尽量拿，没听说过的计算机基础知识排除完了尽量蒙。

不要看着B选C。。。

答案不要抄错。。。

• 数学题：

草稿一定要打清楚，划出专门的一块来做一道题。假如可以直接排列组合就不要DP，假如可以DP就不要手膜记忆化搜索树。

写DP表格画大画清楚。

多算几遍。。。而且CSP搞成选择题了，除非方法错，应该对不上选项就知道错了。

• 看程序写输出：

手膜题至少膜2遍。能看出程序在干什么最好，但是最好留下最后的时间略微手膜。

注意细节。比如某年的结尾逗号，某年堆排数组下标：ch[20]={‘q’,‘S’,‘O’,‘R’,‘T’…}，那个’q’要了就死了。

• 程序填空：

尽量先看懂算法。想必CCF也不会搞出什么高端的东西。然后选择题对细节要求降低，实在不行联系上下文就好了。

今天2019.10.17，后天初赛。希望利用好明天一天，后天利用好早上两个小时，稳定发挥。

加油。

upd.

今天2019.10.18，明天就是初赛了。经过前面几个星期的系统复习，我觉得稳过初赛一点问题都没有。现在需要做的就是调整好状态，明天考试保持清醒和谨慎，把控好时间，留足时间检查。不要犯低级错误。

加油！

go to top