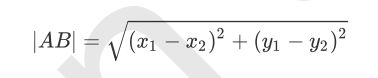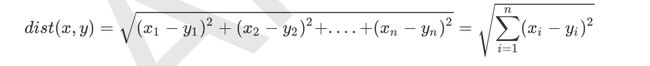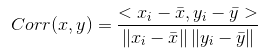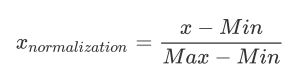机器学习KNN算法基本原理与python实现
机器学习KNN算法基本原理与python实现
k-近邻算法(k-Nearest Neighbour algorithm),又称为KNN算法,是数据挖掘技术中原理最简单的算法。KNN
的工作原理:给定一个已知标签类别的训练数据集,输入没有标签的新数据后,在训练数据集中找到与新数据最邻
近的k个实例,如果这k个实例的多数属于某个类别,那么新数据就属于这个类别。可以简单理解为:由那些离X最
近的k个点来投票决定X归为哪一类
简单来说，一个待分类的样本数据，在使用knn算法的时候，根据自己训练样本的数据特征，选取k的值至关重要，当然K的取值是人为定义好的，通常不超过20. 举个例子，如果有6个训练数据，分别是A,A,A,B,B,B，有一个待测样本数据C，根据KNN算法，需要预测数据C进行归类，如果选取的K=1,那么离待测样本数据最近的一个点的归类，比如是B，那么待测样本数据C就归属于B类，同理，如果选取的K=5,那么离C最近的5个点，有A,A,A,B,B,那么C就数据A类，
KNN的距离计算公式
上面也提到过，KNN算法，选取k的值不同，离待测样本数据距离最近点的不同，得到的结果也就不同.因此距离的计算尤其重要，在二维平面中，距离的计算公式为，
当有多个特征拓展到N维的空间当中，我们可以使用欧几里得度量(欧氏距离）来得到他们之间的距离，距离计算公式如下:
其中 
表示待测样本的特征值，
表示训练样本的特征值
举个例子 a（x1,x2,x3）,b (y1,y2,y3)
那么他们之间的欧式距离是
皮尔逊相关系数
在欧式距离的计算中，不同特征之间的量级对欧式距离的影响比较大，例如A=(0.05,1),B=（1,1）,C=（0.05,4），我们就不能很好的判断出A和B，A和C 之间的距离，而皮尔逊相似性的度量对量级则可以，其公式如下:
其中
当然了，在KNN 算法在计算距离的时候,不仅仅只有欧式距离来进行计算，还有各种其他距离公式比如明可夫斯基距离、曼哈顿距离、切比雪夫距离等等，由于本人时间有限，对此就不一一作出详细的介绍了，想了解的话，可以自行去问度娘
KNN算法实现步骤如下
(1)计算已知类别数据集中的点与当前点之间的距离;
(2)按照距离递增次排序；
(3)选取与当前点距离最小的k个点
(4)确定前k个点所在类别的出现频率
(5)返回前k个点出现频率最高的类别作为当前点的预测类别
KNN算法的Python实现
本人使用的编译器jupyter notbook
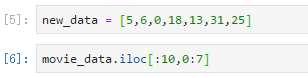
第一步 ：构建数据集，为了方便验证，这里使用python字典dict构建数据集，并将其转化为DataFrame形式
第二步:计算已知类别数据集中的点与当前点之间的距离
第三步:将距离升序排列，然后选取距离最小的K个点
第四步:确定前K个点所在类别出现的频率
第五步:选取频率最高的类别作为当前点的预测类别
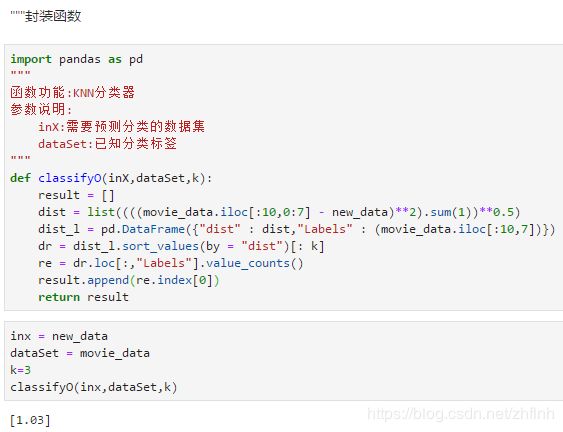
封装函数
完整的流程已经实现，需要把函数进行封装，方便后期的调用
上述就是我们使用k近邻算法构建的分类器，但是分类器的给出的结果并不是百分百正确，我们也可以通过很多方法来验证分类器给出的结果是否是正确的，分类器结果的性能也会受到很多因素的影响，比如k的取值很大程度上影响分类器的结果，还有分类器的设置，原始数据集等等一系列因素，我们把原始数据分为训练集和测试集，上述代码发现一个问题，k近邻算法没有进行数据的训练，直接使用未知的数据和已知数据进行比较，得到结果，所以说。k近邻算法没有显示的学习过程
数据归一化
数据归一化的优点 :
1 提高梯度下降法求解最优解的速度 2 归一化之后也可能提高精确度
在KNN算法中，如果一个特征值域范围非常大，那么距离计算就主要取决于这个特征，从而与实际情况相悖（比如这时实际情况是值域范围小的特征更重要）
数据归一化的方式有很多，比如0-1标准化、Z-score标准化、Sigmoid压缩法等等，下面介绍下0-1标准化的处理公式:
x:表示当面需要归一化的数值
Min:表示这个特征下的最小值
Max:表示这个特征下的最大值