数据结构课程设计（三）---Huffman编码

1、任务简述：
对一篇英文文章，统计其中26个小写字母出现的频次，对这些小写字母进行Huffman编码。

要求：
（1）从文件读入原始文本文件，并在屏幕上显示出文本；
（2）按照字母顺序输出字母的出现次数，以及相应的编码。
（3）同时具备解码功能。即输入一串二进制编码，能够还原出文本
2、算法描述：
数据结构:

一颗有n个叶子（n个字符得文章）结点的Huffman树共有2n-1个结点，可以存储在一个大小为2n-1的一维数组中。译码需要从上往下走，编码需要从下往上走，所以对于每个节点都需要知道其双亲，同时也要知道其孩子的信息，所以定义如下结构：

准备操作：
1.寻找文章中不同字符的个数，并且保存到数组c中，这个只需要对文章进行一次遍历即可。
2.寻找数组c中没有双亲的节点中最小的两个值，由于在写这题的时候，我还没有学习到那些厉害的排序方法，而且感觉经典的排序算法有些繁琐，所有我查阅了相关资料，采用打擂法。
3.把Huffman编码以位存储进文件：这里我不是很会，请教了高中的同学，具体方法见总结。

编码，解码：
由于赫夫曼树中没有度为1的结点(这类树又称严格的(strict)(或正则的)二叉树),则一棵有n个叶子结点的赫夫曼树共有2n-1个结点,可以存储在一个大小为2n-1的一维数组中。如何选定结点结构?由于在构成赫夫曼树之后,为求编码需从叶子结点出发走一条从叶子到根的路径;而为译码需从根出发走一条从根到叶子的路径。则对每个结点而言，既需知双亲的信息,又需知孩子结点的信息。
把所有出现的字符（n个）权值先录入表，双亲、左孩子、右孩子均置为0。
编码：然后从n—2n-1的空间，依次选取表中权值最小的两个结点，保持最小左边，次小右边（确定唯一编码），结成新的结点存入表中，更新双亲、左右孩子信息。
解码时从2n-1开始寻找，1右孩子、0左孩子、一直寻找到一个左右孩子均为0的结点，就是那个字符。

3、源代码

#include 
#include 
#include  
#include 
#include 
using namespace std;

typedef struct
{
	int weight;
	int parent, lchild, rchild;
}HTNode, * HuffmanTree;

typedef char** HuffmanCode;		//用于储存赫夫曼编码结果

int FindNextNoParent(HuffmanTree HT, int x, int cur)//寻找表中没有双亲的节点
//cur是起始点、x为查找末端
{
	int i;
	HuffmanTree p = HT;
	for (i = cur; i <= x; i++)
	{
		if ((p + i)->parent == 0)
		{
			return i;
		}
	}
	return -1;
}

void Select(HuffmanTree HT, int x, int& s1, int& s2)//选择已经建成的表中两个最小的、且没有双亲的节点，赋给s1、s2
//x为最后一个查找末端
{
	int cur;
	s1 = FindNextNoParent(HT, x, 1);
	cur = s2 = FindNextNoParent(HT, x, s1 + 1);
	int i;
	int tmp;
	HuffmanTree p = HT;
	if (p[s1].weight > p[s2].weight)
		//保持最小的左边（s1），次小的右边（s2）
	{
		tmp = s2;
		s2 = s1;
		s1 = tmp;
	}

	while ((cur = FindNextNoParent(HT, x, cur + 1)) != -1)
		//打擂法，不断寻找表中权值最小的两个节点
	{
		if (p[cur].weight < p[s2].weight)
		{
			s2 = cur;
			if (p[s1].weight > p[s2].weight)
				//保持最小的左边（s1），次小的右边（s2）
			{
				tmp = s2;
				s2 = s1;
				s1 = tmp;
			}
		}
	}
}

void HuffmanCoding(HuffmanTree& HT, HuffmanCode& HC, int* w, int n)
//w是存储权值的编码，n是字符个数
{
	int m;
	int i;
	HuffmanTree p;
	int s1, s2;

	char* cd;
	int c, f;
	int start;

	if (n <= 1) return;
	m = 2 * n - 1;
	HT = new HTNode[m + 1];			//0号单元不使用
	for (p = HT + 1, i = 1; i <= n; i++, p++, w++)
		//先把所有的双亲结点、左孩子有孩子都置为零
		//顺便把权值输入表中
	{
		p->weight = *w;
		p->parent = p->lchild = p->rchild = 0;
	}
	for (; i <= m; i++, p++)
	{
		p->weight = p->parent = p->lchild = p->rchild = 0;
	}

	for (i = n + 1; i <= m; i++)
	{
		Select(HT, i - 1, s1, s2);//选择最小的两个无双亲节点
		HT[s1].parent = i; HT[s2].parent = i;
		HT[i].lchild = s1; HT[i].rchild = s2;
		HT[i].weight = HT[s1].weight + HT[s2].weight;
	}

	HC = new char* [n + 1];
	cd = new char[n];
	cd[n - 1] = '\0';
	for (i = 1; i <= n; i++)
	{
		start = n - 1;
		for (c = i, f = HT[i].parent; f != 0; c = f, f = HT[f].parent)//进行编码
		{
			if (HT[f].lchild == c)
			{
				cd[--start] = '0';
			}
			else
			{
				cd[--start] = '1';
			}
		}
		HC[i] = new char[n - start];
		strcpy(HC[i], &cd[start]);
	}
	delete[]cd;
}

int GetNum(int*& n, char*& c)		//读取文件字符种类和数量
//n用于存储不同字符对应的个数，c用于存储字符,返回字符的种类数量
{
	char ch;
	int count = 0;
	int flag;
	fstream rf;
	rf.open("source.txt", ios::in);
	if (rf.fail())
	{
		cout << "打开resource.txt文件失败" << endl;
		exit(0);
	}

	n = new int[100];
	c = new char[100];
	for (int i = 0; i < 100; i++)
	{
		n[i] = 0;
		c[i] = '\0';
	}
	while (!rf.eof())
	{
		rf.get(ch);
		flag = 0;
		for (int i = 0; i < count; i++)//查找该字符是否已存在
		{
			if (c[i] == ch)//如果已存在数量+1
			{
				n[i]++;
				flag = 1;
				break;
			}
		}
		if (flag == 0)//说明并未找到该字符 为新字符;
		{
			c[count] = ch;
			n[count]++;
			count++;
		}
	}

	rf.close();
	return count;
}

int HuffmanInFile(HuffmanCode HC, char* c, int count)
//把Huffman编码以位存储进文件，因为只能8位8位输入，所以返回最后多余的位数。
//HC是编码二维数组，count是字符种类
{
	int i, j;
	int times = 0;
	char ch;
	char CH = 0;
	fstream wf, rf;
	rf.open("source.txt", ios::in);
	if (rf.fail())
	{
		cout << "sourse.txt打开失败" << endl;
		exit(0);
	}

	wf.open("code.dat", ios::out | ios::binary);
	if (wf.fail())
	{
		cout << "code.dat打开失败" << endl;
		exit(0);
	}

	while (1)
	{
		rf.get(ch);
		if (rf.eof())
		{
			break;
		}
		for (i = 0; i < count; i++)
		{
			if (c[i] == ch)
			{
				i++;
				break;
			}
		}
		for (j = 0; HC[i][j] != '\0'; j++)
		{
			if (HC[i][j] == '0')
			{
				CH |= 0 << 7 - times++;
			}
			else
			{
				CH |= 1 << 7 - times++;
			}
			if (times == 8)
			{
				wf.write((char*)&CH, sizeof(char));
				CH = 0;
				times = 0;
			}
		}
	}
	wf.write((char*)&CH, sizeof(char));
	wf.close();

	return 8 - times;
}

void HuffmanOutFile(HuffmanTree HT, char* c, int count,int noneed)//把用Huffman编码好的code.dat文件译码存入resource.txt文件中
//HT为Huffman树，c是种类数组，count是字符种类数，noneed是多余位数
{
	fstream wf, rf;
	rf.open("code.dat", ios::in | ios::binary);

	if (rf.fail())
	{
		cout << "code.dat打开失败" << endl;
		exit(0);
	}

	wf.open("resource.txt", ios::out);
	if (wf.fail())
	{
		cout << "resource.txt打开失败" << endl;
		exit(0);
	}
	char ch,tch;//由于eof的判断性质，所以用tch来提前存取下一个要读取的字符，这样可以保证ch是最后一个字符
	int i;
	int p, times = 0;
	rf.read((char*)&ch, sizeof(char));
	rf.read((char*)&tch, sizeof(char));

	while (1)
	{
		p = count * 2 - 1;
		while (1)
		{
			if ((ch & (1 << 7 - times)) != 0)//若第i+1位为1
			{
				if (HT[p].lchild != 0)
				{
					p = HT[p].rchild;
				}
				else
				{
					break;
				}
			}
			else//若第i+1位为0
			{
				if (HT[p].lchild != 0)
				{
					p = HT[p].lchild;
				}
				else
				{
					break;
				}
			}
			times++;
			if (times == 8)
			{
				ch = tch;
				rf.read((char*)&tch, sizeof(char));
				if (rf.eof())//说明ch就是最后一个
				{
					times = 0;
					while (8 - times > noneed)//后面的多余位数便不用再读取
					{
						if ((ch & (1 << 7 - times)) != 0)//若第i+1位为1
						{
							if (HT[p].lchild != 0)
							{
								p = HT[p].rchild;
							}
							else
							{
								break;
							}
						}
						else//若第i+1位为0
						{
							if (HT[p].lchild != 0)
							{
								p = HT[p].lchild;
							}
							else
							{
								break;
							}
						}
						times++;
					}
					cout << c[p - 1];
					wf.put(c[p - 1]);
					rf.close();
					wf.close();
					return;
				}
				times = 0;
			}
		}
		if (p <= count)
		{
			cout << c[p - 1];
			wf.put(c[p - 1]);
		}
	}
	/*	if ((j & (1 << 10)) != 0)
			printf("指定位上为1");
		else
			printf("指定位上为0");
			*/
}

int main()
{
	int i;
	int count;//字符种类数

	HuffmanTree HT;
	HuffmanCode HC;//从1开始

	fstream file;

	int* value;//权值
	char* c;//字符种类
	count = GetNum(value, c);//获取字符种类，并把字符存入数组c
	HuffmanCoding(HT, HC, value, count);//构造Huffman树

	file.open("Huffman.txt", ios::out);
	for (i = 1; i <= count; i++)//存入文件
	{
		file << setw(2) << c[i - 1] << "出现次数：" << setw(5) << value[i - 1] << "    编码：" << setw(15) << HC[i] << endl;
	}
	file.close();

	int noneed = HuffmanInFile(HC, c, count);//对文件进行编码然后存入code.date

	HuffmanOutFile(HT, c, count, noneed);//根据Huffman树解码文件并存入resource.txt中
}//357行

三、运行结果
下图为显示原始文本：

下图为按照字母顺序输出字母的出现次数，以及相应的编码：


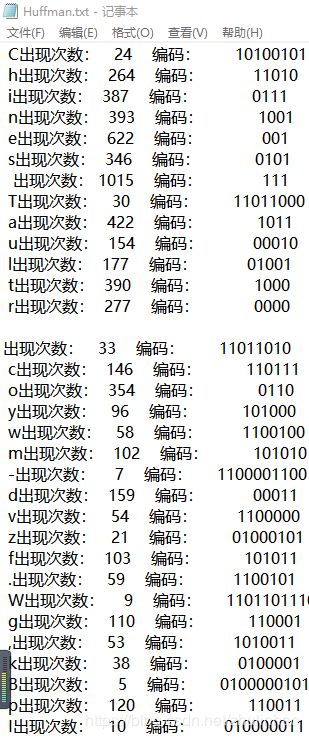
解码结果：


5、总结
性能分析：
时间复杂度：在建树的时候需要寻找两个最小的权值，所以时间复杂度为O(n^2)
空间复杂度：O(n)，n为文章中不字符的个数。
遇到的问题与解决方法：
难点在于位操作：
因为一次只能录入8位、所以在编码的时候不仅要循环考虑进行位操作的字符，还要考虑编码串的长度。（例如进行位操作的字符8位已经用完了，但是当前编码字符的01串还没有录到底）。而且编码到最后时，可能最后一个字符串只用了前几位、后面有几位是多余的。则需要返回这个多余位数、便于解码的最后进行判断。
心得体会：
运行结果正确，按照书上算法思路操作实现。本来打算只考虑26个英文字母，但是感觉可以多考虑一些，毕竟算法思路一样，所以考虑了我找的文章中出现的所有的字符，比如:“：”，“，”，“.”，“ ”，“ ”等等所有文中出现的字符。
存在问题和改进方法：
对于代码本身，问题应该不是很大，但是这题在生成编码的时候，我没有采用书上的思路，而是用了别人教给我的位操作，因为这部分内容，我可以写出来，但是感觉代码去判断左右孩子，来分配0，1较为麻烦，我想到是思路是：对每一个字符，为了确定其编码，我们可以对二叉树进行遍历，左孩子就是0，右孩子就是1，可以用数组来存储其编码。