Octave操作总结
目录
- 基本运算
- 逻辑运算
- 变量
- 函数
- 向量和矩阵
- 控制语句和函数
- 加载和保存数据
- 绘制图形
- 功能表
基本运算
+,-,*,/,^等运算
>> 3+3
ans = 6
>> 4^0.5
ans = 2
逻辑运算
常用的逻辑运算包括:等于(==)、不等于(~=)、并(&&)、或(||)四种,分别用不同的符号表示。
运算的结果用 1表示成立,0表示不成立。
>> 1 == 1
ans = 1
>> 1 ~= 1
ans = 0
>> 1 && 0
ans = 0
>> 1 || 0
ans = 1
变量
定义变量,语法跟其他语言也比较类似:
>> a = 3
a = 3
>> a = 3;
>> b = 'hi'; % 因为加了;号,没有打印出b的值
>> b % 直接输入变量名称,即可打印变量值
b = hi
>> c = (3 >= 1)
c = 1
>> a = pi;
>> a
a = 3.1416
注:字符串用 ‘’ 号 ,% 为注释符,在第一次执行a = 3的后面没有加 ; 号,Octave在执行完赋值语句后又打印出了变量a的值。而在第二句中,我们在赋值语句的末尾添加了 ; 号,这个时候,Octave只会执行赋值语句,将不再打印变量值。
函数
% disp函数打印变量值
>> a = pi;
>> disp(a)
3.1416
% 结合printf函数,实现格式化打印
>> disp(sprintf('2 decimals: %0.2f', a))
2 decimals: 3.14
>> disp(sprintf('6 decimals: %0.6f', a))
6 decimals: 3.141593
% 利用format long、format short也可以指定打印的精度,在Octave中,short是默认的精度
>> format long
>> a
a = 3.14159265358979
>> format short
>> a
a = 3.1416
注:在Octave中内置了很多的函数,有时,我们可能记不太清某个函数的具体用法,这个时候,Octave给我们提供了 help 命令,通过这个命令可以查看函数的定义以及示例。比如,我们想看下help这个函数怎么用,可以输入:help help。
向量和矩阵
在Octave中可以这样定义矩阵:将矩阵的元素按行依次排列,并用[]包裹,矩阵的每一行用;分割。
下面定义了一个3×2的矩阵A:
>> A = [1 2; 3 4; 5 6]
A =
1 2
3 4
5 6
注:; 号在这里的作用可以看做是换行符,也就是生成矩阵的下一行。
向量的创建:
>> V1 = [1 2 3]
V1 =
1 2 3
>> V2 = [1; 2; 3]
V2 =
1
2
3
注:V1是一个行向量,V2是一个列向量。
其他一些写法:
>> V = 1: 0.2: 2
V =
1.0000 1.2000 1.4000 1.6000 1.8000 2.0000
注:1 为起始值,0.2为每次递增值,2为结束值
>> v = 1:5
v =
1 2 3 4 5
注:1 为起始值,1为每次递增值,5为结束值
Octave内置的函数来生成矩阵,比较常用的几个函数是ones、zeros、rand、eye。
ones(m, n) 函数生成一个m行n列的矩阵,矩阵中每个元的值为1。
zeros(m, n) 函数生成一个m行n列的矩阵,矩阵中每个元的值为0。
rand(m, n) 函数生成一个m行n列的矩阵,矩阵的每个元是0到1之间的一个随机数。
eye(m) 函数生成一个大小为m的单位矩阵。
>> A = ones(3,3)
A =
1 1 1
1 1 1
1 1 1
>> B = zeros(3,3)
B =
0 0 0
0 0 0
0 0 0
>> B = rand(3,3)
B =
0.919518 0.028838 0.435431
0.696980 0.910511 0.378312
0.811546 0.171893 0.835920
>> B = eye(3)
B =
Diagonal Matrix
1 0 0
0 1 0
0 0 1
size函数返回的结果参数矩阵的行数和列数,多指定一个参数,来标识想获取的是行还是列,这个标识用1或2来表示,1代表想获取的是行数,2代表想获取的是列数:
>> A = ones(2,3);
>> size(A)
ans =
2 3
>> size(A,1)
ans = 2
>> size(A,2)
ans = 3
length函数,它获取的是矩阵中最大的那个维度的值,也就是说,对于一个m×n的矩阵,if m > n return m else return n:
>> A = ones(2,3);
>> B = ones(4,2);
>> length(A)
ans = 3
>> length(B)
ans = 4
获取矩阵指定行指定列的元素:
>> A = [1 2; 3 4; 5 6]
A =
1 2
3 4
5 6
>> A(3,2)
ans = 6
注:在Octave中下标从1开始
获取矩阵整行或整列的元素,某行或某列的全部元素可以用 : 号代替,返回的结果就是一个行向量或一个列向量:
>> A = [1 2; 3 4; 5 6]
A =
1 2
3 4
5 6
>> A(2,:)
ans =
3 4
>> A(:,1)
ans =
1
3
5
指定要获取的某几行或某几列的元素:
>> A = [1 2 3; 4 5 6; 7 8 9]
A =
1 2 3
4 5 6
7 8 9
>> A([1,2],:)
ans =
1 2 3
4 5 6
>> A(:,[1,3])
ans =
1 3
4 6
7 9
给矩阵的元素重新赋值。可以给指定行指定列的某一个元素赋值,也可以同时给某行或某列的全部元素一次性赋值:
>> A = [1 2; 3 4; 5 6]
A =
1 2
3 4
5 6
>> A(:,2) = [10, 11, 12]
A =
1 10
3 11
5 12
>> A(1,:) = [11 22]
A =
11 22
3 4
5 6
对矩阵进行扩展,比如增广矩阵,要在矩阵的右侧附上一个列向量:
>> A = [A, [100; 101; 102]]
A =
1 2 100
3 4 101
5 6 102
注:, 号也可以省略,使用空格也是一样的效果。即:A = [A [100; 101; 102]]
矩阵也可以进行组合:
>> A = [1 2; 3 4; 5 6]
A =
1 2
3 4
5 6
>> B = [11 12; 13 14; 15 16]
B =
11 12
13 14
15 16
>> [A B]
ans =
1 2 11 12
3 4 13 14
5 6 15 16
>> [A; B]
ans =
1 2
3 4
5 6
11 12
13 14
15 16
将矩阵的每一列组合在一起,转为一个更大的列向量:
>> A(:)
ans =
1
3
5
2
4
6
矩阵与矩阵的运算:
>> A
A =
1 2
3 4
5 6
>> B
B =
11 12
13 14
15 16
>> C
C =
1 1
2 2
矩阵相乘:
>> A*C
ans =
5 5
11 11
17 17
矩阵A的各个元素分别乘以矩阵B对应元素:
>> A .* B
ans =
11 24
39 56
75 96
注:点运算在这里可以理解为是对矩阵中每个元素做运算, 当一个实数与矩阵做乘法运算时,我们可以省略.直接使用*即可
Octave中内置的一些函数也是针对每个元素做运算的,比如对数运算、指数运算和绝对值运算等:
>> log([1; 2; 3])
ans =
0.00000
0.69315
1.09861
>> exp([1; 2; 3])
ans =
2.7183
7.3891
20.0855
>> abs([1; -2; 3])
ans =
1
2
3
矩阵的加法、转置和逆:
加法:
>> A = 1:5
A =
1 2 3 4 5
>> B = 6:10
B =
6 7 8 9 10
>> A + B
ans =
7 9 11 13 15
转置:
>> A = [1 2; 3 4; 5 6]
A =
1 2
3 4
5 6
>> A'
ans =
1 3 5
2 4 6
逆:
>> pinv(A)
ans =
-1.33333 -0.33333 0.66667
1.08333 0.33333 -0.41667
其他一些运算:
% a = [1 15 2 0.5],求最大值
>> val = max(a)
val = 15
% 求最大值,并返回最大值的索引
>> [val, idx] = max(a)
val = 15
idx = 2
% 矩阵对应元素的逻辑运算
>> a <= 1
ans =
1 0 0 1
>> find(a < 3)
ans =
1 3 4
% 计算之和
>> sum(a)
ans = 18.500
% 计算乘积
>> prod(a)
ans = 15
% 向下取整
>> floor(a)
ans =
1 15 2 0
% 向上取整
>> ceil(a)
ans =
1 15 2 1
% 生成一个随机矩阵,矩阵元素的值位于0-1之间
>> rand(3)
ans =
0.458095 0.323431 0.648822
0.481643 0.789336 0.559604
0.078219 0.710996 0.797278
% 矩阵按行上下对换
>> flipud(eye(4))
ans =
Permutation Matrix
0 0 0 1
0 0 1 0
0 1 0 0
1 0 0 0
控制语句和函数
for、while、if 语句,语句结束用end
% for语句
>> V = zeros(10,1);
>>> for i=1:10,
V(i) = 2^i;
end;
>> V
V =
2
4
8
16
32
64
128
256
512
1024
% while语句
>> V = zeros(10,1);
>> i = 1;
>> while i <= 5,
disp(V(i));
i = i+1;
end;
2
4
8
16
32
>> i = 1;
>> while true,
disp(V(i));
if i > 5,
break;
end;
i = i + 1;
end;
2
4
8
16
32
64
函数结束用end:
>> function y = squareNum(x)
y = x^2;
end;
>> squareNum(3)
ans = 9
在Octave中,定义一个函数需要使用function 关键字,然后紧跟在 function 后面的是函数的声明,包括返回值,函数名称和参数,之后换行来实现具体的函数功能。
Octave的函数不需要显示的返回语句,Octave会将函数第一行声明的返回值返回给调用方,因此,我们在函数体中只需将最终的计算结果赋给定义的返回值,比如上面例子中的y。
在Octave中,函数可以返回多个值:
>> function [y1, y2] = calVal(x)
y1 = x^2;
y2 = x^3;
end;
>> [a, b] = calVal(3)
a = 9
b = 27
也可以把函数写进文件中,然后加载实现函数。
进入octave后,cd到指定的目录下,这里我是把函数文件存在d盘下的文件中
cd D:\octave
之后你可以用pwd打印出当前目录的路径看看是否是在该文件下。
在该目录下新建一个文件名为“squareThisNumber.m”后缀是.m这样octave可以自动识别,双击后就会用notepad++自动打开,就可以编辑自己的函数。
注意:文件名要和函数名保持一致。
function y = squareThisNumber(x)
y = x^2;
函数的返回值是y,函数的自变量是x(这里只有一个返回值,可以有多个返回值),函数的主体是y = x^2
>> squareThisNumber(5)
ans = 25
这样就实现一简单求数平方的函数。
加载和保存数据
在上面一节中,介绍了如何在Octave的交互环境定义函数。但是大部分时候,我们都会将函数保存在文件中,从而在需要时可以随时调用。我们也能够在文件中存储数据,比如矩阵参数等,使用 load 命令可以将文件中的内容加载进来。
通常会比较常用的一些命令有如下几个:
显示当前的工作目录:
>> pwd
ans = D:\Octave
进到指定的目录:
>> cd C:\Windows
>> pwd
ans = C:\Windows
列出当前目录下的文件:
>> pwd
ans = D:\Octave
>> ls
featureX.dat priceY.dat
加载当前目录下的数据(也可以使用load函数):
>> load featuresX.dat
>> load pricesY.dat
查看当前工作空间下都有哪些变量:
>> who
Variables in the current scope:
ans featuresX pricesY
查看详细的变量信息:
>> whos
Variables in the current scope:
Attr Name Size Bytes Class
==== ==== ==== ===== =====
ans 1x13 13 char
featuresX 3x2 48 double
pricesY 3x1 24 double
Total is 22 elements using 85 bytes
>> featuresX % 查看加载进来的变量
featuresX =
123 1
456 2
789 3
>> pricesY
pricesY =
11
22
33
clear 命令可以清除一个变量,如果后面没有跟具体的变量名,则会清空全部变量:
>> clear ans
保存数据到指定的文件,它的语法格式是这样的:
save {file_name} {variables}
>> V = pricesY(1:2) % 获取第一列的前两个元素
V =
11
22
% 保存变量V到hello.mat文件
>> save hello.mat V;
在保存的时候也可以指定一种编码格式,比如下面的例子指定了 ascii 编码,如果不指定,数据将会被保存为二进制格式。
>> save hello.txt V -ascii
注:假如你使用pwd命令发现当前的工作目录是A,同时你实现了一个函数someFunc,存储在文件someFunc.m中,如果这个someFunc.m文件不在A目录,那么在使用someFunc函数之前,需要先调用load方法将其加载进来,反之可以直接使用。
绘制图形
以绘制一个sin函数曲线和一个cos函数曲线为例,来说明如何在Octave中绘图。
先来定义数据:
>> t = [0:0.01:0.98];
>> y1 = sin(2*pi*4*t);
>> y2 = cos(2*pi*4*t);
这里的t我们看做是横轴,y1看做是纵轴,然后调用plot函数:
>> plot(t, y1);
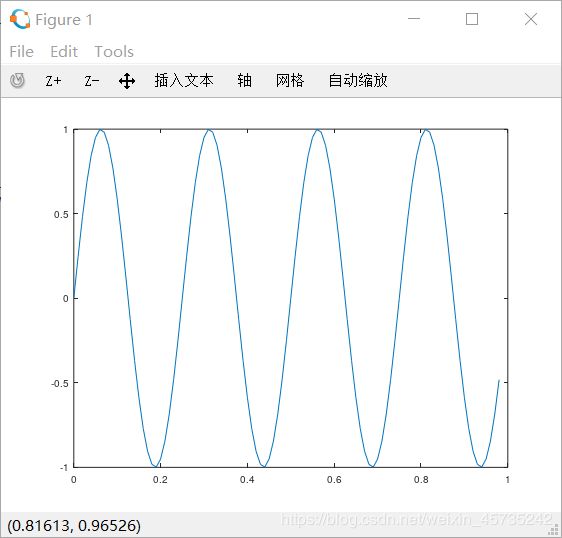
接下来我们继续在这个图像上绘制cos函数。这时需要用到hold on命令,它的作用是将新图像画在旧图像上面,而不是覆盖旧图像。
为了区分sin函数,我们将cos函数的曲线用红色标识:
>> hold on;
>> plot(t,y2, 'r');
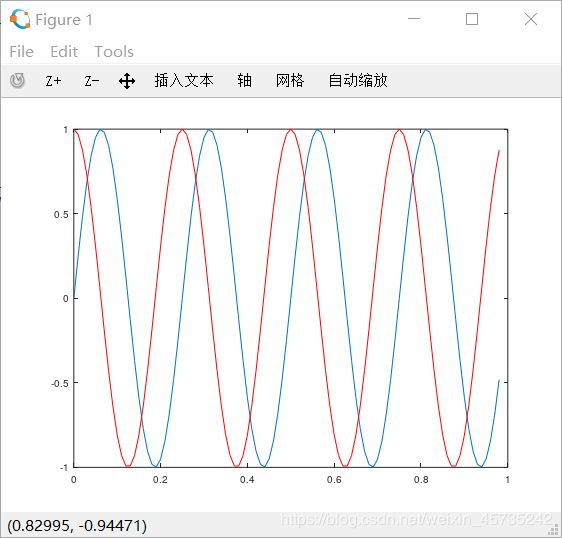
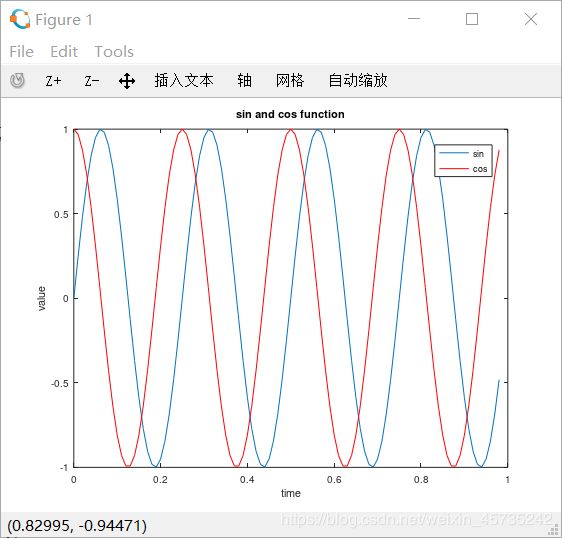
图形有了,最后一步就是标明横轴和纵轴分别代表的含义,再给图形起一个有意义的名字:
>> xlabel('time'); % 指定X轴的名称
>> ylabel('value'); % 指定Y轴的名称
>> legend('sin', 'cos'); % 标识第一条曲线是sin,第二条曲线是cos
>> title('sin and cos function'); % 给图片附一个标题
>> print -dpng 'sin_cos.png'
在绘图中,想重新绘图,怎么办呢?也很简单,只要输入clf命令,Octave会将绘图框中的图形全部清空。
不论何时,输入close命令,Octave会关闭该绘图窗口。
>> clf;
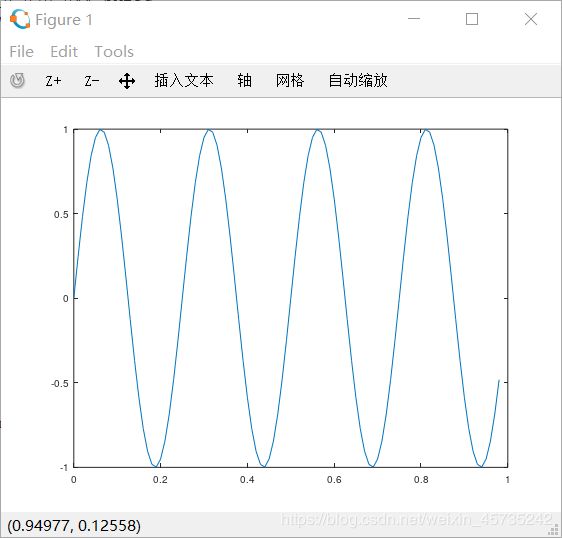
>> figure(1);
>> plot(t,y1);
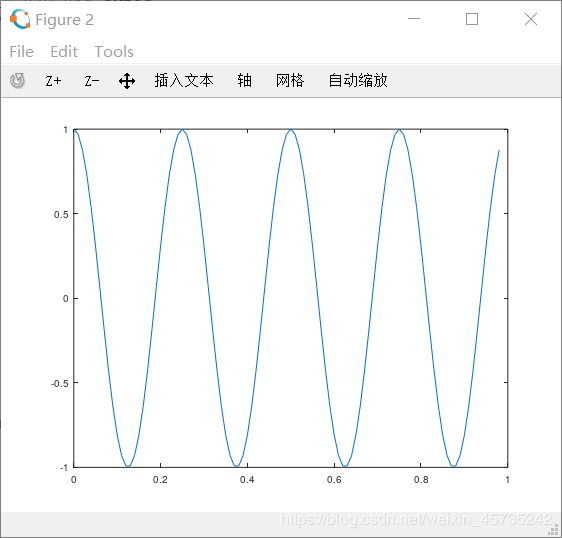
>> figure(2);
>> plot(t,y2);
也可以把窗口分成若干个的格子:
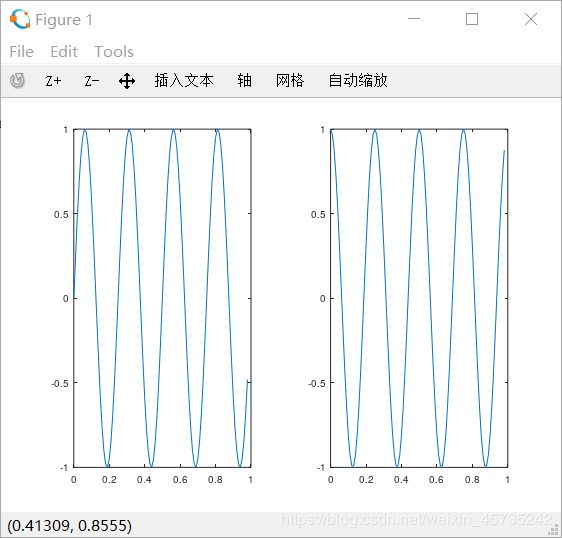
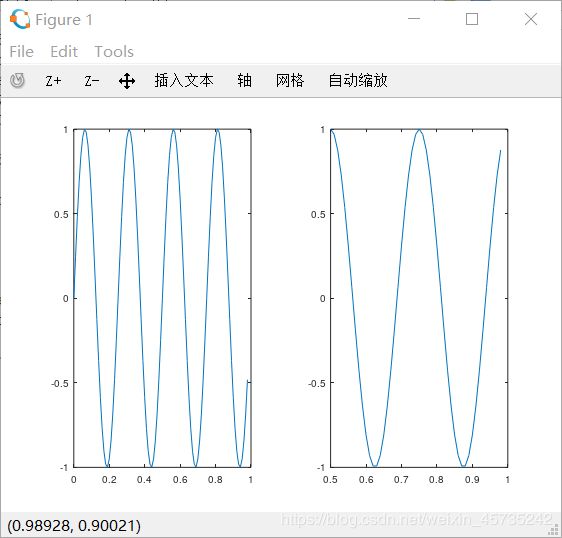
>> subplot(1,2,1); %这样做是把窗口分成一个1*2的格子,使用第一个格子;
>> plot(t,y1);
>> subplot(1,2,2);
>> plot(t,y2);
>> axis(0.5 1 -1 1) %调整右边图像的x,y坐标的范围。
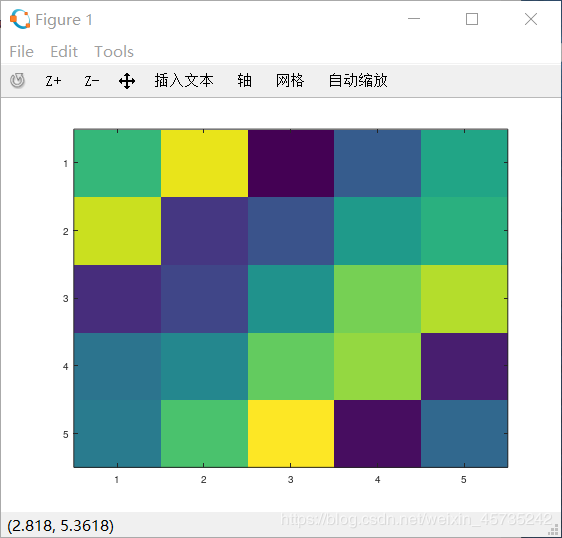
>> A = magic(5);
>> imagesc(A); %生成一个5*5 的色块