Octave快速入门
Octave是一种编程语言,旨在解决线性和非线性的数值计算问题,其语法与Matlab非常接近。
目录
- 下载安装
- 基本操作
- 数学运算
- 逻辑运算
- 变量
- 向量和矩阵
- 注释
- 数据处理
- 加载数据
- 存储数据
- 操作数据
- 数据计算
- 数据可视化
- 控制语句
- 向量化
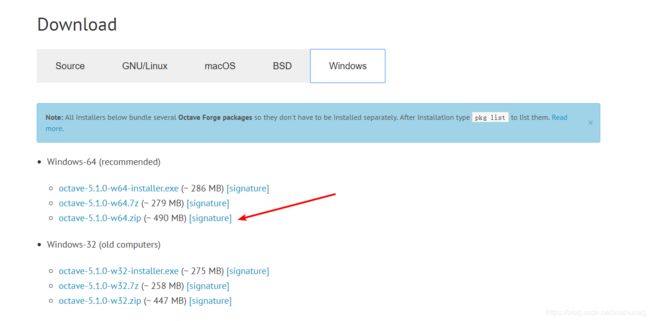
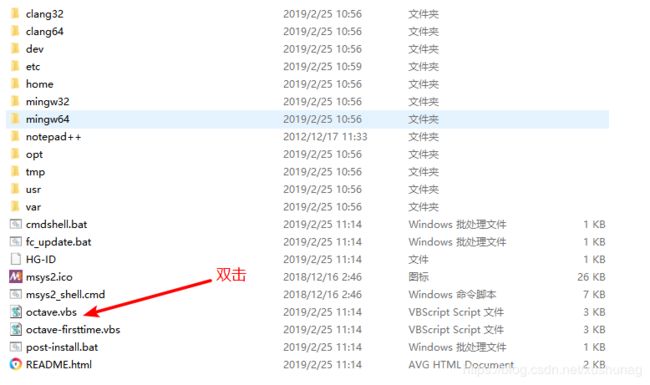
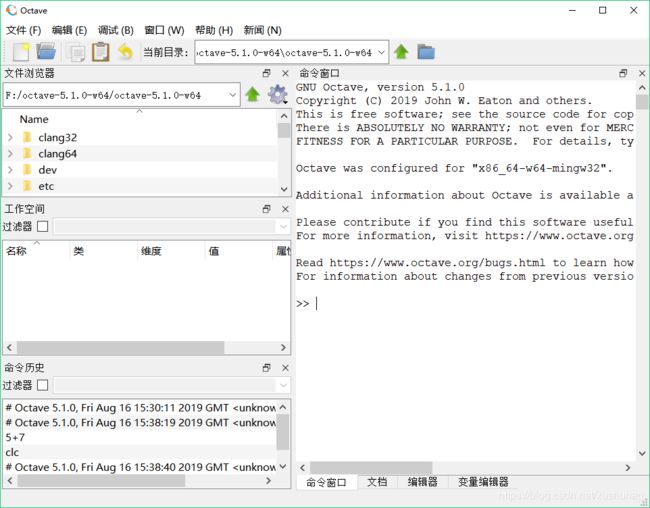
下载安装
基本操作
数学运算
加法
>> 5+6
ans = 11
减法
>> 3-2
ans = 1
乘法
>> 5*8
ans = 40
除法
>> 1/2
ans = 0.50000
幂次方
>> 2^6
ans = 64
逻辑运算
相等
>> 1==2
ans = 0
不等
>> 1~=2
ans = 1
与
>> 1&&0
ans = 0
或
>> 1||0
ans = 1
异或
>> xor(1,0)
ans = 1
变量
变量赋值
>> a=3
a = 3
变量赋值 不直接输出
>> b=4;
>>
输出
(1)
>> a=pi;
>> a
a = 3.1416
(2)
>> disp(a)
3.1416
(3)保留小数点后2位
>> disp(sprintf('2 decimals: %0.2f',a))
2 decimals: 3.14
(4)显示默认位数
>> format long
>> a
a = 3.141592653589793
(5)默认打印少量小数点后位数
>> format short
>> a
a = 3.1416
向量和矩阵
矩阵
>> A=[1 2; 3 4; 5 6]
A =
1 2
3 4
5 6
生成元素全为0的矩阵
>> w=zeros(4,3)
w =
0 0 0
0 0 0
0 0 0
0 0 0
生成元素全为1的矩阵
>> ones(2,3)
ans =
1 1 1
1 1 1
>>
生成随机矩阵(元素为0-1之间的随机值)
>> w=rand(2,3)
w =
0.494072 0.222685 0.750169
0.150811 0.016189 0.062860
生成单位矩阵
>> eye(4)
ans =
Diagonal Matrix
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
矩阵大小
>> A
A =
1 2
3 4
5 6
>> size(A)
ans =
3 2
向量
行向量
>> v=[1 2 3]
v =
1 2 3
列向量
>> v=[1; 2; 3]
v =
1
2
3
从1开始 步长为0.1 增长到2
>> v=1:0.1:2
v =
1.0000 1.1000 1.2000 1.3000 1.4000 1.5000 1.6000 1.7000 1.8000 1.9000 2.0000
>>
返回最大维度的大小
>> length([1;2;3;4;5;6])
ans = 6
注释
>> %This is a comment
>>
数据处理
加载数据
显示当前路径
>> pwd
ans = F:\octave-5.1.0-w64\octave-5.1.0-w64
加载数据
>> load featuresX.dat
>> load priceY.dat
显示当前工作空间所有变量
>> who
显示详细的变量信息
>> whos
存储数据
将Y的前10个数据赋给v
>> v=priceY(1:10)
将变量存储至硬盘(使变量v保存为一个名为hello.mat的文件)
>> save hello.mat v;
将数据存储成用accii编码的文档
>> save hello.txt v -ascii
操作数据
索引
>> A=[1 2; 3 4; 5 6]
A =
1 2
3 4
5 6
>> A(3,2)
ans = 6
某一行 / 列所有元素
>> A(2,:)
ans =
3 4
>> A(:,2)
ans =
2
4
6
某一列赋值
>> A(:,2)=[10; 11; 12]
A =
1 10
3 11
5 12
添加一列
>> A=[A,[100; 101; 102]];
>> A
A =
1 10 100
3 11 101
5 12 102
将A中所有元素放入一个单独的列向量
>> A(:)
ans =
1
3
5
10
11
12
100
101
102
矩阵的组合
>> C=[A B]
C =
1 2 11 12
3 4 13 14
5 6 15 16
>> C=[A;B]
C =
1 2
3 4
5 6
11 12
13 14
15 16
删除变量a
>> clear a
清除工作空间中的所有变量
>> clear
数据计算
>> A=[1 2; 3 4; 5 6]
A =
1 2
3 4
5 6
>> B=[11 12; 13 14; 15 16]
B =
11 12
13 14
15 16
>> C=[1 1; 2 2]
C =
1 1
2 2
矩阵的乘法
>> A*C
ans =
5 5
11 11
17 17
矩阵的点乘(.表示针对元素的运算)
>> A.*B
ans =
11 24
39 56
75 96
矩阵的乘方(.表示针对元素的运算)
>> A.^2
ans =
1 4
9 16
25 36
矩阵的倒数(.表示针对元素的运算)
>> 1./A
ans =
1.00000 0.50000
0.33333 0.25000
0.20000 0.16667
对所有元素进行求对数运算
>> v=[1;2;3]
v =
1
2
3
>> log(v)
ans =
0.00000
0.69315
1.09861
以e为底数 以v中元素为指数的幂运算
>> exp(v)
ans =
2.7183
7.3891
20.0855
对矩阵中元素求相反数
>> -v
ans =
-1
-2
-3
对矩阵中元素求绝对值
>> abs([-1;-2;-3])
ans =
1
2
3
矩阵中各个元素加1
>> v+1
ans =
2
3
4
>> v+ones(length(v),1)
ans =
2
3
4
矩阵的转置
>> A
A =
1 2
3 4
5 6
>> A'
ans =
1 3 5
2 4 6
矩阵的逆
>> A=[8 1 6;3 5 7;4 9 2]
A =
8 1 6
3 5 7
4 9 2
>> pinv(A)
ans =
0.147222 -0.144444 0.063889
-0.061111 0.022222 0.105556
-0.019444 0.188889 -0.102778
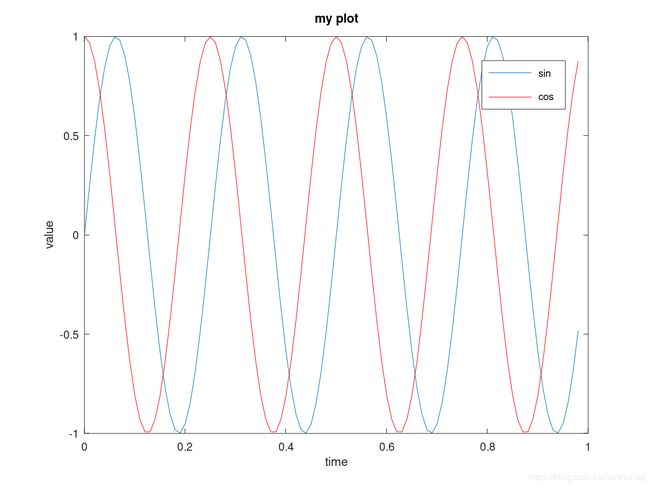
数据可视化
图像的绘制、坐标轴、图例、保存、关闭
>> t=[0:0.01:0.98];
>> y1=sin(2*pi*4*t);
>> plot(t,y1);
>> t=[0:0.01:0.98];
>> y1=sin(2*pi*4*t);
>> y2=cos(2*pi*4*t);
>> plot(t,y1);
>> hold on;
>> plot(t,y2,'r');
>> xlabel('time')
>> ylabel('value')
>> legend('sin','cos')
>> title('my plot')
>> cd 'C:\Users\lenovo\Desktop';print -dpng 'myplot.png'
>> close
>> subplot(1,2,1);
>> plot(t,y1);
>> subplot(1,2,2)
>> plot(t,y2);
>> clf;
控制语句
for
>> v=zeros(10,1);
>> for i=1:10,
v(i)=2^i;
end;
>>
>> v
v =
2
4
8
16
32
64
128
256
512
1024
>>
while
>> i=1;
>> while i<=5,
v(i)=100;
i=i+1;
end;
>> v
v =
100
100
100
100
100
64
128
256
512
1024
>>
if
>> i=1;
>> while true,
v(i)=999;
i=i+1;
if(i==6),
break;
end;
end;
>> v
v =
999
999
999
999
999
64
128
256
512
1024
if-else
>> v(1)=2;
>> if v(1)==1,
disp('The value is one');
elseif v(1)==2,
disp('The value is two');
else
disp('The value is not noe or two.');
end;
The value is two
向量化
(简单、高效的处理方式—向量化)
举例:
h θ ( x ) = ∑ j = 0 n θ j x j = θ T x h_θ(x)=\displaystyle\sum_{j=0}^nθ_jx_j=θ^Tx hθ(x)=j=0∑nθjxj=θTx
(1)非向量化实现
>> prediction=0.0;
>> for j=1:n+1,
prediction=prediction+theta(j)*x(j)
end;
(2)向量化实现
>> prediction=theta'*x;