注,有疑问 加QQ群..[174225475].. 共同探讨进步
有偿求助请 出门左转 door , 合作愉快
信用评分是指根据客户的信用历史资料,利用一定的信用评分模型,得到不同等级的信用分数。根据客户的信用分数, 授信者可以分析客户按时还款的可能性。据此, 授信者可以决定是否准予授信以及授信的额度和利率
原理
A/B系数计算
Score= A - B * log(odds)
Score + pdo = A - B * log(odds/2)
B = pdo / log(2)
A = Score + B* log(odds)
odds - 坏好比 , 目标变量值 1 的占比 除以 0 的占比
pdo - odds 变化时 Score 得分的上下浮动差
初始计算A/B值时, odds 为整体数据的坏好比,即
odds = P_bad / (1-P_bad)
一般设定 Score 为600 ; Odds 减半时,Score +20,假设初始 odds = (p/1-p)=0.2/0.8=0.25 则
B = 20 / log(2)=28.8539
A = 600 + 28.8539 * log(0.25) = 560逻辑回归系数转化
log(odds)=Beta_0+Beta_1 * x_1+Beta_2 * x_2+Beta_3 * x_3+...
Score = A - B * log(odds)
= A - B * (Beta_0+Beta_1 * x_1+Beta_2 * x_2+Beta_3 * x_3+...)
= A - B * Beta_0-B * Beta_1 * x_1-B * Beta_2 * x_2-B * Beta_3 * x_3...
=(A - B * Beta_0)-(B * Beta_1) * x_1-(B * Beta_2) * x_2-(B * Beta_3) * x_3...
注: x_i = woe_i
案例应用
1. 数据读取
library(openxlsx)
library(data.table)
# 读取各网点的日运营明细
data1<-read.xlsx("../data1.xlsx",sheet=1)
data2 <- data.table(data1)[,lapply(.SD,sum),
keyby=.(UID,month),
.SDcols=names(data1)[4:17]]
# 列名称中不能带'.',若有则需要修改,考虑到作图名称过长也改掉
colnames(data2)[3:7]=c('lin_zhi','lin_zhuan','kuasheng','G_G','G_M')
colnames(data2)[ncol(data2)-c(2,1)] <- c('pingtai','quantity')
2. 数据清洗
2.1 NA 处理
2.1.1 NA 的列处理方式
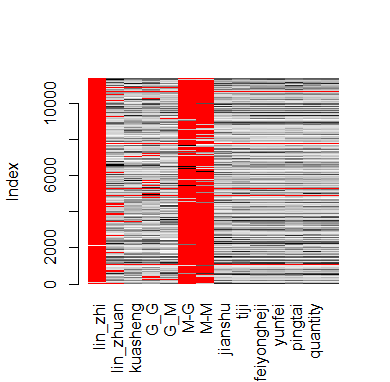
VIM::matrixplot(res1)
na1 <- as.data.frame(sapply(res1,function(x){sum(is.na(x))/length(x)}))
colnames(na1)='per1';na1$col1 <- rownames(na1)
na1[order(-na1$per1),]
per1 col1
lin_zhi 0.99480405 lin_zhi
M-G 0.90656099 M-G
M-M 0.83540291 M-M
lin_zhuan 0.09749009 lin_zhuan
G_G 0.07476882 G_G
G_M 0.04720387 G_M
... ...
res10 <- res1[,-c(1,6,7)]
2.1.2 NA 的行处理方式
na_cnt1 <- apply(res10,1,function(x)sum(is.na(x)))
table(na_cnt1)
na_cnt1
0 1 2 3 4 5 6 11
9416 1372 309 31 44 4 4 175
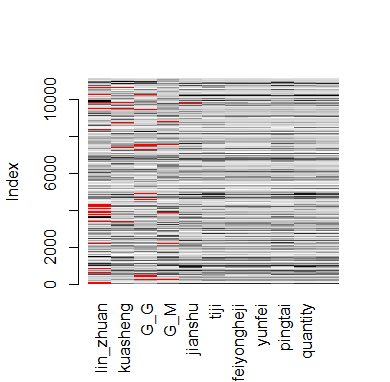
res101 <- res10[-which(na_cnt1>=round(ncol(res10)/3)),]
VIM::matrixplot(res101)
2.1.3 其他 NA 的处理方式
- 自动填充
rcaret::knnImputation() - 均值替代
rx[is.na(x)] = mean(x, na.rm=TRUE) - 全部用 0 填充
本案例结合实际情况,采集 0 填充的方案
res11 <- res101[,lapply(.SD,function(x) ifelse(is.na(x),0,x))]
2.2 异常值处理
异常值检测 可以用 rquantile(x,c(0.25,0.75)) +/- 1.5(or 3) * diff(quantile(x,c(0.25,0.75))) 的标准来完成
3. 共线性诊断处理和变量筛选
# --- 多重共线性诊断
corr1 <- cor(res101[,!'clus1'])
kappa(corr1,exact = TRUE)
# 条件数<100,则认为多重共线性的程度很小,
# 若100<=条件数<=1000,则认为存在中等程度的多重共线性,
# 若条件数>1000,则认为存在严重的多重共线性.
# lasso变量筛选
# 如有疑问 请咨询QQ群 174225475
head(res11)
4. WoE 计算
indx1 <- sample(c(0,1),nrow(res11),prob = c(0.3,0.7),replace = TRUE)
train1 <- res11[indx1==1,]
test1 <- res11[indx1==0,]
dat <- data.frame(train1) # train data
y='clus1' # target var
var_d <- c() # category var
var_c <- c() # numeric var
if(length(var_d1)==0){
var_d = NULL
}else{var_d = var_d1}
if(length(var_c1)==0){
var_c = NULL
}else{var_c = var_c1}
fit_data <- dat # testdata
source('./woe_repalce.R') # 调用 woe 计算函数
# woe_replace函数, 请咨询QQ群 174225475
library(smbinning)
woe_info1 <- woe.replace(dat,var_c,var_d,y,fit_data)
woe1 <- woe_info1[[1]] # woe 分值
(rules1 <- woe_info1[[2]]) # 各变量内分组与woe分值对应关系
Cutpoint WoE varIndex
1 <= 0.1139 -5.9691 jiesuanshouru
2 <= 0.356 -2.3566 jiesuanshouru
3 <= 0.5561 -1.0874 jiesuanshouru
4 <= 0.8008 0.2356 jiesuanshouru
5 <= 1.0811 1.6840 jiesuanshouru
6 <= 1.3079 2.7690 jiesuanshouru
... ...
5. 最终得分计算及评分规则整理
5.1 计算系数 A/B
> (pdo <- 30)
[1] 30
> (B <- pdo/log(2))
[1] 43.28085
> (odds <- table(train1$clus1)[2]/table(train1$clus1)[1])
1
0.2579551
> (SC <- 600)
[1] 600
> (A <- SC + B*log(odds))
1
541.3558
5.2 利用 WoE 值重新建立 logistic 模型计算 各项系数
实际操作中, 因变量的分布是极度不平衡的, 因此在建模时就有了要不要人工设定 weights 参数对建模数据进行样本比例矫正, 以下是两种方案(设置/不设置weights)的比较
> woe2 <- data.frame(cbind(woe1,clus1=train1$clus1))
> lgc3 <- glm(clus1~.,data=woe2,
family = binomial(link = 'logit'))
> lgc_res3 <- predict(lgc3,data.frame(woe1),type = 'response')
> table(ifelse(lgc_res3 >0.5,1,0),train1$clus1)
0 1
0 6100 90
1 91 1507
> library(ModelMetrics)
> auc(ifelse(lgc_res3 >0.5,1,0),train1$clus1)
[1] 0.9642571
# ------------------
> lgc3 <- glm(clus1~.,data=woe2,weights = ifelse(woe2$clus1>0,5,1),
+ family = binomial(link = 'logit'))
> lgc_res3 <- predict(lgc3,data.frame(woe1),type = 'response')
> table(ifelse(lgc_res3 >0.5,1,0),train1$clus1)
0 1
0 5991 18
1 200 1579
> library(ModelMetrics)
> auc(ifelse(lgc_res3 >0.5,1,0),train1$clus1)
[1] 0.9422909
> woe_info2 <- woe.replace(dat,var_c,var_d,y,
+ fit_data = data.frame(test1))
> woe3 <- woe_info2[[1]]
> lgc_res4 <- predict(lgc3,data.frame(woe3),type = 'response')
> table(ifelse(lgc_res4 >0.5,1,0),test1$clus1)
0 1
0 534 10
1 29 18
添加了 weights 参数, 模型对 违约客户 的预测准确率会更高, 但整体AUC 会受影响, 因此在建模时可根据 业务的实际需求进行 weights 参数的取舍
5.3 WoE 向实际得分转化及其规则整理
# --- train1 样本总得分计算
coef1 <- lgc3$coefficients
(BaseSC <- A-B*coef1[1])
Tsc1 <- BaseSC + woe1 %*% coef1[-1]
# ---得分转化规则梳理
rules1$coef1 <- coef1[rules1$varIndex]
rules1$sc1 <- with(rules1,WoE*coef1)
# --- 分值分布情况
library(dplyr)
rules1 %>%
group_by(varIndex) %>%
summarise(max1=max(sc1),
min1=min(sc1),
mean1=mean(sc1))
# A tibble: 7 x 4
varIndex max1 min1 mean1
1 feiyongheji 2.4498204 -3.176858 -0.12697315
2 jianshu 2.9163435 -3.223899 0.18207080
3 jiesuanshouru 2.8838985 -3.500189 0.29030440
4 pingtai 3.4201266 -5.301336 -0.02456898
5 quantity 0.9789534 -1.492049 -0.11555953
6 tiji 2.8583949 -3.338300 -0.08009086
7 yunfei 2.4681047 -3.475437 -0.14391316
# --- 规则展示
> rules1[,.(varIndex,Cutpoint,sc1)]
varIndex Cutpoint sc1
1: jiesuanshouru <= 0.1139 -3.50018886
2: jiesuanshouru <= 0.356 -1.38187416
3: jiesuanshouru <= 0.5561 -0.63763471
4: jiesuanshouru <= 0.8008 0.13815223
5: jiesuanshouru <= 1.0811 0.98747182
6: jiesuanshouru <= 1.3079 1.62369921
7: jiesuanshouru <= 1.4988 2.20891113
8: jiesuanshouru > 1.4988 2.88389855
9: feiyongheji <= -0.449 -3.17685829
10: feiyongheji <= 0.2052 -1.85452835
11: feiyongheji <= 0.4717 -0.89196384
12: feiyongheji <= 0.7499 -0.19168770
13: feiyongheji <= 1.0887 0.92124707
14: feiyongheji <= 1.4839 1.85515871
15: feiyongheji > 1.4839 2.44982037
16: yunfei <= -0.5582 -3.47543677
17: yunfei <= 0.2745 -1.86611915
... ...