基于PCA的ORL人脸识别---Python
PCA的理论知识已经有很多博客都做了清晰的解释,主要概括为找到投影的面使得类间误差最大,转化为找到构建的协方差矩阵的特征值与特征向量,再在新的投影方向上(特征向量)上投影,构建数据库和带检索人脸进行比对,得到相似度最高的视为查询结果。下面针对ORL人脸数据库进行PCA的识别。。。
PCA算法:
设有m条n维数据:
1)将原始数据按列组成n行m列矩阵X
2)将X的每一行(代表一个属性字段)进行零均值化,即减去这一行的均值
3)求出协方差矩阵
4)求出协方差矩阵的特征值及对应的特征向量
5)将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P
6)Y=PX即为降维到k维后的数据
方案设计:
1.将ORL人脸数据库的40位志愿者的10张图片,使用10折交叉验证。每个人依次取出一张作为验证数据,进行10轮验证,最后得到准确率的均值。对于每次运算,训练集大小为360张图片,验证集大小为40张图片。对每张图片,将其展开为一维向量Xi;即训练集X=(X1, X2,…X360)维度为(10304,360);
2.求取X每行的均值向量u,并将其与X相减,进行零均值化,得到C=(X1-u, X2-u,…,X360-u);
3.构建协方差矩阵 CCT;
4.求解协方差矩阵的特征值,选取最大的k个,求出对应的k个特征向量,并将其按列排成变换矩阵P,其维度为(10304*k);
5.计算训练集的图片在上述特征向量下的投影,即为Yi = PT(Xi-u),作为查找集;
6.将待识别的图片做以上相同投影运算得到Z;
7.遍历搜索查找集,满足min||Yi-Z||条件的即待识别图片与Yi对应图片属于一类;即找到待识别照片的主人。
其中构建的协方差矩阵CCT进行特征值与特征向量求解时非常耗时,故构造CTC进行特征值和特征向量的求取,最后通过将求得的特征向量左乘C即可得到CTC的特征向量。
代码实现:
import cv2
import numpy as np
import glob
# 预处理 构建数据矩阵
images = glob.glob(r'.\ORL\*.bmp')
X = []
for img in images:
img = cv2.imread(img, 0)
temp = np.resize(img, (img.shape[0] * img.shape[1], 1))
X.append(temp.T)
X = np.array(X).squeeze().T
# 10轮
correct_sum = 0
for epoch in range(10):
# 10折交叉验证 数据划分
train_data = X[:, [x for x in list(range(X.shape[1])) if x not in list(range(epoch, X.shape[1], 10))]]
test_data = X[:, list(range(epoch, X.shape[1], 10))]
# train
u = np.sum(train_data, axis=1) / train_data.shape[1] # 求均值向量
''' 平均脸
u = np.array(u, dtype='uint8')
average_face = np.resize(u, (img.shape[0], img.shape[1]))
cv2.imshow('Avarage Face', average_face)
cv2.waitKey(0)
'''
u = u[:, np.newaxis]
C = train_data - u # 中心化后数据矩阵
Covariance = np.dot(C.T, C) # 构建协方差矩阵,一般为C .* C.T,但是构造这种类型可减少运算量
eigvalue, eigvector = np.linalg.eig(Covariance) # 由协方差矩阵求解特征值、特征向量
real_eigvector = np.dot(C, eigvector) # 通过之前的构造来恢复真正协方差矩阵对应的特征向量
sort = np.argsort(-eigvalue) # 将特征值从大到小怕排序,得到排序后对于原索引
P = real_eigvector.T[sort[0:100]] # 对于排序构造特征向量,取前面较大权重值
Y = []
for i in range(train_data.shape[1]):
temp = train_data[:, i, np.newaxis]
Y.append(np.dot(P, temp - u)) # 构建每幅图像投影后的值,构造查找表
# test
correct = 0
for index in range(test_data.shape[1]):
img_test = test_data[:, index, np.newaxis] # 从测试集提取单张人脸
Result = np.dot(P, img_test - u) # 计算待识别的人脸的投影
a = np.sum(abs(Y - Result), axis=1).argmin() # 遍历搜索匹配
if index*9 <= a < (index+1)*9: # 若索引在宽度为9的区间内则为该人脸,视为匹配正确
correct += 1
print('Epoch{} correct rate: {}%'.format(epoch, correct/40*100))
correct_sum += correct
print('Final correct rate: {}%'.format(correct_sum/4))
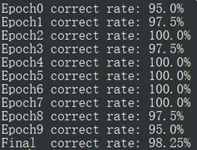
运算结果:
图一 识别结果 图二 平均脸
结果分析:
通过10折交叉验证,最后得到的验证准确度为98.5%,为较好水平。即通过少量的样本可以得到很好的结果,说明PCA在降维上拥有很好的效果,较好的保留了主要特征。