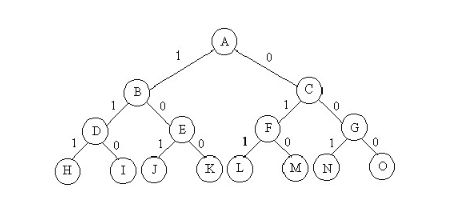
回溯详解以及与 DFS 算法的关联

概述

回溯法是一种选优搜索法（试探法），被称为通用的解题方法，这种方法适用于解一些组合数相当大的问题。通过剪枝（约束+限界）可以大幅减少解决问题的计算量（搜索量）。

深度优先搜索（Depth-First-Search，DFS）是一种用于遍历或搜索树或图的算法。沿着树的深度遍历树的节点，尽可能深的搜索树的分支。当节点v的所在边都己被探寻过，搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源节点可达的所有节点为止。如果还存在未被发现的节点，则选择其中一个作为源节点并重复以上过程，整个进程反复进行直到所有节点都被访问为止。

回溯和深度优先搜索的区别

回溯是一种更通用的算法。可以用于任何类型的结构，其中可以消除域的部分 ——无论它是否是逻辑树。

深度优先搜索是与搜索树或图结构相关的特定回溯形式。它使用回溯作为其使用树的方法的一部分，但仅限于树/图结构。

回溯和 DFS 之间的区别在于回溯处理隐式树而 DFS 处理显式树。这似乎微不足道，但它意味着很多。当通过回溯访问问题的搜索空间时，隐式树在其中间被遍历和修剪。然而对于 DFS 来说，它处理的树/图是明确构造的，并且在完成任何搜索之前已经抛出了不可接受的情况，即修剪掉了。

因此，回溯是隐式树的 DFS，而 DFS 是回溯而不修剪。

回溯法的基本思想：

1. 针对所给问题，定义问题的解空间；
2. 确定易于搜索的解空间结构；
3. 以深度优先方式搜索解空间，并在搜索过程中用剪枝函数避免无效搜索。

典型的解空间树

第一类解空间树：子集树

当问题是：从 n 个元素的集合 S 中找出满足某种性质的子集时相应的解空间树称为子集树。遍历子集树，时间复杂度 O(2^n)。

如果解的长度是不固定的，那么解和元素顺序无关，即可以从中选择 0 个或多个。例如：幂集、子集、迷宫…

如果解的长度是固定的，那么解和元素顺序有关，即每个元素有一个对应的状态。例如：n 括号问题，八皇后，…

适用于：幂集、子集、0-1 背包、装载、n 括号问题、八皇后、迷宫、…

子集树模版

以求解子集问题为模版，后续会更新利用回溯法求解的各类经典问题。

a = [1, 2, 3, 4]
subset_list = []#一组解
subset = [] #一个解，用于存放a[i]的选择状态：1-选择，0-不选
target = 8  #约束条件


def conflict(k, subset: list):
    '''
    剪枝函数：和小于8的子集
    :param k:
    :param subset:
    :return:
    '''
    global a,target

    if k == 0:
        return True

    # 根据部分解，构造部分集
    s = [x[0] for x in filter(lambda x: x[1] != 0, zip(a[:k + 1], subset[:k + 1]))]
    if sum(s) < 8:
        return True
    return False


def dfs(k):
    '''

    :param k: 第 k 个元素
    :return:
    '''
    global a, subset_list, subset

    if k >= len(a):
        subset_list.append([a[k] for k,v in enumerate(subset) if v != 0])#保存一个子集
    else:
        for i in range(2):# 遍历元素 a[k] 的两种选择状态:1-选择，0-不选
            subset.append(i)
            if conflict(k,subset):  #剪枝，当注释掉该条件，得到的结果为所有的子集
                dfs(k + 1)
            subset.pop()    #回溯


dfs(0)
print(subset_list)

再分析一下 n 括号问题，求括号排列的所有可能性。

n = 4

brackets_list = []

def conflict(s,sublist):
    '''
    剪枝函数：括号排列是有条件约束的，n对括号，所以左右括号的个数都不能超过n；排列过程中，当前排列中左括号数目不小于右括号，否则会出现这样的情况：'())(()'
    :param s:
    :param sublist:
    :return:
    '''
    global n
    if sublist.count(s) <= n and sublist.count('(') >= sublist.count(')'):
        return True
    return False

def dfs(m,sublist, brackets_list: list):
    '''
    括号排列自身是有约束条件的，第一必须为左括号，最后一个必须为右括号
    :param m:
    :param sublist:
    :param brackets_list:
    :return:
    '''
    if m == 1 and sublist[-1] == ')':#规定第一个为左括号，最后一个为右括号
        brackets_list.append(sublist)
    else:
        for i in range(2):#当根节点为左括号时，下一个节点的值：'('-1,')'-0
            s = '(' if i == 1 else ')'
            sublist += s
            if conflict(s, sublist):#剪枝
                dfs(m-1, sublist, brackets_list)
            sublist = sublist[:-1]#回溯

dfs(2*n,'(',brackets_list)
print(brackets_list)

如下列结构图一样，在实际排列过程中通过约束条件进行限制。

关于 n 对括号排列问题，从字面意思看以为该问题的解空间是排列树，但是由于括号的限制性，在实际分析过程中，我们可以将其按照子集树的形式处理。n 对括号排列，它的每个解的长度都为 2*n，这一点同八皇后问题是一致的。

第二类解空间树：排列树

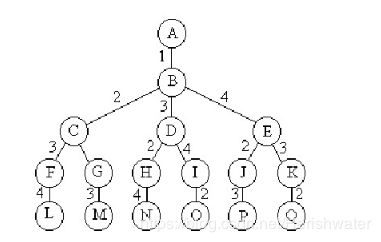
解空间是由 n 个元素的排列形成，也就是说 n 个元素的每一个排列都是解空间中的一个元素，那么，最后解空间的组织形式是排列树。遍历排列树，时间复杂度O(n!)。

适用于：旅商问题、n 个元素全排列 …

'''求[1,2,3,4]的全排列'''

a = [1,2,3,4]
results = []#一组解
ans = [0]*len(a)#用来标记a列表中的元素是否被取用
index_list = [0]*len(a)#排列组合中元素在列表a中的索引值，即为一个解

#暂无剪枝函数
def conflict():
    pass

def dfs(k):
    global a,results,ans

    if k >= len(a):
        results.append([a[i] for i in index_list])
        # results.append(a[:])
    else:
        for i in range(len(a)):
            if ans[i] == 0:#如果ans[i]为0，说明列表a中索引为i的元素还未放入到解中
                ans[i] = 1
                index_list[k] = i#将索引值i放入到解中
                dfs(k+1)
                ans[i] = 0#回溯

dfs(0)
print(results)

关于元素排列问题的扩展，分为字符串的全排列和列表的全排列。

1. 字符串的全排列

   s = 'abc'
   temp = ''
   
   s_set = set([])
   
   def pailie(s, temp):
       '''
       给定字符串，列出它的所有排列组合
       :param s:字符串
       :param temp:一个解
       :return:
       '''
       if len(s) == 0:
           s_set.add(temp)
           return
   
       for i in range(len(s)):
           new_s = s[0:i] + s[i+1:len(s)]
           pailie(new_s, temp+s[i])
   
   if __name__ == '__main__':
       pailie(s, temp)
       print(s_set)
       print(len(s_set))
   

2. 列表的全排列

   import copy
   
   s_list = ['a','b','c']
   ans = []
   results = set([])
   
   def dfs(s_list:list,ans):
       '''
       给定列表，列出所有排列组合
       :param s_list: 列表
       :param ans: 列表类型——解
       :return:
       '''
       if len(s_list) == 0:
           results.add(''.join(ans))
           return
       else:
           for i in range(len(s_list)):
               x =s_list.pop(i)
               new_ans = copy.copy(ans)#浅拷贝保证每次回溯回来的ans，都是上一次的值集
               new_ans.append(x)
               dfs(s_list,new_ans)
               s_list.insert(i,x)#回溯
   
   def dfs2(s_list:list,ans):
       if len(s_list) == 0:
           results.add(''.join(ans))
           return
   
       for i in range(len(s_list)):
           new_s = s_list[0:i] + s_list[i+1:len(s_list)]
           new_ans = copy.copy(ans)
           new_ans.append(s_list[i])
           dfs2(new_s,new_ans)#类似于字符串排列的实现方式
   
   def dfs3(s_list:list,ans):
       if len(s_list) == 0:
           results.add(''.join(ans))
           return
   
       for i in range(len(s_list)):
           new_s = s_list[0:i] + s_list[i+1:len(s_list)]
           ans.append(s_list[i])
           dfs3(new_s,ans)
           ans.pop()#回溯
   
   if __name__ == '__main__':
   
       dfs2(s_list,ans)
       print(list(results))
       print(len(results))
   

结果如下：

['cab', 'acb', 'abc', 'bac', 'cba', 'bca']

通过对比分析字符串排列和列表排列的实现方法，尤其是列表排列的三种不同方法（其实就是细微差别，重点是为了突出关于回溯时对上一级原有数据的保护），当看到字符串排列的回溯方法，难以理解为什么代码那么简洁，没有看到回溯的部分，对比下面列表排列的实现，可以发现在递归方法 pailie(s, temp) 中，每次重新调用 paile()方法时， s 都是一个新的对象，与原来的对象是相互独立的，temp 也是如此，因为是字符串类型，所以简单的相加（temp+s[i]）之后就是一个新的字符串。

在列表排列的三种方法中，dfs2()方法的设计思路是和 pailie() 方法一致的，按照深度优先搜索一层一层查找的思路，都是为了让传入的参数对象与上一层被使用的对象相互独立开来。在 dfs() 和 dfs3() 方法中，因为传入的参数对象有列表类型（列表是可变数据类型），所以如果不做 s_list.insert(i,x) 或 ans.pop() 回溯处理，输出结果就会变为['abccbbac', 'abc', 'abccbbaccacab', 'abccb', 'abccbbacca', 'abccbbaccacabba']，究其原因是因为参数对象（列表类型）将每次试探的结果都保存了下来，没有及时做恢复操作。

总结

关于回溯方法解空间的判断，多做练习，记住规律。回溯具体实现方法，主要是回溯点的处理，可以参考列表全排列的实现案例进行理解。

关于其他运用到回溯法的经典案例，后期会一一更新。

Python 回溯法 子集树模块系列——八皇后问题