简单的说,拉格朗日乘子法是一种寻找多元函数在一组等式约束下极值的方法,通过引入拉格朗日乘子,可以将有 d d d 个变量与 k k k 个约束条件的最优化问题转化为具有转化为具有 d + k d+k d+k 个变量的无约束优化问题求解。 而KKT条件和对偶问题则可以看作是拉格朗日乘子法的推广。
目录
- 一、约束优化问题分类
- 1.1 无约束优化
- 1.2 等式约束下的优化问题
- 1.3 不等式约束下的优化问题
- 二、等式约束与拉格朗日乘子法
- 三、拉格朗日乘子法的推广:KKT条件
- 四、拉格朗日原问题与对偶问题
- 4.1 原始问题
- 4.2 广义拉格朗日函数
- 4.3 广义拉格朗日函数的极小极大值问题
- 4.4 原始问题的对偶问题
- 4.5 关于原始问题与对偶问题关系的探讨
- 五、更多资源下载
一、约束优化问题分类
我们根据对优化目标的约束类型可以将该类问题划分为三类:
1.1 无约束优化
m i n f ( x ) min f(x) minf(x)
1.2 等式约束下的优化问题
{ m i n f ( x ) s . t . g i ( x ) = 0 ; i = 1 , . . . , m \left\{\begin{matrix}minf(x)\\s.t.g_{i}(x) = 0 ; i = 1,...,m \end{matrix}\right. {minf(x)s.t.gi(x)=0;i=1,...,m
1.3 不等式约束下的优化问题
{ m i n f ( x ) s . t . g i ( x ) < = 0 ; i = 1 , . . . , m s . t . h i ( x ) = 0 ; i = 1 , . . . , p \left\{\begin{matrix}minf(x)\\s.t.g_{i}(x) <= 0 ; i = 1,...,m \\s.t.h_{i}(x) = 0 ; i = 1,...,p\end{matrix}\right. ⎩⎨⎧minf(x)s.t.gi(x)<=0;i=1,...,ms.t.hi(x)=0;i=1,...,p
对于第一类问题我们可以直接通过求导的方式求解极值;而第二类和第三类问题则可以分别使用拉格朗日乘子法与KKT条件进行求解
二、等式约束与拉格朗日乘子法
对于等式约束下的凸优化问题,我们可以将等式约束 g i ( x ) g_{i}(x) gi(x) 用一个系数 λ \lambda λ 与目标函数 f ( x ) f(x) f(x) 写成一个等式,称为拉格朗日函数,其系数 λ \lambda λ 称为拉格朗日乘子。通过拉格朗日函数对各个变量(包括拉格朗日乘子)进行求导,令其为零,可以求得候选值集合,然后验证求得最优值。
数学原理与解释如下,对于优化问题
{ m i n f ( x ) s . t . g ( x ) = 0 \left\{\begin{matrix}minf(x)\\s.t.g(x) = 0 \end{matrix}\right. {minf(x)s.t.g(x)=0
我们可以分别画出
f ( x , y ) f(x,y) f(x,y) 的等高线与
g ( x , y ) g(x,y) g(x,y) 这条曲线
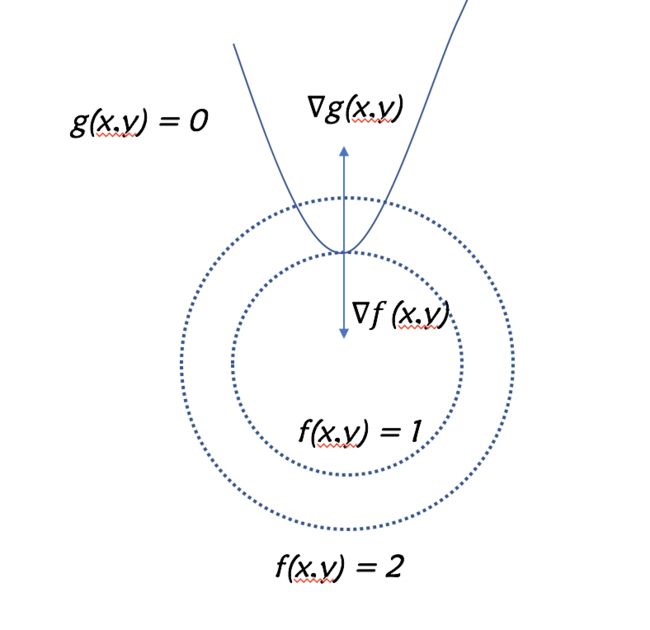
我们的目标是在
g ( x , y ) = 0 g(x,y) = 0 g(x,y)=0 这条曲线上找到一个点使得
f ( x , y ) f(x,y) f(x,y) 的值尽可能的小。不难发现当
f ( x , y ) f(x,y) f(x,y)的等高线与曲线
g ( x , y ) = 0 g(x,y) = 0 g(x,y)=0 相切的时候,目标函数
g ( x , y ) g(x,y) g(x,y) 可以取得最优值,此点两个函数的法向量在同一直线上,必有
λ \lambda λ 使得
▽ f ( x , y ) + λ ▽ g ( x , y ) = 0 \triangledown f(x,y) + \lambda\triangledown g(x,y) = 0 ▽f(x,y)+λ▽g(x,y)=0
可以记为
▽ L ( x , y , λ ) = 0 \triangledown L(x,y,\lambda) = 0 ▽L(x,y,λ)=0
于是我们可以构造函数
L ( x , y , λ ) = f ( x , y ) + λ g ( x , y ) L(x,y,\lambda) =f(x,y) + \lambda g(x,y) L(x,y,λ)=f(x,y)+λg(x,y)
求解它的最优解就等价于求解原带约束的优化问题,而这就是拉格朗日函数
三、拉格朗日乘子法的推广:KKT条件
KKT条件是拉格朗日乘子法的进一步推广,对于具有不等式约束或者等式约束的问题,都可以用它求解。如,对于优化问题
$ \left{\begin{matrix}minf(x)\s.t.g(x) <= 0 \end{matrix}\right. $
我们的目标是在下图的阴影或边界中找到一个点,使得目标函数值最小

最优点
X ∗ X^{*} X∗ 可能在
g ( x ) < 0 g(x) < 0 g(x)<0 的区域中,或在
g ( x ) = 0 g(x) = 0 g(x)=0 上。对于
g ( x ) < 0 g(x) < 0 g(x)<0 的情形,可以看出约束
g ( x ) < = 0 g(x) <= 0 g(x)<=0不起作用,可直接通过求解条件 $\triangledown f(x) = 0 $ 来获得最优点;这等价于将
λ \lambda λ 置零然后对
▽ x L ( x , λ ) \triangledown_{x} L(x,\lambda) ▽xL(x,λ) 置零求解最优点。
g ( x ) = 0 g(x) = 0 g(x)=0的情形类似于上面等式约束的分析,但需注意的是,由于
s . t . g ( x ) < = 0 s.t.g(x) <= 0 s.t.g(x)<=0的限制,此时最优点处的 $\triangledown f(x) $ 的方向必与最优点处的
▽ g ( x ∗ ) \triangledown g(x^{*}) ▽g(x∗)相反,即存在常数
λ > 0 \lambda > 0 λ>0 使得
f ( x , y ) + λ g ( x , y ) = 0 f(x,y) + \lambda g(x,y) = 0 f(x,y)+λg(x,y)=0 。
综上所述,在约束 $g(x) <= 0 $下,最小化
f ( x ) f(x) f(x),可转化为如下约束下最小化目标的拉格朗日函数
{ g ( x ∗ ) < = 0 λ > = 0 λ g ( x ∗ ) = 0 \left\{\begin{matrix}g(x^{*}) <= 0\\ \lambda >= 0 \\ \lambda g(x^{*})=0 \end{matrix}\right. ⎩⎨⎧g(x∗)<=0λ>=0λg(x∗)=0
上式称为KKT条件
四、拉格朗日原问题与对偶问题
4.1 原始问题
现给出原始优化问题如下
{ m i n w f ( w ) g i < 0 ; i = 1 , . . . , k h i ( w ) = 0 ; i = 1 , . . . , l \left\{\begin{matrix} min_{w} f(w)\\ g_{i} < 0 ;i = 1,...,k \\ h_{i} (w) = 0 ; i = 1,...,l\end{matrix}\right. ⎩⎨⎧minwf(w)gi<0;i=1,...,khi(w)=0;i=1,...,l
4.2 广义拉格朗日函数
由原始问题,我们写出一般化的拉格朗日公式
L ( w , α , β ) = f ( w ) + ∑ i = 1 k a i g i ( w ) + ∑ i = 1 l β i h i ( w ) L(w,\alpha,\beta ) = f(w) + \sum_{i = 1}^{k} a_{i}g_{i}(w) + \sum_{i = 1}^{l}\beta_{i}h_{i}(w) L(w,α,β)=f(w)+∑i=1kaigi(w)+∑i=1lβihi(w)
现在设置如下函数(注意这个函数为我们构造的函数):
Θ p ( w ) = m a x α , β : α i > 0 L ( w , α , β ) \Theta _{p}(w) = max_{\alpha ,\beta:\alpha _{i} >0} L(w,\alpha ,\beta ) Θp(w)=maxα,β:αi>0L(w,α,β)
即:
Θ p = m a x α , β : α i > 0 L ( w , α , β ) = m a x α , β : α i > 0 ( f ( w ) + ∑ i = 1 k a i g i ( w ) + ∑ i = 1 l β i h i ( w ) ) \Theta _{p} = max_{\alpha ,\beta:\alpha _{i} >0} L(w,\alpha,\beta) = max_{\alpha ,\beta:\alpha _{i} >0} (f(w) + \sum_{i = 1}^{k} a_{i}g_{i}(w) + \sum_{i = 1}^{l}\beta_{i}h_{i}(w) ) Θp=maxα,β:αi>0L(w,α,β)=maxα,β:αi>0(f(w)+∑i=1kaigi(w)+∑i=1lβihi(w))
对于上述构造的函数,如果满足原始问题的如下约束
{ g i < 0 ; i = 1 , . . . , k h i ( w ) = 0 ; i = 1 , . . . , l \left\{\begin{matrix} g_{i} < 0 ;i = 1,...,k \\ h_{i} (w) = 0 ; i = 1,...,l\end{matrix}\right. {gi<0;i=1,...,khi(w)=0;i=1,...,l
根据KKT条件,有
Θ p = f ( x ) \Theta _{p} = f(x) Θp=f(x);如果上述条件不满足,我们总可以调整
α i \alpha_{i} αi 和
β i \beta_{i} βi使得最大值出现正无穷。因此,可分情况为
Θ p ( w ) = { f ( w ) ( i f w − s a t i s f i e d − p r i m a l − c o n s t r a i n t s ) ∞ ( o t h e r w i s e ) \Theta _{p}(w) = \left\{\begin{matrix} f(w ) (if w -satisfied-primal-constraints)\\ \infty (otherwise) \end{matrix}\right. Θp(w)={f(w)(ifw−satisfied−primal−constraints)∞(otherwise)
4.3 广义拉格朗日函数的极小极大值问题
对于上一小节我们构造的函数 Θ p ( w ) \Theta _{p}(w) Θp(w) , 我们发现当它满足原始问题的限制时,它其实是与原始目标方程 f ( x ) f(x) f(x) 是等价的。因此,如果同样的,我们对 Θ p ( w ) \Theta _{p}(w) Θp(w)求极小值,即
m i n Θ p ( w ) = m i n m a x α , β : α i > 0 L ( w , α , β ) min \Theta _{p}(w) = min max_{\alpha ,\beta:\alpha _{i} >0} L(w,\alpha ,\beta ) minΘp(w)=minmaxα,β:αi>0L(w,α,β)
则,上式的解与原始问题的解是等价的。该形式称为广义拉格朗日函数的极小极大值问题,我们通过上面那么多的推导,其实就是为了
将原始问题转化为等价的广义拉格朗日函数的极小极大值问题
4.4 原始问题的对偶问题
将原始问题写成极小极大值形式以后,我们就可以很方便的写出它的对偶形式,即交换式子中的求极值符号
m a x α , β m i n L ( w , α , β ) max_{\alpha ,\beta} min L(w,\alpha ,\beta ) maxα,βminL(w,α,β)
s . t : α i > 0 , i = 1 , . . , k s.t :\alpha _{i} >0 ,i = 1,..,k s.t:αi>0,i=1,..,k
我们称上式为原始问题的对偶问题
4.5 关于原始问题与对偶问题关系的探讨
当愿问题与对偶问题都取得最优值时,我们有如下结论:
m a x α , β m i n L ( w , α , β ) < = m i n m a x α , β : α i > 0 L ( w , α , β ) max_{\alpha ,\beta} min L(w,\alpha ,\beta ) < = min max_{\alpha ,\beta:\alpha _{i} >0} L(w,\alpha ,\beta ) maxα,βminL(w,α,β)<=minmaxα,β:αi>0L(w,α,β)
即
对偶问题给出了原始问题解的下确界。证明也非常简单
对于任意的
α , β , w \alpha,\beta,w α,β,w 我们有
m i n w L ( w , α , β ) < = L ( w , α , β ) < = m a x α , β : α i > 0 L ( w , α , β ) min_{w} L(w,\alpha,\beta) <= L(w,\alpha ,\beta ) <=max_{\alpha ,\beta:\alpha _{i} >0} L(w,\alpha ,\beta ) minwL(w,α,β)<=L(w,α,β)<=maxα,β:αi>0L(w,α,β)
由于原始问题和对偶问题均有最优解,所以
m i n w L ( w , α , β ) < = m a x α , β : α i > 0 L ( w , α , β ) min_{w} L(w,\alpha,\beta) <= max_{\alpha ,\beta:\alpha _{i} >0} L(w,\alpha ,\beta ) minwL(w,α,β)<=maxα,β:αi>0L(w,α,β)
即
d ∗ = m a x α , β : α i > 0 m i n w L ( w , α , β ) < = m i n w m a x α , β : α i > 0 L ( w , α , β ) = p ∗ d^{*} = max_{\alpha ,\beta:\alpha _{i} >0} min_{w} L(w,\alpha,\beta) <= min_{w} max_{\alpha ,\beta:\alpha _{i} >0} L(w,\alpha ,\beta ) = p^{*} d∗=maxα,β:αi>0minwL(w,α,β)<=minwmaxα,β:αi>0L(w,α,β)=p∗
当
d ∗ < p ∗ d^{*} < p^{*} d∗<p∗ 时这种关系称为“弱对偶性“;若
d ∗ = p ∗ d^{*} = p^{*} d∗=p∗时,则称为“强对偶性“,此时对偶问题能够获得原始问题的最优下界。对于一般的优化问题,强对偶性通常不成立,但是,若原始问题为凸优化问题且其可行域中至少有一点使得不等式约束严格成立,则此时强对偶性成立。这里要说明的是,
不论原问题凸性如何,对偶问题始终为凸优化问题。在强对偶性成立时,通过求解对偶问题可以解决主问题
KKT条件是原始问题与对偶问题有解的充分必要条件, 拉格朗日对偶问题完整的KKT条件如下
(1)
▽ w L ( w ∗ , α ∗ , β ∗ ) = 0 \triangledown_{w} L(w^{*},\alpha^{*},\beta^{*}) = 0 ▽wL(w∗,α∗,β∗)=0
(2)
▽ α L ( w ∗ , α ∗ , β ∗ ) = 0 \triangledown_{\alpha} L(w^{*},\alpha^{*},\beta^{*}) = 0 ▽αL(w∗,α∗,β∗)=0
(3)
▽ β L ( w ∗ , α ∗ , β ∗ ) = 0 \triangledown_{\beta} L(w^{*},\alpha^{*},\beta^{*}) = 0 ▽βL(w∗,α∗,β∗)=0
(4)
α i ∗ g i ( w ∗ ) = 0 ; i = 1 , 2 , . . . , k \alpha_{i}^{*}g_{i}(w^{*}) = 0 ;i = 1,2,...,k αi∗gi(w∗)=0;i=1,2,...,k
(5)
g i ( w ∗ ) < = 0 ; i = 1 , 2 , . . . , k g_{i}(w^{*}) <= 0 ;i = 1,2,...,k gi(w∗)<=0;i=1,2,...,k
(6)
α i ∗ > = 0 ; i = 1 , 2 , . . . , k \alpha_{i}^{*} >= 0 ;i = 1,2,...,k αi∗>=0;i=1,2,...,k
(7)
h ( w ∗ ) > = 0 ; i = 1 , 2 , . . . , j h(w^{*})>= 0 ;i = 1,2,...,j h(w∗)>=0;i=1,2,...,j
特别值得指出的是,式4称为
互补对偶条件,它意为
α \alpha α 与
g ( w ) g(w) g(w)必有一为0
五、更多资源下载
微信搜索“老和山算法指南”获取更多下载链接与技术交流群

有问题可以私信博主,点赞关注的一般都会回复,一起努力,谢谢支持。


![]()