union-find算法(路径压缩+加权quick-union算法 数组实现)

算法第四版曾提过,通过路径压缩实现几乎（注意几乎)完全扁平化的树，为何我要说注意几乎,因为书作者数据给的好,我通过实现发现利用
书中数据

自己将结果画图发现和加权quick-union效果一样,然后我检查代码,又上网查找发现代码没错,原来是我理解有误,错误就在几乎这两个字上

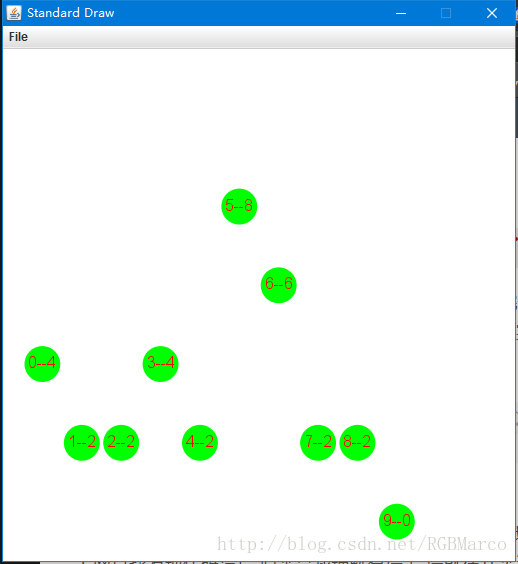
注意这图和我上篇博文中的加权quick-union效果一样（上篇博文入口），按照我的错误理解效果应该是除了6–6其他都在一排的，应为他们是一个连通分量，应该让他们都指向根节点,这样当然可以,通过一个for循环就可以,不过这样一下又回到解放前(甚至还倒退在quick-find算法的基础倒退),那路径·压缩是干嘛的呢？？的确是用来将一颗子树节点练到根节点上,不过这种是具有概率性的，因为连通性的点只能指向他的前一个点，则当这个点是中间的点就尴尬了,你从find(p)给定的点只能向上遍历，将前驱连到根节点，可是p的子节点就无缘了，如果后面操作没有针对p的子节点，那恐怕只有认命了

下面给出 路径压缩 + 加权quick-union算法实现(数据和结果以上已给出)

import edu.princeton.cs.algs4.StdDraw;
import edu.princeton.cs.algs4.StdOut;

public class UF {
    private int[] id;
    private int[] sd;
    private int count;
    public UF(int N)
    {
        id = new int[N];
        sd = new int[N];
        for (int i = 0; i < N; ++i)
        {
            id[i] = i;
            sd[i] = 1;
        }
        count = N;
    }
    public boolean connect(int p,int q)
    {
        return find(p) == find(q);
    }
    public int find(int p)
    {
        while (id[p] != p)
        {
            id[p] = id[id[p]];
            p = id[p];
        }
        return p;
    }
    public void union(int p,int q)
    {
        int l = find(p);
        int r = find(q);
        if (l == r) return;
        if (sd[l] > sd[r])
        {
            id[r] = l;
            sd[l] += sd[r];
        }
        else
        {
            id[l] = r;
            sd[r] += sd[l];
        }
        --count;
    }
    public int count()
    {
        return count;
    }
    public void display()
    {
        for (int i = 0; i < id.length; ++i)
            StdOut.println(i + "--" + id[i]);
    }
    public void draw()
    {
        StdDraw.setXscale(-1,id.length + 2);
        StdDraw.setYscale(-1,id.length + 2);
        StdDraw.setPenRadius(0.07);
        for (int i = 0; i < id.length; ++i)
        {
            StdDraw.setPenColor(StdDraw.GREEN);
            StdDraw.point(i, id[i]);
            StdDraw.setPenColor(StdDraw.RED);
            StdDraw.text(i,id[i],Integer.toString(i)+ "--" + Integer.toString(id[i]));
        }
    }
}

main.java

import edu.princeton.cs.algs4.In;

public class Main {
    public static void main(String[] args)
    {
        UF uf = new UF(10);
        In in = new In("test.txt");
        while (!in.isEmpty())
        {
            int l = in.readInt();
            int r = in.readInt();
            uf.union(l, r);
        }
        uf.display();
        uf.draw();
    }
}